时间序列的分频与建模

田 甜，李星野

(上海理工大学 管理学院，上海 200093)

0 引言

时间序列建模方法的产生最早可追溯到1927年，英国统计学家Yule(1871～1951)提出自回归(Auto-Regressive,AR)模型。1931年，英国数学家、天文学家Walker爵士在分析印度天气规律时使用了移动平均(Moving Average,MA)模型和自回归移动平均 (Auto-Regressive Moving Average,ARMA)模型。这些模型奠定了时间序列建模方法的基础。1970年，美国统计学家Box和英国统计学家Jenkins在总结前人研究的基础上，系统地阐述了对求和自回归移动平均(Auto-Regressive Integrated Moving Average,ARIMA)模型的识别、估计、检验及预测的原理与方法，这些是经典的时间序列建模方法。近20年，统计学家纷纷转向多变量场合、异方差场合和非线性场合的时间序列分析方法的研究。

文献[1]提出了一种基于支持向量回归(Support Vector Regression,SVR)和独立成分分析 (Independent Component Analysis,ICA)的综合金融时间序列预测模型，该建模方法运用SVR对通过ICA去噪后的预测变量建立预测模型。经过本方法与SVR和随机游动模型的比较，实验结果表示本方法能降低预测误差，提高预测精度，具有更好的预测效果。文献[2]通过前馈神经网络(Feedforward Neural Network,FNN)，ARIMA与FNN的混合模型[3]，自我激励门限自回归模型(Self-Exciting Threshold Auto-Regressive Model,SETAR)[4]和该文献提出的ARIMA与Elman回归神经网络 (Elman's Recurrent Neural Networks,ERNN)混合模型的方法分别对加拿大猞猁相关数据进行预测，结果表明使用该方法所得均方误差最小，预测效果最好。而文献[5]则对上证指数A股日收益指数的波动性建模，介绍并使用了非参数模型设定检验方法进行多个模型的评价,文献[6]则分析和比较了时间序列的数据挖掘思想与经典建模法的基本思路，总结各自的优缺点，并阐述二者在本质上是不同的两类重要的时间序列分析法。随着小波变换和傅里叶变换的应用越来越广泛，信号处理中的时频分析逐渐被沿用到时序分析中，文献[7]将小波多分辨率分析引入协整建模理论,提出多分辨协整和多分辨误差校正模型。文献[8]将小波分析和ARMA模型引入时间序列数据挖掘中，利用小波消噪对原始时间序列进行滤波，并应用小波变换挖掘和分离金融时间序列的各种隐周期和非线性。

本文采用分频方式分析时间序列并为时间序列建模，是一种基于数字信号处理和现代时间序列分析的方法。由于时间序列的低频分量反映出长记忆特性，难以直接用时滞自相关模型建模，因此本文首先对时间序列做离散余弦变换，用低频变换系数重构出时间序列的低频分量，这相当于对时间序列进行一次理想低通滤波，此时的低频分量就是为数不多的几个余弦函数的线性组合，结构非常简单，而剩余的高频部分则比较好地满足时滞自相关模型的建模条件。为了减少自回归模型的建模计算量，加快建模速度，所以本文借鉴了ARMA模型的自相关理念，直接采用时滞自相关分析方法确定模型结构，而不是像ARMA模型那样通过自相关系数和偏自相关系数的拖尾截尾性定阶的过程。针对股票多年日收盘价所作仿真试验证明该时间序列建模方法是有效的，模型比较好地刻画了时间序列的变化规律。

1 时间序列的分频与建模

1.1 离散余弦变换

在频谱分析和各种滤波方法中，最基本的数学工具是Fourier分析。离散余弦变换是一种与Fourier变换紧密相关的数学运算，它是Fourier变换的实数域变换，避免了复数运算，这是它优于Fourier变换之处。

离散余弦变换（Discrete Cosine Transform,DCT）的形式如

DCT相应地由有限长序列构造出一个周期的对称序列，由此可唯一地恢复原有限长序列。因为这样做有许多方式，所以DCT有多种定义。对于实序列这些变换构成了一族含有16种形式的正交归一化变换。这些变换中最常使用的是DCT-1和DCT-2表示式，本文中应用的是DCT-2表示式，所以主要针对它做介绍。

不同形式DCT的各种周期延拓均可看作是N点序列±x[n]和±x[-n]平移复本的和。对于DCT-2，x[n]延拓为周期为2N的周期序列，用下式表示：

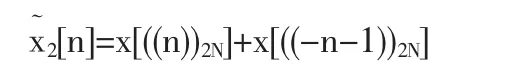
由于序列的端点没有重叠，所以不需要对它们进行调整，以保证当n=0，1，…，N-1时x[n]=。这种对称性称为二型周期对称。在这种情况下周期序列关于“半样本”点等为偶周期对称。DCT-2定义为如下变换：

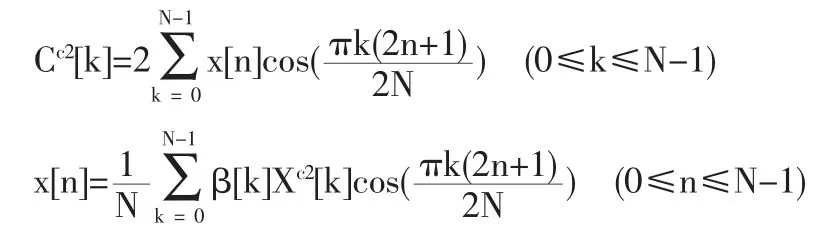
式中DCT-2反变换用到权函数

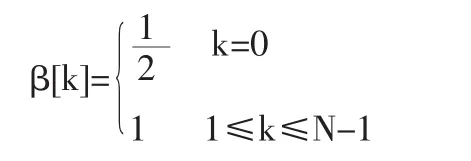
在许多处理中，DCT定义包括使该变换成为单式的归一化因子。例如，DCT-2通常定义为

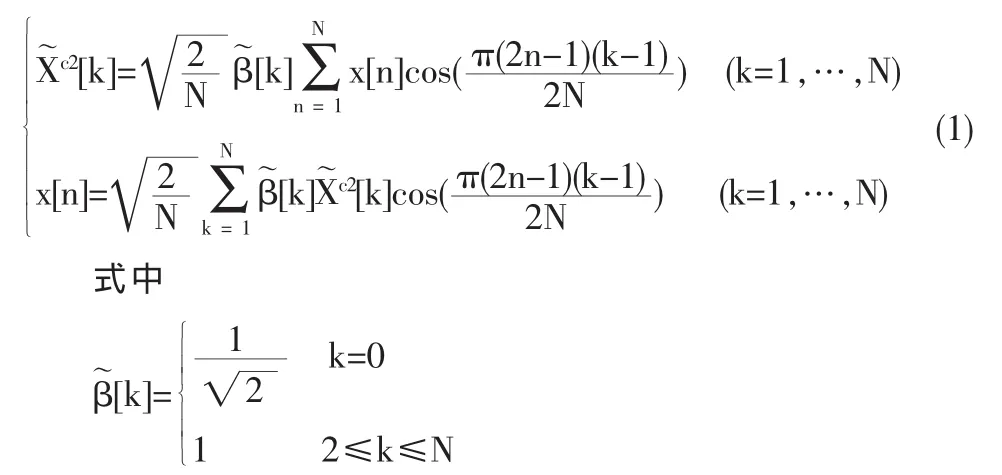
将上式与前一组表达式进行比较，可知乘积因子2，1/N和β[k]在正、反变换式中处于不同的位置。

1.2 时滞自相关模型

ARMA时间序列模型的理论已发展得比较成熟，它是将平稳时间序列利用自回归过程和移动平均过程，以及样本自相关系数、样本偏相关系数等数据，对模型进行辩识、估计和预报。但ARMA模型拟合是要根据样本自相关系数和偏自相关系数的性质估计自相关阶数和移动平均阶数的，这种定阶过程过于繁琐，为了提高建模效率，本文直接采用时滞自相关分析方法确定时间序列高频分量的模型结构，而不是通过自相关系数和偏自相关系数的拖尾截尾性确定模型结构。

ARIMA模型则是通过对具有趋势的时间序列差分，使之成为平稳随机序列，然后再用此平稳时间序列去描述这一随机过程的建模方法，由于本文原始时间序列经过离散余弦变换后已去除了趋势波动，所以无需使用ARIMA模型的建模方法。

时滞自相关模型描述了时间序列x'[n]某一时刻n和其前p个时刻序列值之间的相互关系，通过比较时刻n和其前p个时刻序列值的相关系数，提取相关系数较大的若干项作为时滞自相关变量x[n-p]，然后可运用多元线性回归算出各变量x[n-p]的待定系数φ[p]和独立误差项ε，最后时间序列x'[n]便能通过下式建立时滞自相关模型：

1.3 综合模型的建立

综合（1）式和（2）式可得时间序列分频建模的模型表达式为：

2 实验分析

时间序列的时滞自相关分析已在经济数据分析、控制系统设计等科学领域得到了广泛的应用并取得了良好的效果。本文在这一部分将通过运用离散余弦变换对股票九年日收盘价进行分频处理，建立针对低频平滑部分的余弦重构模型和针对高频波动部分的时滞自相关模型，再将两者叠加便可对原始数据的变化情况进行拟合。

时间序列经过离散余弦变换后，将把数据的高频分量集中在中间，而低频分量集中在数据两端。对导入的原始数据提取高频分量，并对其做时滞自相关分析，如图1所示。

从图1可知，若取置信区间为(-0.2210，0.2210)，则可选定p=2，p=3和p=6时φ取非零值，其余φ系数的值皆为零。再通过对 x[n]，x[n-2]，x[n-3]和 x[n-6]序列进行线性回归分析，可求得 φ[2]=-0.4838，φ[3]=-0.2240，φ[6]=0.2204 与 ε=-0.0002。

剩下的低频分量则选用余弦函数重构。数据经过离散余弦变换后的序列展示了能量分布情况，数值平方大的项能量高，数值平方小的项能量低。实际操作时可选出十项左右，使它们的平方和占所有低频分量离散余弦变换系数平方和的95%以上，则基本可以用这几项来代表所有低频的波动情况。

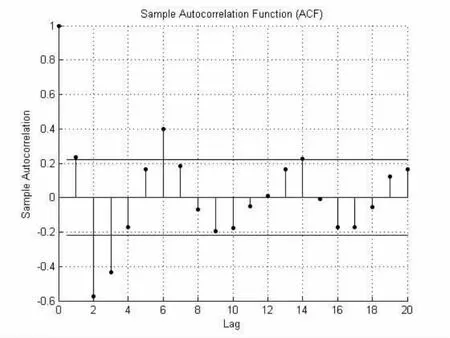
图1 数据高频分量的时滞自相关系数图

通过编程计算，由于原始序列经离散余弦变换所得的低频分量中的第1,2,3,4,5,6,8,10,12,15,17项的能量和占整个低频分量总能量的95%以上，所以取k=1,2,3,4,5,6,8,10,12,15,17。

根据以上确定下来的各参数值便可得到原时间序列的数学模型表达式为：

运用该模型对股票多年日收盘价做仿真试验并和原时间序列进行比较，如图2所示。

较光滑的曲线为模拟出的结果，原序列与模拟序列差的绝对值的平均数为1.2078，标准差为1.7586。从图2中可以看到，除原时间序列突变值的模拟结果不够精确以外，其它部分模拟情况良好，所建模型可以基本反映原时间序列的变化趋势。

综合以上实验操作，可将时间序列分频建模的过程总结为以下几个步骤：

(1)对原时间序列进行离散余弦变换，分别提取变换系数序列当中的高频分量和两端的低频分量。

(2)选取高频分量中与当前时刻序列值相关系数较大的过去若干时刻的序列值作为时滞自相关变量，然后利用线性回归分析求出相关系数，并建立高频分量的时滞自相关模型。

(3)提取低频分量中能量较大的若干项重构时间序列平滑部分的波动情况，并建立低频分量的反离散余弦变换模型。

(4)叠加高、低频分量的模型，得到综合模型。

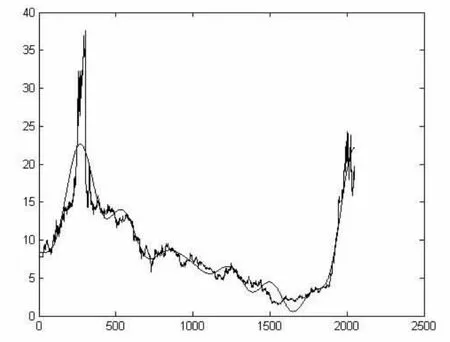
图2 原时间序列与模拟结果的比较图

3 结论

由于时间序列的低频分量反映出时间序列相对长期的变化规律，难以直接使用时滞自相关模型建模，因此本文先对时间序列做离散余弦变换，用低频变换系数重构出时间序列的低频分量，这相当于对时间序列进行一次理想低通滤波，此时的低频分量就是为数不多的几个余弦函数的线性组合，结构非常简单，而剩余的高频部分则比较好地满足时滞自相关模型的建模条件。

时滞自相关模型借鉴了ARMA模型建模方法中的自相关理念，但未采用ARMA模型根据样本自相关系数和偏自相关系数的拖尾截尾性估计自相关阶数和移动平均阶数的定阶过程，因为此定阶方式过于繁琐，从而时滞自相关分析方法可减少建模计算量，加快建模速度。针对股票多年日收盘价所作仿真试验证明该时间序列建模方法是有效的，模型比较好地刻画了时间序列的变化规律。

[1]Lu C J,Lee T S,Chiu C C.Financial Time Series Forecasting Using Independent Component Analysis and Support Vector Regression[J].Decision Support Systems,2009,(47).

[2]Aladag C H,Egrioglu E,Kadilar C.Forecasting Nonlinear Time Series with a Hybrid Methodology[J].Applied Mathematics Letters,2009,(22).

[3]Zhang G.Time Series Forecasting Using a Hybrid ARIMA and Neural Network Model[J].Neurocomputing,2003,(50).

[4]Katijani Y,Hipel W K,Mcleod A I.Forecasting Nonlinear Time Series with Feed-forward Neural Networks:A Case Study of Canadian Lynx Data[J].Journal of Forecasting,2005，(24).

[5]李成群.基于非参数模型设定检验方法的上证指数波动率的研究[J].学术论坛,2007，(9).

[6]胡桔州,兰秋军.金融时间序列的数据挖掘技术与经典统计模型的比较[J].系统工程,2005,23(6).

[7]许启发,蒋翠侠,张世英.基于小波多分辨分析的协整建模理论与方法的扩展[J].统计研究,2007,24(8).

[8]佟伟民,李一军,单永正.基于小波分析的时间序列数据挖掘[J].计算机工程,2008,34(1).