一种新颖的概率仿真优化方法

蔡奎生

（苏州经贸职业技术学院，江苏 苏州 215000）

仿真优化就是在现代先进优化理论的基础上，采用计算机仿真技术来获得待研究系统的一种较为优化的决策[1]。仿真优化已广泛地应用到各个领域，如自动控制、系统设计和仿真算法优化等[2～4]。 目前较为常用的仿真优化方法有[5～8]：随机优化方法、基于梯度的方法、响应曲面法及智能优化方法。这些仿真优化方法已被广泛地应用于诸多领域，如生产制造系统[9]、经济系统[10]。

1 概率仿真优化方法

1.1 仿真重复次数的确定方法

对于大多数实际的仿真优化问题来讲，点xk处的响应值不等同于它的适应度值F(xk)，所以需要在点xk处进行多次仿真。在本文中，假设在点xk处进行p次仿真试验，则多次仿真取平均值的计算方式如下：

这里，笔者采用以下方式来确定p的取值：

其中，pi表示在试验点Xi处需要进行重复仿真试验的次数，m表示一个固定的参数，||·||表示计算向量的模，Xi表示第i个个体，X*表示当前种群中的最优个体。

1.2 两个个体的优劣比较

在公式(1)中，除非p的取值非常接近于正无穷，否则使用R(xk)来替代f(xk,w)都是不合适的。所以，很难采用一种精确的方法来比较R(xk)和R(xk+1)。笔者采用假设检验方法来尝试构造判断两个个体优劣的方法。可构造以下假设：

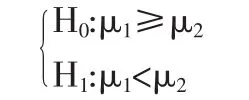
其中，R(x1)和R(xw)分别表示点x1和 x2处所得到的平均响应值，μ1和μ2分别表示点x1和x2处的实际适应值。这样就可在给定检验水平α下基于统计量R(x1)和R(x2)来对上述假设检验做出判断。如果上述假设被拒绝，则μ1＜μ2，说明染色体以1-α的置信水平水平优于染色体x1。

1.3 多个个体的优劣排序

设X1,X2,…,Xn分别表示当前种群中的n个个体；μ1,μ2…,μn分别表示这 n个个体的实际应值；R(x1),Rx2),…,R(xn)分别表示这n个个体的平均适应值。这里，可采用下面的思路来对n个个体的进行排序：先找出所有n个个体中实际适应度值最大的那个个体(具体方法参见1.2节)，从原队列中去掉该个体，将该个体排在新队列中的首位；依次类推，直到原来队列中的个体数目为零时排序结束。

2 量化正交遗传算法

本文定义染色体x=(x1,x2,…,XN)的成本为f(x)。全局优化问题等价于找到成本最小的染色体。

2.1 初始种群的生成

在求解全局优化问题前，我们不知道全局优化点位于哪个区域。因而就希望优化算法从一开始就在可行解空间中进行均匀地、离散地搜索，以至于算法可以均匀地搜索整个可行解空间。不难发现，正交表在所有可能的组合中指定了均匀离散分布的数量规模比较小的组合群。所以，正交设计方法是能产生一组比较好的初始种群的潜在的方法。定义第i个自变量为xi，因而每个染色体有N个自变量。这些自变量都是连续的，但正交设计方法仅仅针对于处理那些离散的自变量。为了克服这个缺点，我们将每个自变量都量化成有限的值。本文将自变量xi的定义域[li,ui]量化成Q1个水平ai1,ai2,…aiQ1，这里的Qa是奇数，具体的aij计算公式如下：

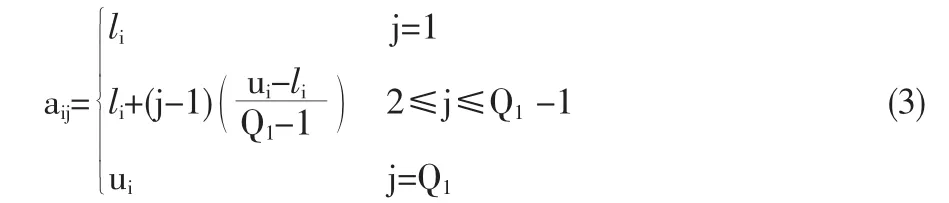
为方便起见，称aij为第i个自变量的第j个水平，定义ai=(ai1,ai2,…,a1Q1)。完成自变量的量化操作以后，自变量x1拥有Q1个可能水平ai1,ai2,…,aiQ1，然后可行解空间包含个点。本文采用正交设计的方法在可行解空间中选择一小群样本点。

首先构建一个合适的正交表。如前所述，前面的构造正交表的方法仅能构造正交表LM1()，此处的M1=，J1是满足以下条件的正整数：

当可行解空间比较大时，这种方法很可能生成收敛性比较好的初始点。然而，M1值的大小依赖于N和Q1的大小，不能任意地增大。为了解决这个问题，将可行解空间分解成S个部分，这里的S是一个设计参数。将s维区间[l,u]分解成为以下 S 个部分：[l(1),u(1)]，[l(2),u(2)]，…，[l(s),u(s)]，这里

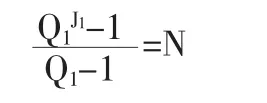
由于优化问题的维数N是给定的，因而可能不存在满足上式的Q1和J1。我们可以将上面的要求放宽一些，选择满足下列条件的最小的正整数J1：

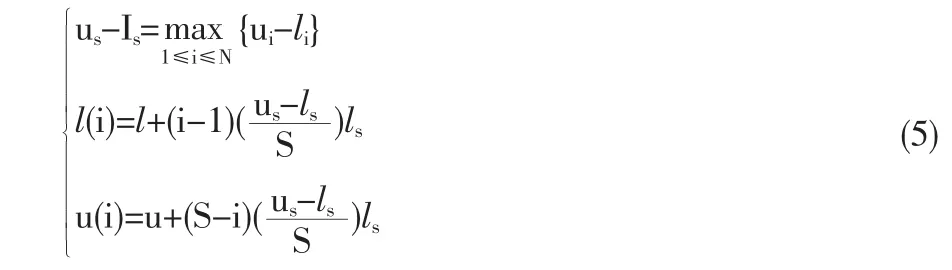
其中，i=1，2，…，S；ls是诸如第 s个元素为 1 其他元素为0的一个N维向量。我们应用正交表LM1()在每一个部分都生成M1个染色体，这样我们总共就得到了M1S个潜在的染色体。我们从中选择G个代价最小的初始种群染色体。

2.2 量化的正交交叉算子

量化正交交叉算法将父代个体定义的求解空间量化成有限数目点，然后应用正交设计方法选择一群有代表性的规模比较小的潜在子代个体。考虑以下两个父代个体：

将每一个父代求解空间[lparent,upaent]量化成Q2份，这样任意两个连续水平之间的差异是相同的。尤其值得一提的是，我们将第 i维区间量化成 βi1,βi2,，βiQ2，其中：

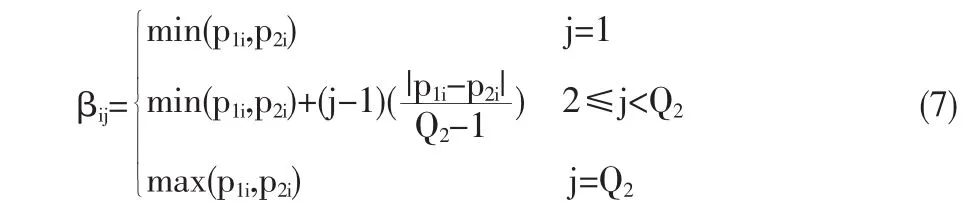
定义 βi=(βi1,βi2,…,βiQ2)。 由于种群的不断进化和改进，种群成员之间越来越接近，两个父代个体定义的求解空间也越来越小。由于Q2是定值，随着量化点的逐步接近，我们就可以得到越来越精确的结果。

在完成求解空间[lparent,upaent]的量化后，应用正交设计方法选择一批数据规模比较小的富有代表性的样本点作为潜在的子代，然后选择一些代价最小的样本点作为子代。为了避免在选择过程中大规模的评价种群点，每一对父代尽可能不要产生太多的潜在子代点。基于这个目的，将变量x1,x2,…,xN分成F组，这里的F是一个很小的设计参数。每一组将会被看成一个因素。这样，相应正交表的组合数目将会减少，然后就产生一个规模比较小的初始种群。这里，随机地生成F-1个整数 k1,k2，…,kF-1这里不妨假定 1＜k1＜k2＜…＜kF-1。 然后对于每个染色体x=(x1,x2,…,xN)产生以下F个因素。

因为x1,x2,…,xN可以被量化，我们为第i个因素定义如下Q2各水平：

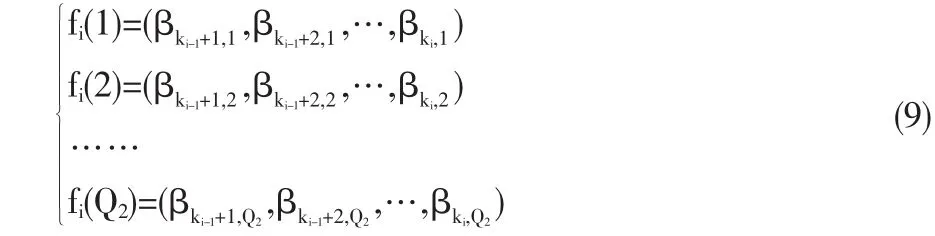
3 二级分销网络系统仿真模型

对于一个确定了分销中心的二级分销网络系统，可以把其看成是一个在分销中心产生库存的库存系统。这个库存系统以分销中心为中心，集成考虑库存和运输。通过控制库存可以实现对整个分销网络进行管理。离散事件系统仿真能够准确记录系统各个环节的状态变化情况，并能根据这些记录得到系统的各个评价指标的统计结果。

3.1 目标和边界

应用仿真技术研究二级分销网络系统的目的是通过各种库存指标比较各种订货策略的优劣，如在不同的需求情况下，何时订货、订多少货为宜，库存安全量如何确定等。二级分销网络系统的优劣常采用“费用(效益)”的高低来衡量，主要的费用有运输费用、订货费用、仓储费用和缺货损失费等。在整个分销系统的不断变化中，引发事件是用户需求的产生和满足，因此把用户需求的产生和满足作为模型的边界。

3.2 实体

二级分销网络系统的实体包括供货方、分销中心、用户和货物。其中，供货方、分销中心和用户为永久实体，货物为临时实体。对于供货方来说，必须满足供应量足够，即不管订货需求何时到达，供货方都能满足分销中心的订货需求；对于用户来说，需求的产生是无条件的，只是在时间上符合某种规律，而与其它因素无关。

3.3 流程分析

在二级分销网络系统中，分销中心库存量的变化是由用户需求和分销中心订货两个方面的因素引起的。由于用户需求使得库存量不断减少，为了保证供应，就需要订货来补充库存量。随着需求和订货的不断发生，库存量呈现动态分布。

3.4 仿真算法

本文采用事件调度法对二级分销网络系统进行仿真。事件是指状态变化的瞬间。事件调度方法以事件为基础，用事件的观点来分析现实系统，它通过定义事件及每个事件的发生对系统状态的影响，按时间顺序确定并执行每个事件发生时有关的逻辑、数学关系。基于事件调度的仿真模型用于描述各类离散事件的发生及相关联的逻辑变换。

在用事件调度法建立模型时，全部事件都放在事件链表中。由时间控制模块从事件链表中选择具有最早发生时间的事件，并将仿真时钟修改到该事件发生的时刻，再调用与该事件相应的事件处理模块和动画图像描绘模块，这样，事件的选择与处理不断地进行，直到仿真终止条件得到满足或终止事件发生为止。

4 实证分析

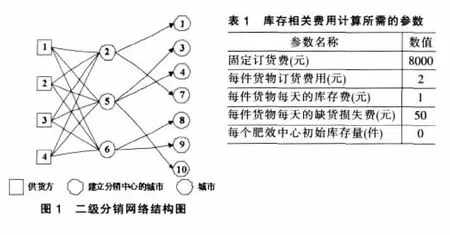
某公司已经对分销网络进行了设计，如图1所示。本部分通过分析历史数据得到用户需求产生的时间分布的基础上，通过系统仿真从而得到最优的订货策略。

4.1 基本设置

笔者采用Arena软件自带的Input Analyzer功能对历史数据进行分析，得到用户的需求达到的时间间隔服从参数为λ(λ1=42,λ3=45,λ4=22,λ7=60,λ8=55,λ9=26,λ10=39)的泊松分布。通过分析，确定计算库存相关费用所需的参数如表1所示。

笔者采用定期定量订货方式，三个分销中心分别采用每周订货1000件或5000件。仿真系统模拟所有的8种组合，从中选取最优的订货策略。编号为2、5、6的分销中心分别按照自己的订货策略发出自己的订单，然后比较与编号为1、2、3、4的供货方的距离，从中选择距离最近的供货方供货。为了计算方便，这里假设供货方的供应量不受限制。记录其中产生的订货费、运输费和库存量增加。编号为1、3、4、7、8、9、10的用户按照相应的泊松分布产生自己的需求，分别把订单发给相应的分销中心。若分销中心可以满足订单所需货量则发货，否则产生缺货。记录其中发生的运输费用、仓储费用和缺货损失费用。

4.2 实验结果

仿真时间设为1年，仿真得到各种订货策略下的费用见表2。在表2中，用“1”表示采用每周订货1000件的订货策略，用“2”表示每月订货5000件的订货策略。例如：表2中最后一行的订货策略为分销中心2每月订货5000件，分销中心5每周订货1000件，分销中心6每月订货5000件。

通过比较，可以得到使这个二级分销网络系统总费用最少的订货策略为:分销中心2每周订货1000件，分销中心5每月订货5000件，分销中心6每月订货5000件，其费用为27415436元。

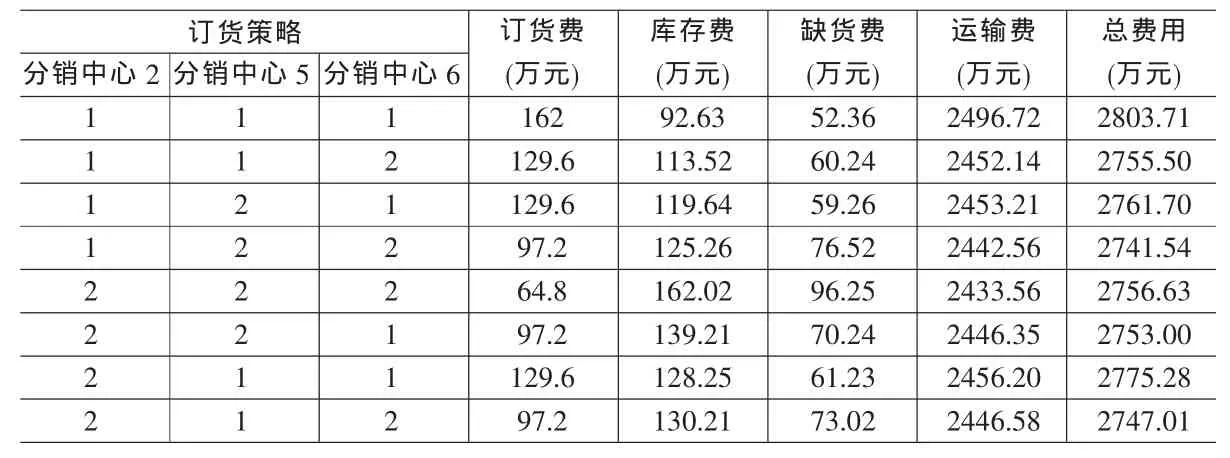
表2 各种订货策略下的费用表

5 结束语

本文的主要创新点是：提出了一种将计算机仿真技术、遗传算法和假设检验等完美地结合的概率仿真优化方法。在二级分销网络系统的实证研究表明，采用本文方法能获得比较满意的优化结果。

[1]Cao X R,Ho X C.Estimation of Co-Join Time Sensitivity in Queuing Networks Using Perturbation Analysis[J].Journal of Optimization Theory and Applications,1997,44(3).

[2]Olsder G J.On the Characteristics Equation and Minimal Realizations for Discrete-Event Dynamic System[J].Analysis and Optimization of Systems,1998,83.

[3]Azadivar,F.A Tutorial on Simulation Optimization[C].In Proceedings of the 1992 Winter Simulation Conference,1992.

[4]Fu,M.C.Optimization Via Simulation:A Review[J].Annals of Operational Research,1994,(53).

[5]Rosenblatt,M.J.,Roll,Y.,Zyse,V.A Combined Optimization and Simulation Approach for Designing Automated Storage/Retrieval Systems[J].IIE Transactions,1993,25(1).

[6]Kleijnen,J.P.C.Simulation and Optimization Production Planning:A Case Study[J].Research Memorandum,1988.

[7]G.V.Reklaitis,A.Ravindran,K.M.Ragsdell.Engineering Optimization:Methods and Applications[M].New York：John Wiley&Sons,1983.

[8]R.Fletcher.Practical Methods for Optimization(2ndEdition)[M].New York：John Wiley&Sons.1987.

[9]P.E.Gill,W.Murray,M.H.Wright,Practical Optimization[M].London,Academic Press,1981.

[10]A.M.Law,W.D.Kelton,Simulation Modeling and Analysis[M].New York:McGraw-Hill,2000.