事业编制规模的预测方法

彭 峰，邓群钊

（南昌大学 理学院，南昌 330031）

0 引言

近年来，随着我国对事业单位机构编制改革的不断深入，探索如何测算事业编制规模以增强区域编制管理，提高公益服务水平，促进社会经济发展成为重要的研究课题。现有的研究[1，2]分离出影响事业编制规模的主要因素：地区人口、面积、区划、国内生产总值、财政收入和国民收入等，通过分析这些社会经济因素与编制规模之间的联系来确定总量控制目标。用这些方法得出的事业编制规模受到社会经济发展水平制约，具有一定的合理性，但没有从系统角度考虑事业编制规模对社会经济发展的反作用，即事业编制规模通过影响公共事业发展而对区域社会经济发展产生作用。然而，事业编制规模预测的复杂性不仅在于事业编制与社会经济之间的相互影响、相互制约，还在于事业编制随着体制改革不断变化。因此，本文把因子分析、回归分析和马尔可夫预测结合起来，提出了一种测算事业编制规模的新方法。

1 总量预测模型

事业编制规模的变化是社会经济发展和事业体制变革共同作用的结果。选取影响事业编制规模的相关指标，通过因子分析从初始指标体系中找出少数几个因子，考虑到近十几年来体制变革对编制规模的影响，引入虚拟变量，建立事业编制规模与这些因子的线性回归模型，这种模型虽然可以解释变革过程中编制规模和社会经济发展之间的关系，但不能很好地解释实际编制规模的波动现象。因此，结合马尔可夫链对回归预测的残差进行修正，从而建立事业编制规模的组合预测模型。本文把编制规模预测分为三个阶段：选取相关指标，建立基于因子分析的回归模型以及组合预测。

1.1 指标体系选取

影响事业编制规模的指标不仅涉及社会状况、经济条件因素，也包括就业状况、事业投资与发展水平等相关因素。这些因素不仅自身处于不断的发展变化过程中，而且它们之间相互作用，相互影响，相互制约，构成一个复杂的动态系统。在这个系统中，一定的区域社会经济发展水平可以维持相应的事业编制规模，这种编制规模是满足当前公共事业发展所需的一种投入，公共事业的发展水平又会对社会经济发展产生反作用。 鉴于此，本文把事业编制规模影响因素分为两类：反映区域对事业编制供给能力的社会经济指标以及反映公共事业发展水平的行业指标。在选取这些指标时，考虑到科学性、合理性、实用性和易于操作，建立以下指标体系。

（1）反映区域对事业编制供给能力的社会经济指标：年末人口(x1)，国内生产总值(x2)，财政支出(x3)，事业费(x4)，第三产业就业人数(x5)。

（2）反映公共事业发展水平的行业指标[3～5]：科技三项费用(x6)，中等教育在校学生数(x7)，初等教育在校学生数(x8)，电视人口覆盖率(x9)，卫生技术人员(x10)，“三废”综合利用产品产值(x11)。

1.2 含公共因子和虚拟变量的回归模型的建立

由于初始指标之间往往有较强的相关关系，可能会掩盖一些重要信息，也影响对问题的解释能力。因此，采用因子分析从大量原始指标中提炼出反映主要问题的公共因子，用来进一步分析。因子分析模型[6]为：

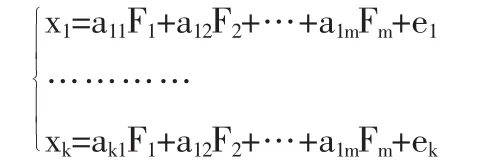
其中，Fj是公共因子；aij是公共因子负载，表示第i个指标在第j个因子上的负载；ei是特殊因子，只与xi有关。设R是标准化数据的相关系数矩阵，则公共因子

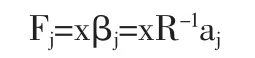
以Fj为变量，建立事业编制规模Y与Fj之间的回归模型，考虑到事业编制规模受政策环境影响很大，近十几年来，事业体制经历了一系列的变革，包括使原生产经营类和行政支持类事业单位逐渐退出了事业编制序列，用一个方程回归可能导致模型结构不稳定，所以采用引入虚拟变量的回归模型，记

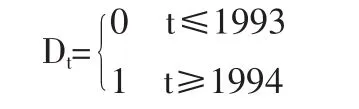
回归方程的具体形式需要通过相关软件对数据分析后得出，为叙述模型方便，暂时记

通过曲线估计第t+1年的因子值Fj,t+1，可以预测第t+1年的事业编制规模Y^t+1。

1.3 马尔可夫链与组合预测

建立线性回归模型后，借助马尔可夫链预测对(1)式得出的预测值进行修正。马尔可夫链预测分为三个步骤[7,8]：划分状态，构造状态转移概率矩阵，确定预测值。

(1)划分状态

根据各年残差大小，按近似等概率将残差值{e1,e2,…，en}分为 s(s 可合适选取) 个状态，记为 Ei∈[Ei-,Ei+]，i=1,2,…，s。

(2)构造状态转移概率矩阵

若Mij(m)为由t时刻状态Ei经过m步转移到t+1时刻状态Ej的原始数据样本数，Mi为处于状态Ei的原始数据样本数，则称

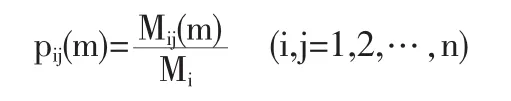
为状态转移概率，p(n)=(pij(n))为n步转移概率矩阵。在实际中，一般只要考察一步转移概率矩阵P(1)。设预测对象处于Ek状态，考察P(1)中第k行，若maxpkj=pkl，则下一时刻系统最有可能由Ek状态转向El状态。当矩阵P(1)中第k行有两个或两个以上概率相同时，状态的未来转向难确定。此时，需要考虑多步转移概率矩阵P(n)(n≥2)。

(3)确定预测值

由状态转移概率矩阵确定t+1年残差所处状态El，取El所属状态区间[El-,El+]的中位数作为第t+1年的残差，结合线性回归模型的预测值，得出事业编制总量的预测值：

2 应用实例

收集江西省1990～2008年相关数据，用SPSS16.0软件对初始指标做因子分析。其中事业编制规模的数据来源于《江西省事业编制统计》和《江西统计年鉴》（1991～2008）。

在对初始指标体系的因子分析中，KMO测度值为0.830，巴特利特球体检验的χ2统计值的显著性概率值是0.000，说明数据具有相关性，适合做因子分析。经过因子分析，得到2个公因子，它们解释了总体方差的89.82%，因此，可以用这两个公因子的值进行后续分析。正交旋转后的因子负载结果如表1所示。

从负载矩阵可以看出，因子1对第三产业就业人数、人口、电视人口覆盖率、生产总值、中等教育学生数和事业费等有较大影响，反映的是社会生活与经济发展状况，因子2对卫生技术人员和初等教育人数等影响大，反映的是教育、卫生事业人员变化情况。因子得分系数如表2所示。

根据因子值和事业编制总量数据，用EViews5.0软件，可以得到如下回归结果：

Y^t=74.02955+11.70403F1t+1.39351F2t-4.379813DtF1t

(162.4298) (18.04703) (3.257159) (-4.178786)

R2=0.983417 S.E=1.355773 DW=1.998851

该回归方程的拟合度较高，也基本不存在自相关现象，可以用来对事业编制规模做预测。回归预测结果见表3。

根据各年事业编制规模实际值与预测值的残差大小，按近似等概率将其分为四个状态：

E1:[-2.1929,-1.0023]；E2：[-0.5982,-0.1724]

E3：[0.1884,0.8808]；E4：[1.0220,1.7471]

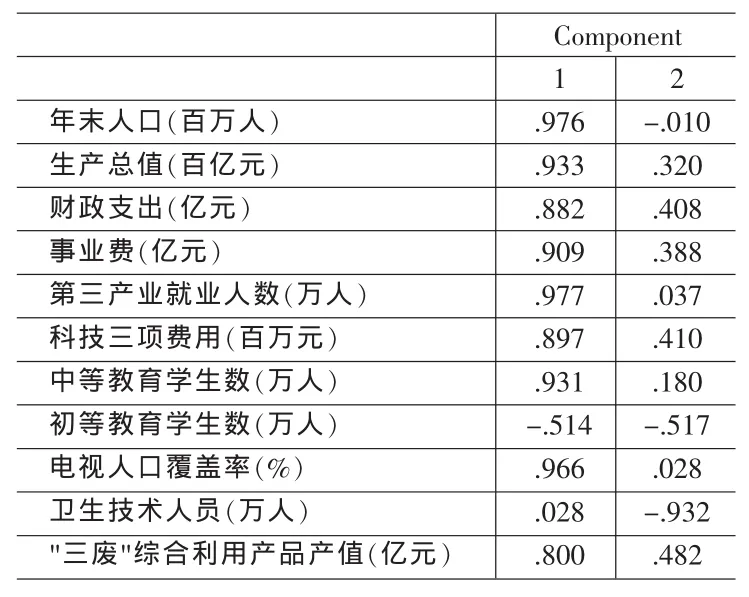
表1 旋转后的因子的负载值表

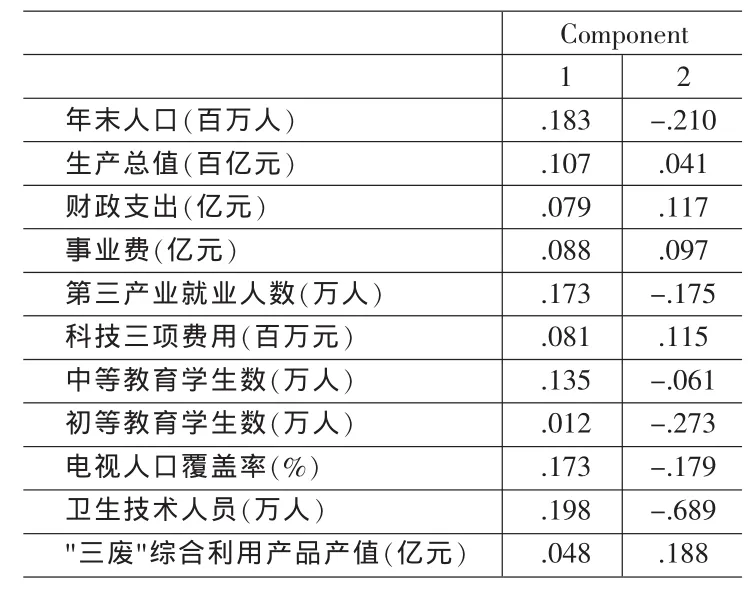
表2 计算因子值的系数矩阵

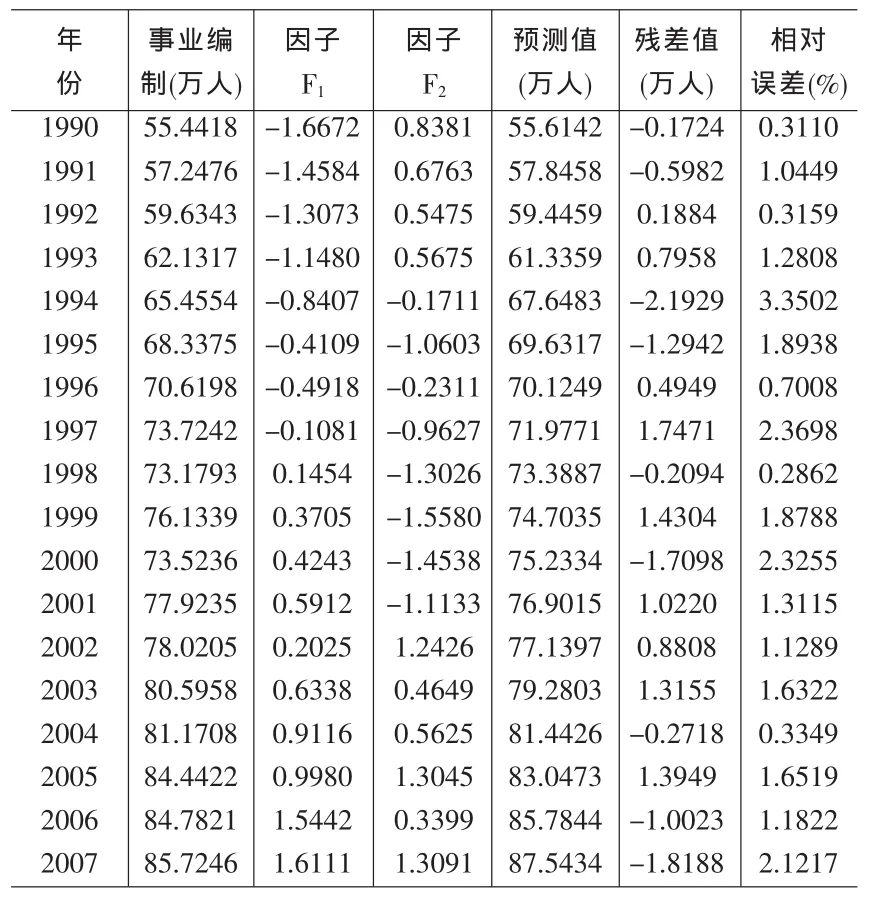
表3 回归预测结果

残差转移概率矩阵p为：

2007年残差处于E1状态，由maxp1j=p11得出2008年残差处于E1状态。取E1状态区间[-2.1929,-1.0023]的中位数作为2008年的残差。

通过曲线估计可得2008年因子 F1、F2的值分别为1.7470，0.6524.

将上述因子值和残差值代入(2)、(3)式，可得2008年事业编制总量预测值为86.0816万人。需要指出的是，回归预测一般应限于原数据所包括的范围内，当变量超出范围较小时，可以做短期近似预测。实际值为86.4973万人，相对误差为0.48%。因此，这种方法具有较高的预测精度。

3 结语

事业编制规模受区域社会经济水平、公共事业现状以及人们对公共产品和服务期望等因素的影响制约，通过因子分析对这些因素进行浓缩，建立含因子和虚拟变量的回归模型预测编制规模。考虑到事业体制处于变革时期，政策环境不仅使得编制组成在变革前后有显著差异，而且造成编制总量调控在变革的不同阶段的效果不同，实际事业编制规模呈现“精简——膨胀——再精简——再膨胀”的特点。为了更好地解释这种随机波动现象，有必要结合马尔可夫链对回归预测结果进行修正。对江西省的实例分析证明了其有效性。值得注意的是，事业编制改革是一个持续的变化过程，对编制规模的预测应该是面向短期的。

[1]杨小斌,邓群钊,彭峰等.公共事业编制规模预测研究——以江西省为例[J].南昌大学学报（人文社会科学版）,2008,39(4).

[2]马树才,胡立杰,王威.地方行政、事业机构编制配置与总量控制研究[J].统计研究,2005,(9).

[3]李彬,田皓.社会事业评价指标体系的建立及应用[J].统计与决策,2005,(8).

[4]彭国甫.地方政府公共事业管理绩效评价研究[M].长沙:湖南人民出版社,2004.

[5]唐任武,唐天伟.2002年中国省级地方政府效率测度[J].中国行政管理,2004,(6).

[6]贺福利,胡勇,陈淳.用灰色马尔柯夫链预测模型对我国粮食产量的预测[J].数学的实践与认识,2003,33(12).

[7]姚奇富,李翠凤,马华林等.灰色系统理论和马尔柯夫链相结合的网络流量预测方法[J].浙江大学学报（理学版）,2007,34(4).