基于FrFT的LFM相参脉冲信号多普勒频率变化率估计算法

李 宏 秦玉亮 李彦鹏 王宏强 黎 湘

(国防科技大学电子科学与工程学院 长沙 410073)

1 引言

运动辐射源相对于观测平台的径向加速度信息反映在观测信号的多普勒变化率中，利用多普勒频率变化率信息可以对辐射源进行无源定位和跟踪，其定位和跟踪的速度和精度优于传统基于角信息的定位方法[1]。在实际场景中，受实际目标运动速度和雷达载频的限制，反映到观测信号中的多普勒频率变化率非常微弱，通常为102Hz/s量级[2]。而在无源定位与跟踪系统中，对多普勒频率变化率的估计精度要求精确到100Hz/s量级，因此高精度提取多普勒频率变化率是实现这一类无源定位与跟踪的关键技术。目前，大多数雷达采用LFM脉冲压缩波形，如火控雷达、探测、成像雷达等，脉冲宽度通常为微秒量级，通过对单个脉冲信号的处理提取多普勒频率变化率很难满足无源定位和跟踪的要求。

近年来，许多研究者开展了利用雷达相参脉冲串信号的相参特性提高多普勒频率变化率估计精度的研究。文献[2]通过对相参脉冲在载频处的离散傅立叶变换谱做相关运算实现了多普勒频率变化率的精确估计；文献[3]利用小波变换的时频局部化特性抑制噪声，获得了多普勒频率变化率的高精度估计。但对脉内存在调制的LFM相参脉冲信号，该些方法并不适用。文献[4]通过相参脉冲间的相关运算消除脉内调制的影响，但相关运算引入了信号与噪声的交叉项，算法估计性能非最优。文献[5]通过计算脉冲信号在小波脊线上的渐进小波变换在尺度域上抑制噪声，提高低信噪比时多普勒频率变化率的估计精度。从充分利用LFM信号能量提高信噪比角度分析，小波变换不是最优的。对于LFM信号，分数阶Fourier变换与匹配滤波等效，可获得最大输出信噪比[6]。本文将分数阶Fourier变换应用于LFM相参脉冲多普勒频率变化率估计问题，提出了一种新的多普勒频率变化率高精度估计算法。

本文第2节简单介绍了分数阶Fourier变换的定义；第3节给出了观测LFM相参脉冲信号模型；第4节详细推导了基于分数阶Fourier变换的LFM相参脉冲信号多普勒频率变化率估计算法，并给出了估计方差的理论值；第 5节推导了参数估计的Cramer-Rao下界的表达式；第6节为算法性能分析及仿真实验，最后为本文的结论。

2 分数阶Fourier变换

分数阶Fourier变换是对经典Fourier变换的推广，具有时频旋转特性，是一种统一的时频变换。近年来，在光学、信号处理等领域得到越来越广泛的应用。

分数阶 Fourier变换离散快速算法是其应用的关键，目前已经提出了几种离散型分数阶 Fourier变换快速算法，计算复杂度与传统 Fourier变换相当[8]。

3 观测信号模型

在工程应用中一般将目标辐射源和观测平台的相对距离近似展开为时间的二次项，一次项表示目标相对于观测平台径向速度，二次项表示径向加速度，在接收信号中则体现为多普勒频率和多普勒频率变化率。文献[2-5]中，均假设观测平台在目标雷达一次扫描内接收到的信号时长很短，将此时间内多普勒频率变化率近似为一常量，本文沿用这一假设。

观测平台接收到的 LFM 相参脉冲信号可表示为

4 分数阶Fourier变换估计多普勒频率变化率算法

4.1 相参LFM脉冲信号的分数阶Fourier变换

观测信号模型式(6)的分数阶 Fourier变换可表示为

图1 I(x,y)的幅度和相位响应

利用式(10)进行参数估计需要进行 2维搜索，当对估计精度较高时，需要很大的运算量。文献[9]提出的拟Newton算法可兼顾精度和运算量的要求，关于迭代初值的选取可参考文献[10]。

由式(16)，式(17)可见，相参脉冲串信号中各LFM 脉冲在分数阶 Fourier变换域(α︿,uˆ)处变换不仅保留了原脉冲串相位间相对关系，即保留了相参性，而且充分提高了信噪比。

4.2 多普勒频率变化估计算法

根据文献[11]，若式(16)表示信号的信噪比较高(≥10 dB)时，高斯白噪声~εp可等效为零均值实相位高斯白噪声ξp，式(16)的相位测量值可表示为

4.3 快速处理算法

前述算法需要对脉冲串中每个脉冲进行分数阶Fourier变换估计参数fp和κd，需要很大运算量。根据式(12)-式(16)的分析可知，若获得脉冲串中一个脉冲的参数估计值，假设在分数阶Fourier变换域该估计值表为 (,)，那么只需计算所有脉冲信号在(,)处的分数阶 Fourier变换值，这一简化处理避免了对每个脉冲都进行大运算量的调频斜率和等效载频参数估计过程，可大大降低算法的运算量，但对 ()的估计精度要求稍高。

5 多普勒频率变化率估计的Cramer-Rao下界

6 性能分析与仿真实验

6.1 统计性能分析

6.2 仿真实验

为了检验本文多普勒频率变化率估计算法的性能，利用Matlab2008a对其进行了Monte-Carlo仿真实验。仿真的中频信号参数设置如下：中频频率：fI=30 MHz；脉冲重复频率：fprf=1 kHz；脉冲宽度：τ=8 μs；带宽：B=4 MHz；多普勒频率变化率真值：=62.5 Hz/s；采样频率：fs=100 MHz；观测时长：Tob=50 ms。

对算法在不同信噪比下分别进行了 500次Monte-Carlo仿真试验，信噪比从-20 dB到20 dB，步进2 dB，仿真结果如图2所示，图中还给出了文献[4,5]中算法的仿真结果作为比较项。从中可以看出，在LFM脉冲调频率和初始频率满足一定精度条件下，本文多普勒频率变化率估计算法估计性能在信噪比大于-10 dB时与理论分析吻合较好。文献[4]中基于脉冲间相关方法在高信噪比时与理论分析结果一致，但在低信噪比时，与理论结果有较大偏差，不是最优估计，这与文献[4]中分析结论一致。文献[5]中基于渐进小波变换方法的估计性能与所选取的小波脊线变换点有关，图2给出了一组较好的结果，但在高信噪比下与理论结果仍有较大偏差。

通常相参脉冲雷达的脉冲重复频率稳定度很高，短期稳定度达到 1 0-10Hz/s量级，对算法的影响非常小。

7 结论

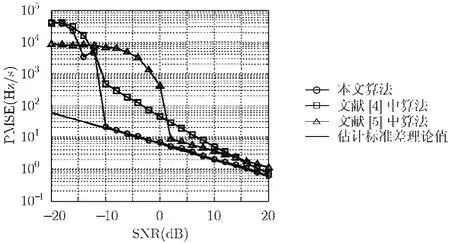
图2 不同多普勒频率变化率估计性能

本文提出了一种基于分数阶 Fourier变换的LFM 相参脉冲信号多普勒频率变化率高精度估计方法，通过对信号进行分数阶Fourier变换在分数阶变换域充分提高了信噪比，分数阶Fourier变换结果进行相关变换完成相位差分，消除相位模糊，获得了多普勒频率变化率的最小方差估计。在脉冲重复频率稳定度很高时，本文算法估计精度简接近理论下界，相比已有算法具有更低的信噪比门限，可用于低信噪比条件下 LFM 相参脉冲信号多普勒频率变化率估计。

[1] 冯道旺. 利用径向加速度信息的单站无源定位技术研究[D].[博士论文], 长沙, 国防科技学技术大学, 2003.

[2] 冯道旺, 周一宇, 李宗华. 相参脉冲序列多普勒变化率的一种快速高精度测量方法[J]. 信号处理, 2004, 20(1): 40-43.Feng Dao-wang, Zhou Yi-yu, and Li Zhong-hua. A fast and accurate estimator for Doppler rate-of-change with the coherent pulse train[J].Signal Processing, 2004, 20(1): 40-43.

[3] 郁春来, 吕韶昱, 万方等. 基于小波变换的多普勒频率变化率高精度估计方法[J]. 电子学报, 2007, 35(9): 1656-1659.Yu Chun-lai, Lü Shao-yu, and Wan Fang,et al.. An accurate estimation algorithm for doppler frequency rate-of-change based on wavelet transform[J].Acta Electronica Sinica, 2007,35(9): 1656-1659.

[4] 郁春来, 万建伟, 占荣辉. 一种 PCM 相参脉冲序列多普勒频率变化率估计算法[J]. 电子与信息学报, 2008, 30(10):2303-2306.Yu Chun-lai, Wan Jian-wei, and Zhan Rong-hui. An estimation algorithm for Doppler frequency rate-of-change with PCM coherent pulse train[J].Journal of Electronics&Information Technology, 2008, 30(10): 2303-2306.

[5] 郁春来, 万方, 占荣辉等. 一种关于 LFM 相参脉冲信号多普勒频率变化率的估计算法[J]. 信号处理, 2008, 24(4): 546-550.Yu Chun-lai, Wan Fang, and Zhan Rong-hui,et al.. An estimation algorithm for Doppler frequency rate-of-change with LFM coherent pulse signal.Signal Processing, 2008,24(4): 546-550.

[6] Wang M S, Chan A K, and Chui C K. Linear frequency-modulated signal detection using Radon-ambiguity transform[J].IEEE Transactions on Signal Processing, 1998,46(3): 571-586.

[7] 陶然, 邓兵, 王越. 分数阶 Fourier变换在信号处理领域的研究进展[J]. 中国科学E辑, 2006, 36(2): 113-136.Tao Ran, Deng Bing, and Wang Yue. Research progress of the fractional Fourier transform in signal processing[J].Science in China Series F: Information Sciences, 2006, 49(1): 1-25.

[8] 陶然, 张峰, 王越. 分数阶Fourier变换离散化的研究进展[J].中国科学E辑, 2008, 38(4): 481-503.Tao Ran, Deng Bing, and Wang Yue. Research progress on discretization of fractional Fourier transform [J].Science in China Series F:Information Sciences. 2008, 51(7): 859-880.

[9] 齐林, 陶然, 周思永等. 基于分数阶 Fourier变换的多分量LFM信号的检测和参数估计[J]. 中国科学E辑, 2003, 33(8):754-759.Qi Lin, Tao Ran, and Zhou Si-yong,et al.. Detection and parameter estimation of multicomponent LFM signal based on the fractional Fourier transform[J].Science in China Series F: Information Sciences, 2004, 47(2): 184-198.

[10] 胥嘉佳, 刘渝, 邓振淼. LFM信号参数估计的牛顿迭代方法初始值研究[J]. 电子学报, 2009, 37(3): 598-602.Xu Jia-jia, Liu Yu, and Deng Zhen-miao. The starting point problem of parameters estimation for LFM signal based on Newtons method[J].Acta Electronica Sinica, 2009,37(3):598-602.

[11] Tretter S A. Estimating the frequency of a noisy sinusoid by linear regression[J].IEEE Transactions on Information Theory, 1985, IT-31(6): 832-835.

[12] Händel P and Tichavský P. Frequency rate estimation at high SNR[J].IEEE Transactions on Signal Processing, 1997,45(8): 2101-2105.

[13] Ristic B and Boashash B. Comments on “The Cramer-Rao lower bounds for signals with constant amplitude and polynomial phase”[J].IEEE Transactions on Signal Processing, 1998, 46(6): 1708-1709.

[14] 刘建成, 刘忠, 王雪松等. 高斯白噪声背景下的 LFM 信号的分数阶 Fourier域信噪比分析[J]. 电子与信息学报, 2007,29(10): 2337-2340.Liu Jian-cheng, Liu Zhong, and Wang Xue-song,et al.. SNR analysis of LFM signal with gaussian white noise in fractional fourier transform domain[J].Journal of Electronics&Information Technology, 2007, 29(10): 2337-2340.

[15] 刘建成, 王雪松, 刘忠等. 基于分数阶Fourier变换的LFM信号参数估计精度分析[J]. 信号处理, 2008, 24(2): 197-200.Liu Jian-cheng, Wang Xue-song, and Liu Zhong,et al.Parameters resolution of LFM signal based on fractional fourier transform[J].Signal Processing, 2008, 24(2): 197-200.