多基站协作系统中有限反馈策略及其码本设计

肖尚辉 张忠培 史治平(电子科技大学通信抗干扰国家重点实验室 成都 611731)(宜宾学院物理与电子工程学院 宜宾 644007)(东南大学移动通信国家重点实验室 南京 211189)

1 引言

近年来，在多输入多输出(Multiple Input Multiple Output，MIMO)无线系统中，为了能增强信号覆盖范围，提高系统空间自由度以及宏分集效果，改善信道秩，减小小区边缘同频干扰(Co-Channel Interference，CCI)影响等，以适应新一代无线移动通信系统的需要，提出了一种多基站协作传输的网络MIMO模式，相对于传统基站非协作方式而言，多基站协作将来自邻近小区的干扰信号变成有用信号，可有效地消除 CCI，进而有望获得更大的系统容量和更高的频谱效率[1]，因此已成为协作通信领域的研究热点[2,3]。但是，该系统结构最大的特点，即是需要在现有蜂窝无线系统基础上将分布在不同地理位置的多个基站通过大容量低时延的光纤骨干网络连接到中央控制单元(Central Control Unit，CCU)，以便于基站间交换用户数据，共享信道状态信息(Channel State Information，CSI)，执行优化调度以及协作联合信号发射等[4]。为了减小系统复杂度，降低系统实现成本，目前，已提出了一种无需光纤骨干网络与 CCU单元的多基站分布式协作的网络MIMO体系结构[5]，由于该体系结构取消了用于传输和调度基站间协作信息的光纤骨干网与CCU单元，因此，可较容易地实现从现存蜂窝无线通信系统的平滑过渡。但是，要求每个用户接收端将通过信道估计得到的CSI信息反馈给参与协作通信的所有基站发射端。本文主要针对多基站分布式协作系统提出了一种基于CSI量化码字索引信息的低速率有限反馈策略，给出了实现其有限速率反馈的量化码本空间设计准则和构造算法，并分析了该机制对系统性能的影响。

2 多基站分布式协作系统

如图1所示为多基站分布式协作的网络MIMO系统结构示意图，在系统中发射天线分布在不同地理位置的多个基站，且各基站不需要通过光纤骨干网连接到一个额外增设的CCU单元，以此来控制参与协作传输的各基站以及共享CSI信息，从而可明显降低系统复杂度，减小系统实现成本。

图1 多基站分布式协作的网络MIMO系统结构

若系统中有M个分布在不同地理位置的基站，有K个移动用户，则假设参与有限协作簇的基站数为B(B≤M)，被调度参与服务的用户数为ξ(ξ≤B)。为简化分析，主要考虑各基站和移动用户均为单天线的频率平坦衰落情况，且忽略用户接收端CSI估计误差、量化误差以及反馈时延、反馈误差等的影响。若将系统中所有基站发射天线视为输入，所有用户接收天线视为输出，则可构成一个“虚拟多天线MIMO系统”。相应地，由B个基站构成协作簇同时为ξ个用户服务时，被调度用户的接收信号矢量可表示为

通过ZF预编码处理，则可有效地消除基站协作簇内的干扰。因此，如何在基站端有效获得信道矩阵H(ξ)至关重要，特别是在多基站分布式协作系统中，需要将用户端估计得到的CSI信息反馈给参与协作传输的所有基站发射端，致使额外开销的数据量非常庞大。因此，针对多基站分布式协作系统，讨论和研究低速率的有限反馈策略及其实现，具有非常重要的现实意义。

3 低速率有限反馈策略

在早期多用户信道信息反馈策略研究中，较为成熟的有模拟导频重传方法[7]，但该方法的最大不足是极易受到噪声的影响，致使系统性能恶化，吞吐量只能达到理想情况的40%。目前，在大量的单用户MIMO系统反馈机制研究中都开始着手研究一些数字的有限反馈方法。

假设用户端通过一定的信道估计能获得完美的CSI，则通过量化、编码为数字信息，并经适当的数字信号处理后，可实现将CSI有限速率反馈到参与协作簇的所有基站端，从而构成一闭环系统，如图2所示，使基站发射端能自适应地根据信道条件选择信号发射模式和发射方法，以及最优发射功率分配等[8]。

对于有限协作簇的基站数为B，被调度参与服务的用户数为ξ，且各基站和用户均为单天线的系统来说，若直接把用户端估计得到的信道矩阵元素视为一系列的复数来量化，同时独立编码每个复数，如果用Gb比特表示一个浮点数，则总的量化比特数为2GbBξ。因此，需要系统的额外开销成本较高，假如基站端和用户端均为多天线情形，则需要反馈的数据量更是非常庞大。

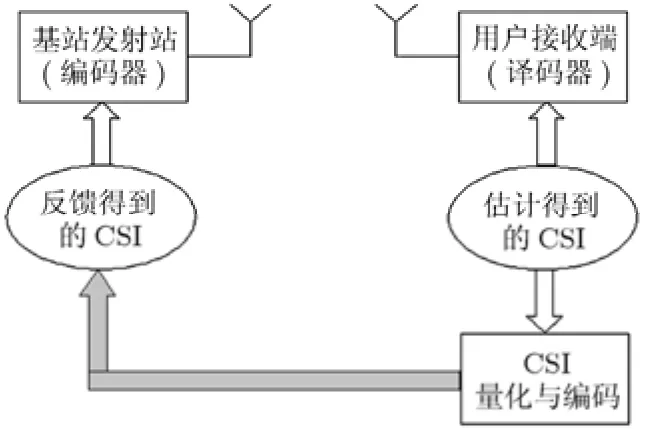
图2 信道CSI信息的有限反馈系统示意图

如果能将用户端估计得到的信道矩阵H(ξ)根据不同用户划分为一系列的复矢量，即为

如果分配Gcb比特表示量化码本空间中相应码字的索引信息，则每个子载波需要反馈的总比特数仅为Gcbξ，从而可大大降低反馈数据量，减小系统额外开销，因此，特别适合在要求低反馈比特数情况下的有限速率信道反馈实现。此外，该反馈策略还有利于处理多用户间的干扰影响，可方便推广应用到非协作情况下的多用户MIMO系统。

4 码本设计与构造

4.1 码本设计准则

信道量化的码本空间C可表示为

4.2 码本构造VQ算法

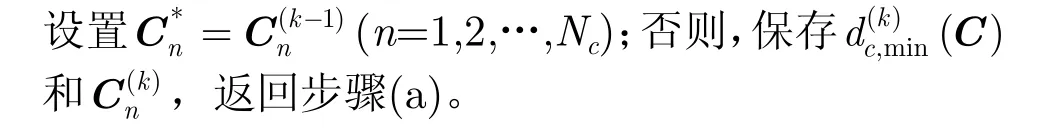
(4)重复步骤(2)，步骤(3)，直到获得期望的量化码本空间大小，迭代结束。

此外，LBG-VQ迭代算法在构造量化码本空间时，较之格拉斯曼(Grassmann)子空间压缩算法[12]而言，可获得更好的空间距离特性。比如，在2基站1用户情况下，若码字索引信息的量化比特数为3，则LBG-VQ迭代算法可获得的最小码本距离为0.3895，而格拉斯曼子空间压缩算法可获得的最小码本距离为0.3820。而在3基站1用户情况下，若码字索引信息的量化比特数仍然为3，则LBG-VQ迭代算法可获得的最小码本距离为0.5706，而格拉斯曼子空间压缩算法可获得的最小码本距离为0.5429。因此，基于LBG-VQ迭代算法的码本设计，保证了各个码字之间的最小距离最大化，即在码字数目有限的情况下，可使得所有码字在码本空间内尽量均匀地分布。

5 性能分析

在分析中，主要考虑协作基站数B=3，调度用户数ξ＝2，且均为单天线的协作簇系统，3个基站协作向2个用户传输数据。此外，小区半径为600 m；采用3GPP的空间信道模型SCM；以OFDMA作为数据传输方案，仿真中主要考虑一个子载波情形，基站发射功率为10 W，且平均分配到1024个子载波上。另外，系统采用 ZF预编码方式，以用户接收 SINR作为衡量依据，分析单个用户在不同情况下获得的累积分布函数(Cumulative Distribution Function，CDF)。

如图 3为分别在完美信道 CSI、TDD模式的CCU协作、模拟导频重传以及FDD模式的信道量化反馈等4种情况下获得的系统性能，从图中可看出，在50%中断SINR情况下，码本空间大小为8的 3 bit量化反馈策略较模拟导频重传而言可获得3.1 dB增益，而与CCU协作TDD模式相比较仅差4.7 dB。在FDD模式下，若增加信道量化比特数，则可进一步改善系统性能，如图4所示。从图中可看出，在50%中断SINR情况下，4 bit量化反馈较3 bit量化可提高增益约1.9 dB，5 bit量化反馈较3 bit量化可提高增益约3.0 dB。与此同时，也应注意到，在实际系统中，过度增加量化比特数不仅会明显增大反馈量，而且还将引起反馈信道的误码概率随之增高。

如图5所示，分别在欧几里德(Euclid)距离量化准则和弦距离量化准则两种情况下获得的系统性能对比，仿真分析中考虑量化比特数分别取4 bit，5 bit时所获得的用户SINR累积分布函数。从图中可看出，在50%中断SINR情况下，4 bit量化和5 bit量化的弦距离量化准则较欧氏距离量化准则而言可分别获得约2.7 dB与2.9 dB的增益。此外，源于弦距离的量化准则较欧氏距离量化准则而言，将更有利于捕捉信道特性。

6 结束语

从以上分析讨论可知，在弦距离准则下基于信道CSI量化码字索引信息的低速率有限反馈策略有利于大大降低多基站分布式协作系统结构的反馈数据量，减小系统额外开销，且获得的系统性能明显优于模拟导频重传方法和欧氏距离量化准则。若能充分利用信道的时间相关性，有望进一步优化 CSI反馈机制，减小反馈开销。此外，还可进一步探讨用户端CSI估计误差、量化误差以及反馈时延、反馈误差等因素对多基站分布式协作系统性能的影响，并提出相应的改进措施和实现方案。

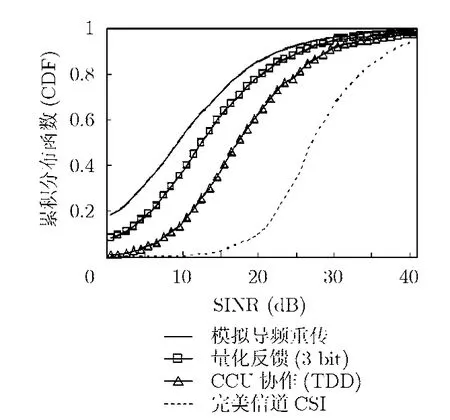
图3 在不同反馈机制下获得的用户SINR 累积分布式函数

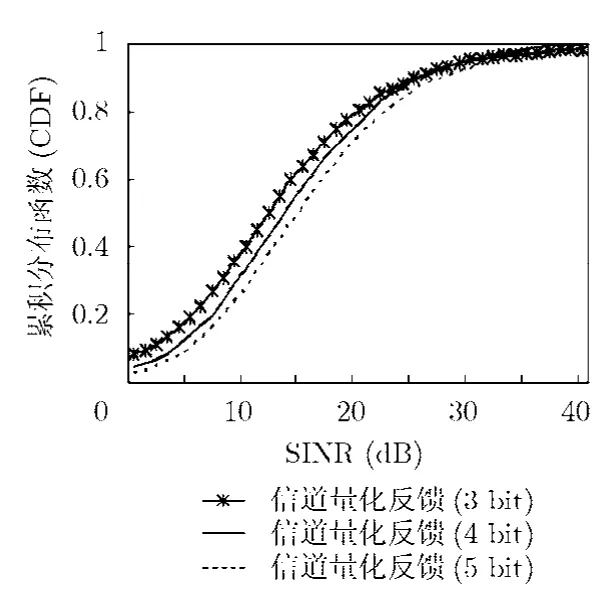
图4 在不同量化比特数下获得 的用户SINR累积分布式函数

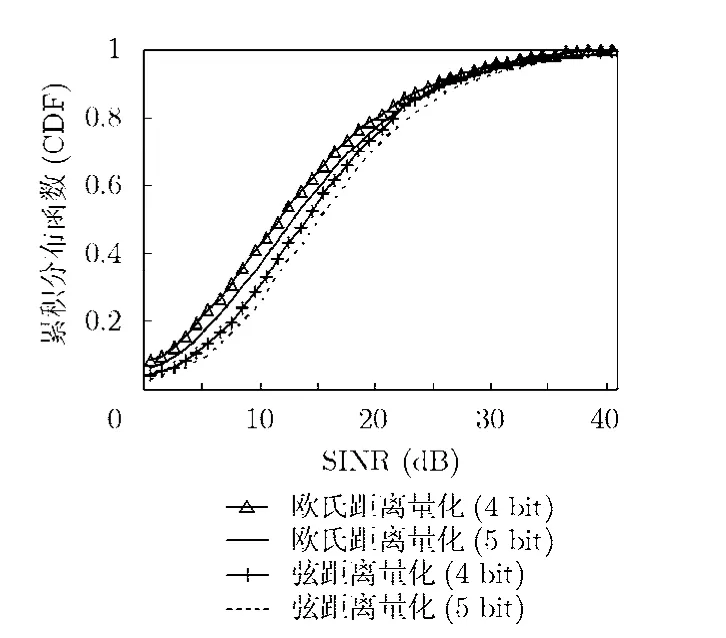
图5 在不同量化准则下获得 的用户SINR累积分布式函数

[1] Karakayali M K, Foschini G J, and Valenzuela R A. Network coordination for spectrally efficient communications in cellular systems [J].IEEE Wireless Communications, 2006,13(4): 56-61.

[2] Boon Loong Ng, Evans J S, and Hanly S V,et al.. Distributed downlink beamforming with cooperative base stations [J].IEEE Transactions on Information Theory, 2008, 54(12):5491-5499.

[3] Papadopoulos H C and Sundberg C W. Space-time codes for MIMO systems with non-collocated transmit antennas [J].IEEE Journal on Selected Areas in Communication, 2008,26(6): 927-937.

[4] Ericsson, LTE-Advanced-LTE evolution towards IMTAdvanced: Technology components [S]. TSG RAN IMT Advanced Workshop, REV-080030, Shenzhen, China, April 7-8, 2008.

[5] Papadogiannis A, Hardouin E, and Gesbert D. Decentralising multi-cell cooperative processing: a novel robust framework[J].EURASIP Journal on Wireless Communications and Networking,2009, 2009: Article ID: 890685.

[6] Yoo T and Goldsmith A. On the optimality of multiantenna broadcast scheduling using zero-forcing beamforming [J].IEEE Journal on Selected Areas in Communications, 2006,24(3): 528-541.

[7] Zirwas W, Schulz E, Kim J H, Jungnickel V, and Schubert M.Distributed organization of cooperative antenna systems [C].Proceedings of 12th European Wireless Conference, Athens,Greece, April 2006: 279-311.

[8] Love D J, Heath R W, and Lau V K N,et al.. An overview of limited feedback in wireless communication systems [J].IEEE Journal on Selected Areas in Communications, 2008, 26(8):1341-1365.

[9] Zhou S and Li B. BER criterion and codebook construction for finite-rate precoded spatial multiplexing with linear receivers [J].IEEE Transactions on Signal Processing, 2006,54(5): 1653-1665.

[10] Love D J and Heath R W. Limited feedback unitary precoding for spatial multiplexing systems [J].IEEE Transactions on Information Theory, 2005, 51(8): 2967-2976.

[11] Linde Y, Buzo A, and Gray R M. An algorithm for vector quantizer design [J].IEEE Transactions on Communications,1980, 21(8): 84-95.

[12] Love D J, Heath R W, and T Strohmer. Grassmannian beamforming for multiple-input multiple-output wireless systems [J].IEEE Transactions on Information Theory, 2003,49(10): 2735-2747.