应用于低对比度扩展目标观测的大型阵列太阳自适应光学电子系统的设计与实现

费玮玮 王长清 刘濮鲲 蔡惠智 姜爱民 唐清善(中国科学院电子学研究所 北京 100190)(中国科学院声学研究所 北京 100190)(中国科学院国家天文台 北京 100012)

1 引言

自适应光学由于可以有效补偿光的大气传输效应，达到或接近光学系统的衍射极限，被广泛地应用于天文观测中。目前已有的自适应光学系统主要是用于夜间对恒星的观测[1-4]。与这一相对成熟的夜天文自适应光学技术相比，白天对太阳观测的太阳自适应光学更具挑战性，成为自适应光学研究的难点。

针对太阳黑子或太阳表面米粒结构这一类低对比度扩展目标，通常对恒星采用的运算量较小的质心算法不再适用，一般采用协方差相关算法或者差绝对值和法[5]，这对电子系统提出了大计算量、高实时性的要求。目前基于FPGA的系统设计研究[6]，取得一定的成就，但随着系统规模的扩大，单独使用FPGA尚不能满足实际应用需求。DSP因具有强大的并行数据处理能力，被引入电子系统的设计[7]。如今，将DSP与FPGA结合起来，采用合适的优化算法，使得构建更大规模、更好实时性的自适应光学系统成为可能。

本文针对太阳表面低对比度扩展目标的波前校正的应用，设计了一种基于FFT协方差相关算法的电子系统。该系统采用阵列DSP与FPGA协同合作的架构，由低阶相关跟踪系统和高阶波前处理系统组成。系统具有较好的灵活性、通用性和扩展性。下文先对采用算法进行简单介绍，接着分析系统需求，最后给出系统的整体设计方案。该电子系统目前已初步应用于76子孔径，109单元变形镜的自适应光学验证系统，实验结果验证方案可行。

2 采用算法介绍

系统的控制带宽，是衡量自适应光学系统好坏的主要指标。在系统采样频率一定的情况下，电子系统的计算延时会直接影响到自适应光学系统的控制带宽。因此必须特别地对电子系统采用的算法进行分析和优化。

目前的相关跟踪算法中，差绝对值和法与协方差相关算法均能使用。本文选用FFT协方差相关算法。

整个电子系统算法应用过程如图1所示。先确定一个参考图像进行FFT运算后作为模板，每个实时采集的图像经过预处理后进行FFT运算，复共轭后与参考图像FFT点乘，结果再进行逆FFT变换得到相关函数值，找到匹配点后，进行5×5的抛物线拟合，所得到的相对位移与波前复原互作用矩阵进行部分积运算，得到电压控制量。

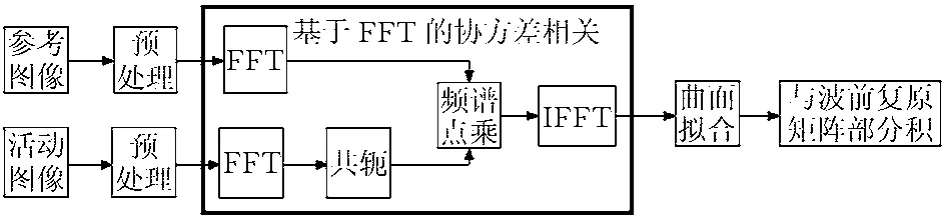
图1 相关算法框图

具体分析如下：

2.1 图像预处理

在目标为太阳米粒组织图像或太阳黑子的情况下，采用图像相关处理算法，其本质是寻找图像的最佳匹配点，从而得到图像的运动估计。对于N×N的两幅图像，根据相关的定义：

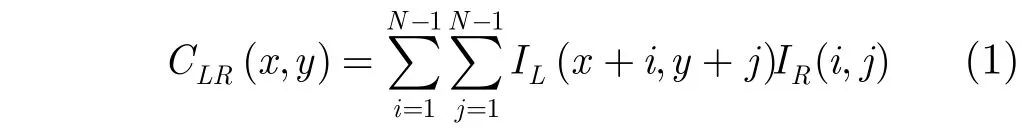
其中CLR(x,y)为相关函数，IR(x,y)是参考图像，IL(x,y)是目标活动图像。目标图像和参考图像的重叠度和相似度越大，则相关值越大，因此通过计算相关函数最大值的位置，就可以得到图像的相对移动量，也就是目标相对于参考图像的位移。

协方差相关算法来源于标准化协方差相关，就是对相关函数进行去均值和归一化处理。

2.2 基于FFT协方差相关算法

图像在预处理之后，就可以进行相关计算来求相对偏移量，但是直接计算运算量过于巨大，必须将互相关函数首先转化成FFT变换来求解。

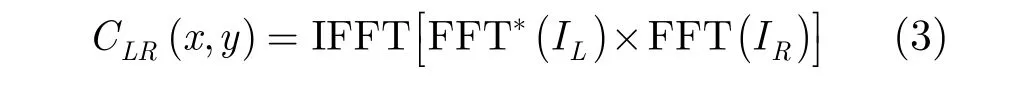
即使直接采用FFT运算量也不小，必须对算法进行进一步优化。由于图像是纯实数，可以通过变换处理使得图像序列变成一个复数序列的实部和虚部，图像的傅里叶变换是 2维的，2维离散傅里叶变换(DFT)可以利用1维基2FFT来计算优化[9]。相关算法按照步骤主要包括一次2维FFT，一次频谱点乘，一次2维逆FFT。

2.3 抛物面拟合

相关函数求得的峰值位置，只能计算出位置偏差的整像元数，为了提高计算精度，还需对相关峰进行曲面拟合，求得最接近的亚像元偏移位置。在这里取相关函数最大值(设为C(0,0))附近5×5的子矩阵作抛物面拟合，根据最小二乘法可以推得相移坐标X，Y：

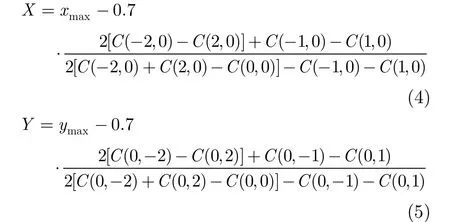
其中xmax，ymax是相关函数最大点的行列坐标。

2.4 直接斜率法[10]计算波前复原矩阵

采用直接斜率法校正波前时，首先在系统开环的情况下，对变形镜的驱动器分别施加单位控制电压，并由哈特曼波前传感器分别测量相应的波前斜率，根据控制电压V与波前斜率矩阵S间的关系式

求得斜率响应矩阵H的值，H维数为2n×m(n为变形镜校正器驱动单元的数目，m为哈特曼传感器的子孔径数)。在畸变波前进行校正闭环工作时，根据实时动态测量出的畸变波前斜率S，可根据式(7)求得所需的波前复原电压V

式中H*为H的广义逆矩阵，亦称波前复原矩阵。当2n＞m时，它们之间满足最小二乘关系，能够保证对各校正驱动单元施加的控制电压是以最小方差拟合波前探测的相位斜率。本系统中n=76，m=109。

将2.3节得到的偏移量与H*进行部分积运算，结果运用相应PID控制算法就可以求出高阶波前校正系统需要的反馈电压控制量(低阶相关跟踪系统只用偏移量即可计算控制电压)。

3 系统设计及实现

3.1 系统需求分析

参考第2节的算法，根据系统需求可以估算出系统的计算量，进行电子系统初步设计。

验证系统采用10×10的哈特曼微透镜阵列。高阶波前处理系统波前探测采用高帧频CMOS相机，窗口输出帧频最高可达2500 Hz。一共100个子孔径(又称为子窗口)，有效子孔径为76个，子孔径的划分如图2所示。根据系统需求，要求高阶系统处理能力必须达到20.52 Gflops，完成每个子孔径计算耗时＜0.04 ms。

低阶相关跟踪器探测相机采用CCD为DALSA系列，输出32 pixel×32 pixel，输出帧频＞5000 Hz，要求处理能力达到4.4 Gflops，完成全部计算在主频500 MHz的情况下，耗时＜0.18 ms。

图2 子孔径阵列排布

3.2 系统整体设计

根据算法特点和系统要求，本文设计了基于DSP与FPGA协同合作的，由低阶相关跟踪系统和高阶波前校正系统组成的自适应光学电子系统，其结构如图3所示。其中，高阶波前处理系统其工作流程为：高帧频CMOS相机采集的高速数字图像信号通过被采集进入图像采集分发板，经过图像分割处理，分割后的图像数据通过 Link口(单向速度为450 MB/s)传输给m块图像计算处理板(每块板4片DSP)进行并行计算，计算的结果再通过 Link口汇总给控制输出板，再将校正计算的结果输出给n块32路输出的D/A板，进而产生所需控制电压对变形镜进行反馈控制。低阶相关跟踪系统工作流程与高阶系统类似，但需要在一块板上完成从图像采集、计算控制到D/A输出的所有功能。高阶低阶两个子系统均需通过PCI总线，将计算结果、控制数据存储并传至控制计算机，在计算机上实时显示监控图像。低阶高阶之间设计有连线，方便两个子系统交互数据。

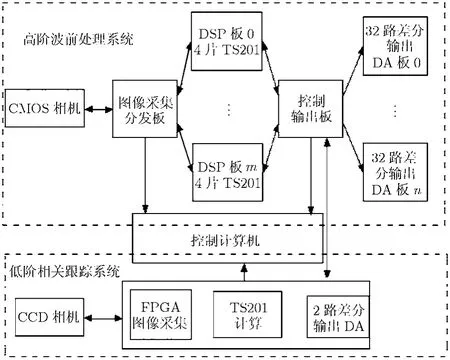
图3 天文图像信号处理实现方案

3.3 图像处理部分的设计

图像处理设计是整个系统设计的核心部分，为实现对所观测的天文图像自适应地进行高速、实时的处理，本文采用了基于DSP+FPGA的图像处理设计，包括图像采集单元、图像分割策略以及图像计算单元的设计。

3.3.1图像采集单元 在3.1节里面介绍过，电子系统通过CMOS和CCD相机来获取图像信息，高阶和低阶波前探测单元图像接口分别采用 Camera Link和RS422接口。其中Camera Link接口方式的数据传输速率高达660 MB/s，因此在设计中需要利用FPGA内部的高速、大容量Block RAM作为存储单元，对该方式的数据进行缓存，并以 Gray码对存储单元的读写地址进行编码，自行构建高速、大容量的异步FIFO。通过该FIFO的数据缓存后，系统能够实现通过多路DSP-TS201的 Link口同步传输数据给所有图像计算单元。该方式的优点是，任意的计算单元能够按时钟同步获取相同的数据，处理完毕后同步进行图像波前校正，避免出现不同的计算单元在同一时刻处理不同帧图像的情况。

3.3.2图像分割策略 在波前处理系统中，传统的策略是处理器获取一帧完整图像并储存，再通过总线寻址来获取所需数据，这对于低帧频图像比较易于实现，对本系统不再适用。对于图2所示的子孔径分布，需运用块处理的策略，将输入数据分割成块，发挥DSP并行计算的优势。在采用流水线处理的方式下，所有的DSP处于任务级同步工作，以实现高速实时处理天文图像。

为实现这一目的，本文采用基于FPGA的准实时流水线进行图像分割策略。第1步，按照上文设计，建立第1级FIFO，通过Camera Link接口取得原始图像，同时产生与数据同步的地址；第2步，由目标DSP产生图像分割参数表，具体而言就是将所选取分割区域的每个边界拐点坐标按照“包头+坐标地址”的格式写入一个参数表，由Link口发送给 FPGA，表的容量根据 Link口的要求，必须为256的倍数，实际系统中选取为1 kbyte；第3步，FPGA将每一行的数据读入第2级FIFO，再根据分割参数表得到的有效地址，将所需的数据写入第3级FIFO，通过Link口发送给对应的DSP进行处理。

3.3.3图像计算单元 针对整个系统的特点，选用ADI高性能DSP芯片TS201。该芯片具有高处理器时钟频率，合理的结构和新的存储器技术，以及高IO接口带宽，使得基于该芯片的系统性能提升，大大降低了开发成本、功耗和芯片尺寸。其主要的优点为：提供高性能静态超标量处理器，专对大的信号处理任务和通信结构进行优化；4条相互独立的128位宽的内部数据总线连接到片内 6个 4 MbitDRAM，片内带宽33.6 GB/s，运行在600 MHz时，ADSP-TS201S可以提供48亿次40位MAC运算或者12亿次80位MAC运算；14通道的DMA控制器支持优先级中断和嵌套中断；4个全双工的Link口支持单向最高500 MB/s的传输速度[11]。

图像计算单元DSP板的核心组成部分是由4片TS201、大量存储器(128MB的SDRAM)及PCI接口构成的DSP簇。图4描述了计算版上DSP簇内的Link口连接结构。

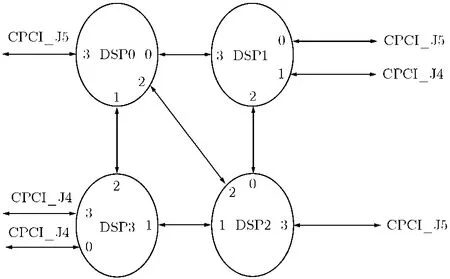
图4 TS201的Link口连接结构

特别地，针对76子孔径，109变形镜的实验系统，根据图2所示的子孔径分布，系统计算的瓶颈在中间4-7行每行10个子孔径的并行计算。可以直接使用DSP板代替控制输出板，直接采用DSP板上固定的Link口连接，起到了简化系统的作用。如图5所示，将76个子孔径分为左右两部分，分配给DSP板1和DSP板2，在4-7行需计算一行10个子孔径时，DSP板3上的DSP0和DSP2也参与计算。这样分配的结果在不影响系统传输时延的情况下，可以最大发挥DSP并行计算的优势，减少系统复杂度。根据图像分割策略，以左半边子孔径为例，每块DSP预计承担的计算任务为：DSP板1中的DSP0-4以及DSP板3中的DSP0需计算子孔径数目分别为6,10,8,10,4个。

3.4 通用性和扩展性

本系统具备强大的通用性和扩展能力，既能满足小型系统的需要，又能满足大型系统的需要。采用的DSP计算板和D/A板数目可以根据实际需求调节。系统改动时，仅需更改FPGA中的图像分割算法以及Link口的连接，硬件架构并不需要特别改动，具有较高的实用价值。

4 实验测试结果

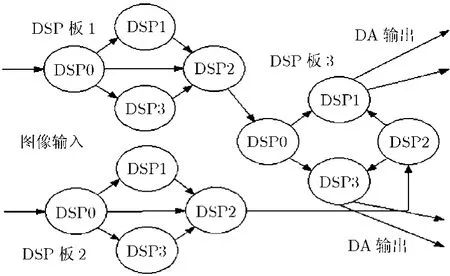
图5 实际数据流图

图6为DSP运行在500 MHz，系统调试测试时的示波器截图。图 6(a)为计算板 0上的其中两个DSP工作波形，CH1是DSP0，CH2是DSP2。第1个周期(即第1帧图像)为参考模板的计算，后面每个周期为活动图像和参考图像的相关计算。图6(b)，6(c)为参考模板的计算，在一帧图像中，每个子孔径计算时间约为24 μs(参考模板只需要计算FFT即可)，图6(d)，6(e)为活动图像与参考图像的相关计算，每个子孔径计算时间约为35 μs。从图上可以得到周期为 400 μs，反映出系统的控制带宽为 2500 Hz。

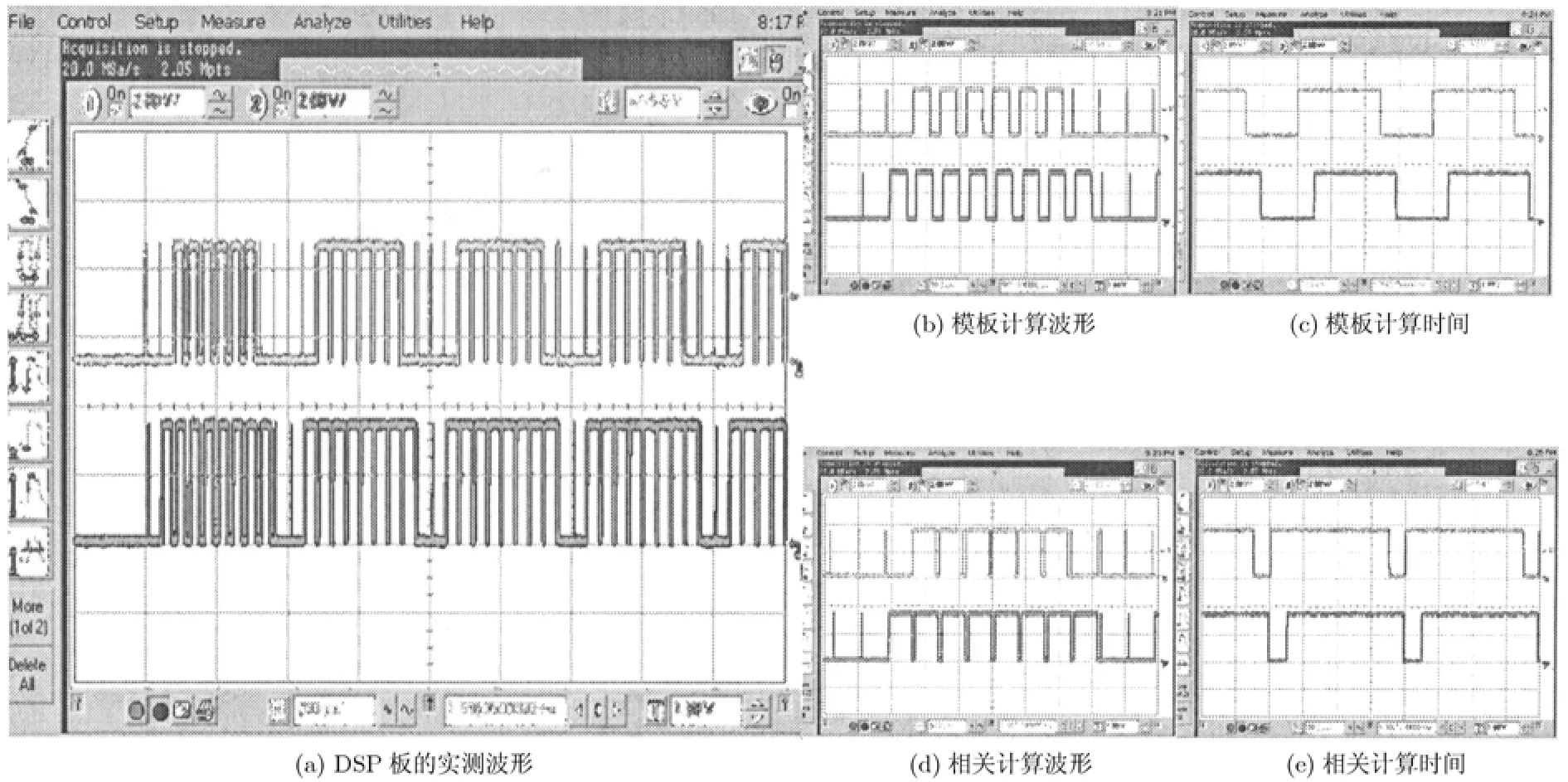
图6 示波器截图

每一帧图像由10个子孔径行组成，波形图上矩形脉冲数目的不同反应了计算分配量的不同。从图上看出，在一帧周期内，DSP0中间有 6个矩形脉冲，DSP1中间有8个矩形脉冲，这表明DSP0只有在第3-8行的子孔径参与了计算，DSP2则在第2-9行参与了计算。同理可以推断，DSP1与DSP3承担了每一行的相关运算，原因是他们几乎不参与数据在DSP板上的分配和集中，因而可以承担更多的计算任务。当图像传输处于第4-7行子孔径时，DSP板3的DSP0和DSP2也需要参加运算。这样分配的结果符合预期的设计，在采用流水线处理的方式下，所有的DSP处于任务级同步工作，系统总延时完全满足实时要求。

5 结论

本文针对低对比度扩展目标观测，设计了基于DSP与FPGA协同架构的自适应光学电子系统，选取FFT协方差相关算法，以并行流水的方式完成对相关函数的实时波前计算，达到了预先设计的目标。该系统具有较强的通用性和扩展能力，可以根据需要对计算单元和 D/A单元进行扩展，硬件实现简单，具有较高的实用价值。下一步工作是通过光、机、电系统联调，使该系统应用到太阳望远镜中。

致谢感谢戴妍峰博士，王景宇老师在论文工作期间给予的帮助。

[1] 饶长辉, 姜文汉, 张雨东等. 云南天文台1.2 m望远镜61单元自适应光学系统[J]. 量子电子学报, 2006, 23(3): 295-302.Rao Chang-hui, Jiang Wen-han, and Zhang Yu-dong,et al..61-element adaptive optical system for 1.2 m telescope of Yunnan Observatory.Chinese Journal of Quantum Electronics, 2006, 23(3): 295-302.

[2] 郑文佳, 王春鸿, 姜文汉等. 基于脉动阵列的自适应光学实时波前处理机设计[J]. 光电工程, 2008, 34(5): 44-49.Zheng Wen-jia, Wang Chun-hong, and Jiang Wen-han,et al..Design and analysis of real-time adaptive optics wavefront processor based on systolic array.Opto-Electronic Engineering, 2008, 34(5): 44-49.

[3] 闫光辉, 王春鸿, 黄奎. 基于双ADSP-TS201的波前信号处理试验平台设计[J]. 仪器仪表用户, 2008, 15(5): 89-91.Yan Guang-hui, Wang Chun-hong, and Huang Kui. The design of wavefront processing test platform based on double ADSP-TS201.Electronic Instrumentation Customer, 2008,15(5): 89-91.

[4] 高越, 赵丹培, 姜志国. 基于小波变换的空间目标图像去噪方法[J]. 电子器件, 2009, 32(3): 716-720.Gao Yue, Zhao Dan-pei, and Jiang Zhi-guo. A denoising method based on wavelet for image of space.Chinese Journalof Electron Devices, 2009, 32(3): 716-720.

[5] Rao Chang-hui, Jiang Wen-han, and Ling Nin. Tracking algorithm for low contrast extened object[J].Acta Astronmica Sinica, 2001, 42(3): 329-338.

[6] 彭晓峰, 李梅, 饶长辉. 基于绝对差分算法的相关 HS波前处理机设计[J]. 光电工程, 2008, 35(12): 18-22.Peng Xiao-feng, Li Mei, and Rao Chang-hui. Design of correlating Hartmann-Shack wavefront processor based on absolute difference algorithm.Opto-Electronic Engineering,2008, 35(12): 18-22.

[7] Rimmele T, Richards K, and Hegwer S,et al.. First results from the NSO/NJIT solar adaptive optics system[J].SPIE,2004, 5171: 179-186.

[8] Smithson R and Tarbell T D. Correlation tracking study for meter-class solar telescope on space shuttle. Lockheed Palo Alto Res.Lab.1977.

[9] 姜爱民. 相关跟踪器研制[D]. [博士论文], 中国科学院国家天文台, 2004.Jiang Ai-min. Studies on correlation tracker[D]. [Ph.D.dissertation], National Astronomical Observatories, Chinese Academy of Sciences, 2004.

[10] Jiang W H and Li H G. Hartmann-Shack wavefront sensing and wavefront control algorithm[J].SPIE, 1990, 1271: 82-93.

[11] 刘书明, 罗勇江. ADSP-TS20XS系列 DSP原理与应用设计[M]. 北京: 电子工业出版社, 2007: 6-9.