一种电磁环境复杂度快速评估方法

王伦文 孙 伟 潘高峰(通信系统信息控制技术国家级重点实验室 嘉兴 314033)(解放军电子工程学院309研究室 合肥 230037)(总参 54所 北京 100083)

1 引言

随着无线电通信设备的大量使用，电磁环境日益复杂，对复杂电磁环境问题的研究成为热点。电磁环境复杂度[1]是指在有限的时空里，一定的频段上多种电磁信号密集、交叠的程度，目前有限的频谱资源与无限增长的无线通信存在着尖锐的矛盾，对电磁环境复杂度的研究价值凸现。快速评估复杂度在民用上有利加强对频谱资源实时监督和动态管理，在军事上能够快速估计战场电磁态势，判断电磁威胁等级。

常见的电磁环境复杂度检测方法是统计某区域、某频段和某时段内，时域、空域、频域、能量域和调制域等方面的特征，通过一定模型估计复杂度[2]。文献[1]和文献[2]对战场电磁环境进行分类，选取频谱占用度、时间占用度、空间覆盖率和平均功率密度谱作为复杂度评估指标，并以此划定电磁环境复杂度等级。这种方法评估一般场合电磁环境复杂度尚可，但评估战场等重要区域则不妥，因为，它只根据统计值来评估，忽视了少数重要信号的影响。如果采用这种方法评估，那么大城市的电磁环境可能比战场的还要复杂得多。

文献[3]基于作战效能采用模糊综合评价方法估计电磁环境复杂度，文献[4]将层次分析法运用于电磁环境复杂度的评估，它们对文献[2]进行了改善，把调制域参数作为评估指标，但不能快速计算电磁环境复杂度，由于调制域参数必须对个体信号调制样式分析才能得到，而个体信号数量大，所以，这种方法速度慢。

所有信号对电磁环境复杂度都有影响，不同信号对复杂度贡献不一样，重要区域少数异常活动的信号对复杂度影响很大，而时域、空域、频域、能量域的统计特征可能对复杂度影响不一定大。因此，本文基于搜索接收机截获数据(简称搜索数据)选择可以快速获得的评估指数，剔除调制域参数为评估指数，增加异动信号率为一个重要评估指标，采用自适应神经模糊推理系统(ANFIS)对电磁环境复杂度评估。

论文第2节讨论了电磁环境复杂度评估的参数选择和异动信号发现[5]方法，第3节研究评估模型，第4节给出一个评估实例，验证算法。

2 评估参数与异动信号发现方法

影响电磁环境复杂度的参数较多，人们主要从时域、空域、频域、能量域和调制域考虑，为了快速获取电磁环境复杂度，必须及时获得评估参数，目前时域、空域、频域、能量域参数通过搜索数据可以实时提取，但是，调制域参数必须对所有信号进行调制样式分析才能得到，所以不可能实时获得。虽然信号的调制样式一定程度上反映了电磁环境的复杂程度，但无法快速得到，不能作为指标。

以上方法对复杂度评估主要从统计特征出发，没有考虑个体电台的影响，实际上电磁环境是所有个体辐射源贡献的总和。在估计电磁环境时，个体信号发挥重要的作用，比如：估计战场电磁环境时，往往把敌方威胁信号和可疑信号数量作为重要的因素；在估计机场等重要场所电磁环境时，把一些违规信号、异常信号作为评估指标。一些变化异常的信号往往具备较高的威胁等级，或是违规电台信号，或是敌方通信信号，集中地反映了电磁环境激烈冲突的程度。在估计电磁环境时只考虑统计特征是不够的，正因如此，把异常信号率作为电磁环境评估重要指标。参考文献[1]构建评估指标集为：U=，其中，u1为异动信号率；u2为大信号率；u3为时间占有度；u4为空间覆盖率；u5为信道占用度；u6为平均功率谱密度；u7为背景噪声强度。其中u2至u7在文献[1]有过详细的描述。

u1是异动信号率AS，是指有异动信号的信道数ASn同评估带宽内信道数Fn的比值。

异动信号是指某信号在时间、能量和频率上发生异常变化的信号，它反映了被观察区域内电台异常活动情况，异动信号率的大小很大程度上反映了电磁环境冲突的激烈程度。异动信号可以从搜索数据中挖掘获得，异动信号率可以快速获取。但是，无线电通信信号由于受到噪声、多径效应等因素影响，异动信号率不容易提取。特别是在复杂环境下，直接从搜索数据中提取很困难，必须对数据进行预处理，文献[5]采用构造型神经网络和商空间理论进行不同粒度聚类，具体情况不再详述，这里研究基于时幅关联比较法的异动信号检测问题。

时幅关联比较法的基本思路是在采用基于构造型神经网络对前期n0(一般取 2,3)周期的训练样本进行聚类分析的基础上，统计提取常规通信电台活动的时间和幅度规律，并将其作为模本。测试时，把测试样本的同模本进行比较，检测是否异动信号。这种方法主要借助于常规通信电台在活动时间和信号幅度上相对稳定的特性。下面通过图形分两种情况讨论。

首先介绍时幅关联比较法在单周期异动信号实时检测中的思路。测试数据与同信道前一周期模本值比较，若差值超过门限判为异常信号，否则还是常规信号。如图1所示，在2维直角坐标系中，我们以某一频率的测试样本在某一时刻的信号幅度作为P点的x坐标，把对应模本在同一时刻的幅度作为P点的y坐标，则如果两信号相等，即x=y，那么P点位于y=x直线上；考虑允许误差等因素，我们设定距离直线y=x位于d的两条直线l1,l2内部，则认为测试样本正常，否则即为异常。

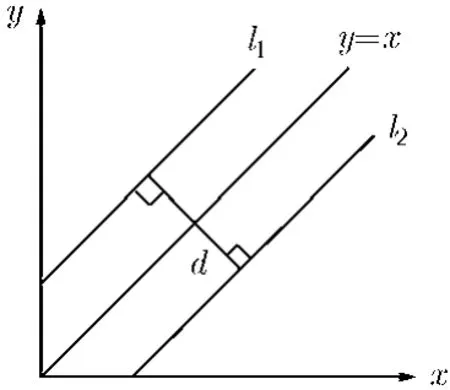
图1 允许误差范围

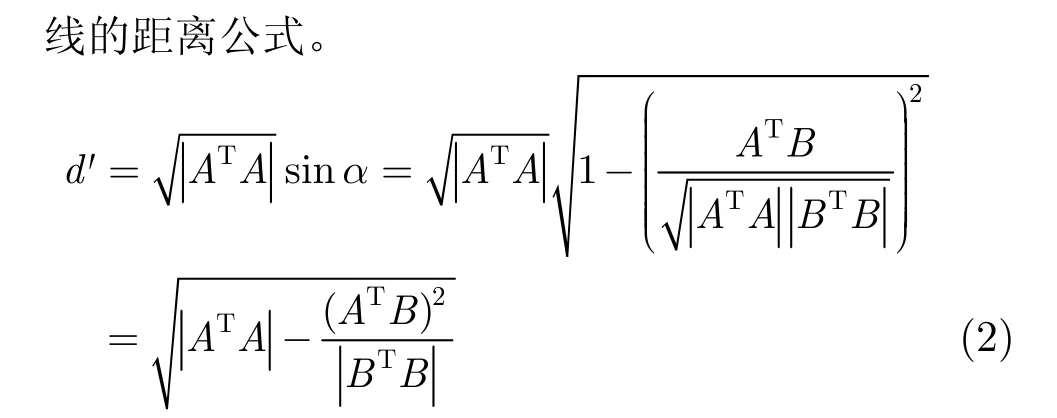
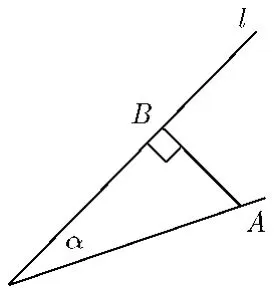
图2 点到直线距离

本例中设定阈值d，当d′＜d判断信号活动正常，当d′＞d判断它为异常。

总之，以上通过训练样本学习得到信号活动规律的模本，将训练样本与测试样本映射到2维或多维空间，计算他们之间的欧氏距离，根据距离大小发现异动信号。

图3是2009年3月22日至24日频率为15726 kHz信号的时幅图，图3 (a)为原始时频图，图3 (b)为经预处理时幅图。以前两天数据为训练样本，能得到信号活动规律的模本，以第3三天数据为测试样本，采用时幅关联比较法，能判断该信号为异动信号，椭圆内频谱为异动点。

图4为2009年3月22日至24日，15至16 MHz频段内频率占用度图，其中横轴代表时间，以天为单位，纵轴代表频率，以MHz为单位，图中点的实虚代表该点对应的时间和频率上信号的有无。从该图中直接发现异动信号比较困难，采用构造型神经网络聚类后，得到图5所示频率占用度图，以前两天数据为训练样本，经处理可以得到图6所示的模本，以第3三天数据为测试样本，可以得到图7所示的异动信号，经统计可以得到异动信号率。

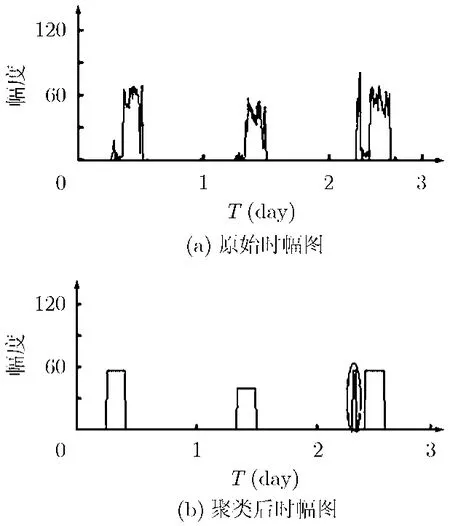
图3 15726 kHz信号3天时幅图

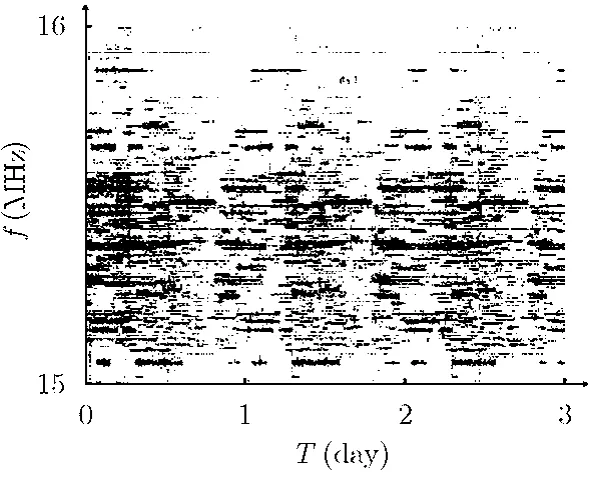
图4 15～16 MHz原始频率占用度图

图5 15～16 MHz预处理后频率占用度图

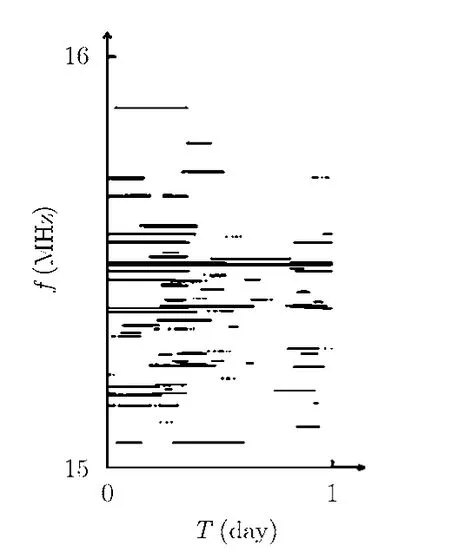
图6 模本的频率占用度图

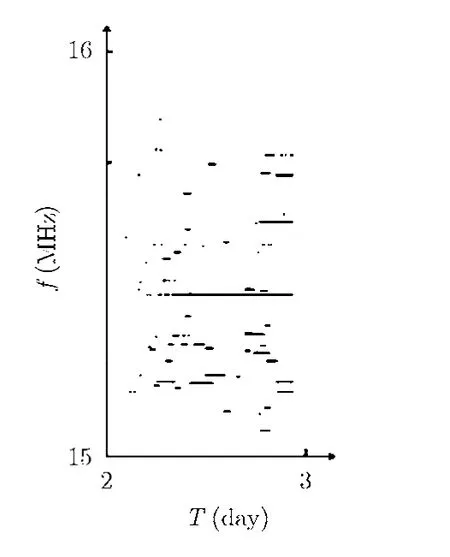
图7 异动信号频率占用度图

3 基于ANFIS的复杂度评估

模糊推理系统的结构非常适合表示人的定性或模糊的经验和知识，但本身不具备自学习功能，对专家经验的过分依赖。神经网络能够自学习，具有自适应能力。两者结合，构成神经模糊系统，既具备人工神经网络自适应学习的功能，又具备模糊控制描述和处理模糊信息、进行判断和决策的功能[6,7]。

ANFIS的网络结构[8]如图 8，是一个改进的前馈直觉模糊神经网络，可分为5层，每层物理意义明确，且模型计算简单，精度高，收敛速度快。其中节点间的连线表示信号流向，方形节点表示带有可调参数的节点，圆形节点表示不带有可调参数的节点。假定ANFIS有两个输入x和y，单输出为f，对于1阶Sugeno模糊推理系统，对应的规则形式如下

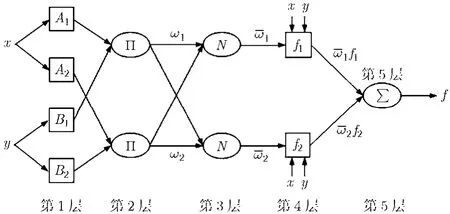
图8 自适应神经直觉模糊推理系统结构图

从ANFIS网络模型的输入输出可看出，网络的学习是对前提参数和结论参数的调整。ANFIS的建模主要结构辨识和参数辨识。ANFIS结构辨识最核心的内容是输入空间的划分，文中采用基于减法聚类的ANFIS评估电磁环境的复杂度。

4 实验分析与结论

实验分成数据截获、模型建立和测试评估3个阶段。数据截获时，在某地域选择9个有代表性的地点，假定该地域为正方形地域，可选择九宫格中每个方格的中心为采集地点。每个地点设置一台短波搜索接收机，使其在15 MHz至16 MHz频段内截获搜索数据，作为实验数据，图4是其中一台短波搜索接收机截获数据的频率占用度图。

模型构建时，将前面一半数据作为训练数据，后面一半作为测试数据。首先，对训练样本进行减法聚类，可以确定模糊规则和隶属度函数的个数，并生成ANFIS的初始模型。本实验先取聚类中心在各数据维上的影响范围，得到输入、输出向量的 4个聚类中心，即ANFIS的4条初始模糊规则。然后，将训练样本输入初始ANFIS模型，通过学习，能够有效地计算出隶属度函数的最佳参数，使得最终的ANFIS模型能够最好地模拟出希望的或是实际的输入输出关系。根据模型输出值的大小可将电磁环境分为一般、轻度复杂、中度复杂和重度复杂电磁环境4个等级。训练得到ANFIS网络如图9所示。

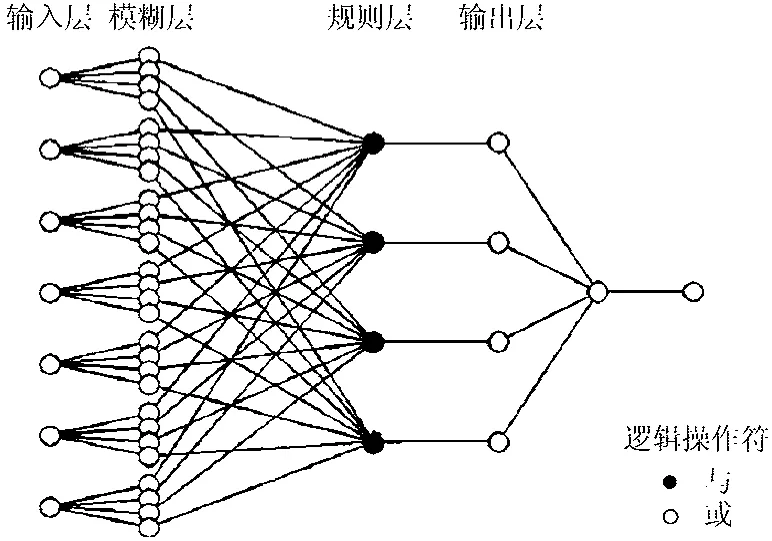
图9 ANIFIS模型结构图

测试评估时，将各短波接收机截获的实验数据按照频率划分为3个测试评估频段，分别为15.00～15.30 MHz，15.30～15.60 MHz，15.60～15.90 MHz。以每个频段测试数据为评估对象，验证评估模型的有效性。在测试前要计算异动信号率等7个输入指标集。如表1所示，将3个评估对象的7个指标分别作为ANFIS模型的输入，模型的输出即为评估对象的复杂度。其中，功率密度和背景信号强度为规范化的功率值，取最大值为100。

表1没把调制样式作为评估指标，任何一个评估波段内都包含几十个信号，提取每个信号的调制样式时间开销太大。如果考虑调制样式，势必降低评估速度。

根据文献[1]和表1复杂度值可知：波段1为轻度复杂电磁环境，波段2为中度复杂电磁环境，波段3为一般电磁环境。这与专家评估结果一致。从表1还可以看出：异动信号率对电磁环境复杂度影响比较大，这表明异动信号率作为评估指标是合理的。

电磁环境复杂度评估是当前研究热点，但是只有快速、科学评估才能发挥最大效益。本文系统研究了复杂度快速评估方法，根据复杂电磁环境需求和研究现状，构造了快速评估复杂度的指标集，剔除调制域参数指标，提出将异动信号率作为一个重要的指标，科学地评估复杂度；提出了基于搜索数据的异动信号发现方法，对预处理后的搜索数据进行挖掘，检测了异动信号；采用了基于ANFIS的复杂电磁环境评估方法，该方法采用减法聚类确定自适应模糊神经网络的结构，采用混合学习算法对参数进行训练，克服了收敛速度慢、训练时间长和局部极小值等问题；设计复杂度评估方案，采集实际数据实现了电磁环境复杂度动态评估，实验结果表明以上方法是有效的。该方法适合对战场、机场和重大活动区域的电磁环境复杂度评估，能为无线电监督和管理提供依据。

表1 电磁环境复杂度评估指标与结果数据表

[1] 尹成友. 国军标GJB 6520-2008, 战场电磁环境分类与分级方法[S]. 北京, 2008, 6.Yin Cheng-you. GJB 6520-2008, Classification and gradation methods for battlefield electromagnetic environment [S].Beijng, 2008, 6.

[2] 尹成友. 战场电磁环境分类与复杂性评估研究[J]. 信息对抗学术, 2007, 25(4): 4-6.Yin Cheng-you. Classification of battlefield electromagnetic environment and complexity evaluation [J].Journal of Information Countermeasure, 2007, 25(4): 4-6.

[3] 张笑韩, 余静. 基于作战效能影响的电磁环境复杂度评价方法[J]. 信息对抗学术, 2008, 26(2): 58-60.Zhang Xiao-han and Yu Jing. Electromagnetic environment complexity evaluation based on operational effectiveness [J].Journal of Information Countermeasure, 2008, 26(2): 58-60.

[4] 董志勇, 栗强. 基于层次分析法的人为电磁环境复杂程度评估[J]. 指挥控制与仿真, 2008, 30(5): 106-109.Dong Zhi-yong and Li Qiang. The research of artificial electromagnetic environment complexity evaluation based on hierarchy analysis method [J].Journal of Command Control and Simulation, 2008, 30(5): 106-109.

[5] Wang Lun-wen, Tan Ying, and Zhang Ling. A data mining method based on constructive neural networks [J].Journal of Electronics(China), 2007, 24(1): 133-137.

[6] 王坚强. 模糊多准则决策方法研究综述[J]. 控制与决策, 2008,23(6): 601-606.Wang Jian-qiang. Overview on fuzzy multi-criteria decisionmaking approach [J].Control and Decision, 2008, 23(6):601-606.

[7] 张进, 陈东锋. 直觉模糊综合评判在目标识别中的应用[J]. 吉林大学学报, 2009, 27(4): 407-410.Zhang Jin and Chen Dong-feng. Target recognition based on intuitionistic fuzzy comprehensive evaluation [J].Journal of Jilin University, 2009, 27(4): 407-410.

[8] 夏博龄, 贺正洪, 雷英杰. 直觉模糊近似推理中的可信度传播[J].计算机工程与应用. 2009, 45(15): 160-162.Xia Bo-ling, He Zheng-hong, and Lei Ying-jie. Confidence factors spreading in intuitionistic fuzzy approximate reasoning [J].Computer Engineering and Applications, 2009,45(15) : 160-162.