含时滞的房地产风险投资模型稳定性分析

姚洪兴，王娜娜

（江苏大学 理学院，江苏 镇江 212013）

0 引言

房地产是一高风险、高投入、高回报的行业，房地产投资在给投资者带来收益的同时，也可能给投资者带来风险并遭受损失。由于房地产商品受自然因素以及社会、经济、行政、心理等其他因素的影响，投资面临较多的不确定性。投资房地产时，由于房地产开发建设周期较长，所需投资额大，开发成本受土地费用、税费等不确定因素影响较大，所以具有一定的风险性。房地产开发需要较长的开发周期，加之土地资源有限，房地产供给呈现出低弹性，而市场对房地产的需求及需求变化却非常大，房地产需求呈高弹性，供给的低弹性和需求的高弹性注定了房地产只能预先生产，导致房地产的供给滞后。而房地产开发在某阶段的投资开发量和许多因素有关，例如市场上原有的房产数量，需求量，其他投资商本期的投资开发量，房产的售价以及前期市场上房产的价格都有一定的关系。

许多文献对房地产的投资风险进行了相应的研究,阮萍[1],张建旭[2]等从理论上进行了房地产投资风险研究；Osama Ahmed Jannadi[3]等从统计学角度对房地产投资风险进行描述,并构造了一个风险评价模型,用计算机对一项具体实例进行分析并针对相应的风险特征提出改进措施；Choi Hyun-ho[4]运用模糊理论并借助一款风险分析软件从参数估计和主观判断方面对建筑工程的风险进行识别鉴定、分析、评价和管理。然而由于房地产有一定的建设周期,即具有时滞效应，上一期的某些因素也会影响到本期的投资。文献[5]中谈到t-τ时物资价格和后期t时刻的物资供应量变化率满足一定的关系。

本文考虑到房地产投资开发量与本期及上期房产价格的关系，拟把时滞因素引入房地产投资开发中,建立一类含时滞的房地产风险投资模型，将时滞神经网络模型应用到房地产投资中，研究该模型平衡点存在的唯一性以得到平衡点全局指数稳定的充分条件。

1 模型的建立

假设市场上有n个房地产投资开发商，xi(t)为第i个开发商在t时刻投资开发的数量；xi(t-τ)为第i个开发商在t-τ时刻投资开发的数量（i=1，2，3，…，n）；f代表价格函数，那么 f是x的函数，f当然也是t的函数；τ为房子的建设周期即时滞；fi(x(t))，fi(x(t-τ))分别为第 i个投资商在 t和 t-τ时刻所建设房子的价格。由于t时刻的投资开发量对t-τ时刻房产价格的反映是滞后的，因此我们用下面的时滞神经网络模型来描述房地产的投资开发量：

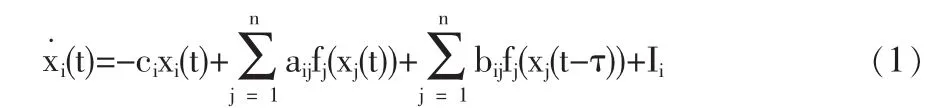
其中 n 代表开发商的数量，xi(t)、xi(t-τ)分别代表 t、t-τ时刻市场上房地产开发的数量，fj(xj(t))、fj(xj(t-τ))分别代表 t、t-τ时刻市场上房子的售价，aij、bij分别代表 t、t-τ时刻第 j个开发商房产售价对第i个投资商开发商的影响因子，0＜aij＜1，0＜bij＜1。房地产投资开发量的变化率可以用开发数量和房子价格来表示，因此，模型（1）可以表示房地产投资开发量的变化率。这里假设

C=dig(c1，c2，c3，…，cn)，A=(aij)n×n，B=(bij)n×n

2 预备知识

定义 1 称函数 x(t)=(x1(t)，x2(t)，…，xn(t))为方程（1）满足初值条件 x(s)=φ(s)，φ=C([-τ,0]，Rn)的解，如果 x(t)连续，当 t≥0 时，满足方程（1）。 特别地，称点 x*∈Rn为方程（1）的平衡点，如果 x(t)=x*是（1）的解。

定义2 一个实矩阵A(aij)n×n称为一个M矩阵，若下列条件满足：

（1）aii＞0；aij＜0；i≠j；i，j=1，2，3，…，n

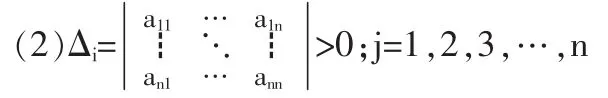
下列条件与定义2等价

（3）aii＞0；aij≤0；i≠j；i，j=1，2，3，…，n

A-1≥0，即A-1是一个非负矩阵。

定义3 假设f满足利普希兹条件，即存在一个Lipschitz常数 Li＞0 使得

|fi(x)-fi(y)|≤Li|x-y|成立。

定义 4 设 V:R+×Rn→R+，V∈V0，如果

（2）V满足局部利普希兹条件。

定义5 假设V∈V0，定义沿方程（1）的解的右导数为：

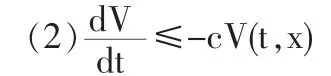
c为一常数且c＞0，则（1）的零解全局指数稳定。

引理[6]若存在 V（t，x），满足

（1）||x||≤V(t，x)≤k(α)||x||，x∈Sα={x:||x||≤α}

3 模型稳定性分析

定理1 假设f满足利普希兹条件，并且存在一正数λ和向量 z=(z1，z2，z3，…zn)T＞0，使(λE-A+(A+B)Leλτ)z＜0，则（1）的平衡点是唯一存在的。

证明：系统（1）的平衡点满足方程-(x+Af(x)+Bf(x)+I)=0定义算子T(x)=C-1((A+B)f(x)+I)

因为(C-|A+B|L)z≥(C-λE-|A+B|Leλτ)z＞0

所以必有一足够大的数r使得

(|A+B||f(0)+|I|)≤(C-|A+B|L)rz

从而C-1(|A+B||f(0)+|I||)≤(E-C-1|A+B|L)rz

即 C-1(|A+B|Lrz+|A+B||f(0)|+|I|)≤rz

设 Ω={x∈Rn，|x|≤rz}

∀x∈Ω有

|T(x)|∈C-1||A+B||f(x)|+|I||≤C-1||A+B|L|x|+|A+B||f(0)|+|I||≤rz

因此算子是有界闭集上的自映射。利用不动点定理，至少有一个不动点，它是（1）的平衡点x*。下面证明此平衡点是唯一的。

若 y*也是（1）的平衡点，则

-C(x*-y*)+(A+B)[f(x*)-f(y*)]=0

即C|x*-y*|=|C(x*-y*)|=|(A+B)||f(x*)-f(y*)|≤|(A+B)|L|x*-y*|

亦即(C-|A+B|L)|x*-y*|≤0

从(C-|A+B|L)z＞0 知 C-|A-B|L∈M

所以(C-|A+B|L)-1≥0，从而|x*-y*|=0，即 x*=y*

所以（1）的平衡点存在且唯一。

定理2 假设f满足利普希兹条件，并且有

那么系统（1）的平衡点是全局指数稳定的。

显然 V 正定，所以存在 φ1，φ2∈K，使得 φ1(||x||)≤V≤φ2(||x||)。

V沿系统（2）的Dini导数为：

当 t-τ≤s≤t，V∈V0时，有 V（s,x(s)）＜V(t,x(t))

所以 D+V(t，y(t))≤-(k1-k2)V(t,x(t))

存在 α＞0使得 k1-k2≥α

即 D+V(t,y(t))≤-αV(t,y(t))

所以系统（3）的零点即系统（2）的平衡点是全局指数稳定的。

这里的稳定是指从状态空间的任意有限非0初始状态x0出发的受扰运动x(t)=x(t，t0，x0)是有界的,且运动轨迹最终收敛于系统的某个平衡点x*,且该平衡点存在唯一性。系统(1)实质上是用一个带时滞的神经网络模型反映房地产投资开发量的变化情况。定理2说明第i个投资开发商开发数量的变化率与市场上其他投资开发商无论在本期还是上期房产的售价有关,当满足(3)式时,系统(1)是全局指数稳定的,也就是说,此时,市场上房地产投资开发量趋于稳定，与市场需求相一致，投资的风险小,可以进行投资开发。相反，如果（3）式不满足，那么市场上房地产开发量与市场需求不一致，进行投资时风险相对较大，可能给投资者造成损失。

4 结语

房地产投资本身是一项风险投资，加之投资开发周期较长，供给具有一定的滞后性，所以在房地产投资开发时把时滞因素考虑进去才更加符合实际情况。本文将时滞神经网络模型引入房地产风险投资中，基于本期开发量与上期开发量、价格的关系，建立了一类含时滞的房地产风险投资模型，分析了模型平衡点存在的唯一性和全局指数稳定的充分条件。当条件满足时，房地产投资风险较小，条件不满足时，风险相对较大。这为房地产投资开发提供了一些依据。然而，当房地产投资开发出现混沌现象时，如何通过制定切实可行的宏观调控政策以消除系统混沌是一个有待于进一步研究的热点问题。这方面研究的深入展开必将对房地产业的健康、稳定发展产生积极、深远的影响。

[1]阮萍,陈志敏.对房地产与投资风险的认识[J].经济问题探索,2000,(4).

[2]张建旭．房地产投资风险分析与防范研究[J].经营与管理,2008，(1).

[3]Osama Ahmed Jannadi,Salman Almiskari.Risk Assessment in Construction[J].Journal of Construction Engineering and Management,2003,(5).

[4]ChoiHyun-ho,ChoHyo-narn,Seo JW.Risk Assessment Methodogy for Underground ConstructionProjects[J].Journal of Construction Engineering and Management,2004,(2).

[5]丁彦栋.关于物资供应的时滞模型[J].管理技术,1994,(3).

[6]马知恩,周义仓.常微分方程定性与稳定性方法科学出版社[M].北京：科学出版社，2003.

[7]秦超.时滞动态市场模型之探讨[J].财资研究,1995,(4).

[8]曲闻.影响我国房地产价格的宏观经济因素实证分析[J].经济分析,2006,(9).

[9]朱洪亮.具有时滞的经济增长模型的控制[J].工程数学学报,2004,21(3).

[10]赵维锐,顾恩国,赵美华.具有时滞的非线性广告投资模型的全局稳定性[J].复旦学报(自然科学版),2004,43(1).

[11]彭定,江何立.基于EVA的房地产投资风险稳定性分析[J].武汉理工大学学报，2008,30(2).

[12]杨志春,徐道义．具有变时滞和脉冲效应的Hopfield神经网络的全局指数稳定性[J]．应用数学和力学，2006,27(11).

[13]廖晓昕.稳定性的理论、方法和应用[M].武汉华中理工大学出版社,1994.

[14]Teh-Lu Liao,Jun-Juh Yan,Chao-Jung Cheng,Chi-Chuan Hwang.Globally Exponential Stability Condition of a Class of Neural Networks with Time-Varying Delays[J].Physics Letters A，2005,34(3).