软性填充物对椭圆形孔洞周区应力场影响的二维分析

杨林虎，朱 涵，刘春生

(1. 天津大学建筑工程学院，天津 300072；2. 美国亚利桑那州立大学土木与环境工程学院，Tempe，AZ，85281；3. 天津市土木工程结构及新材料重点实验室，天津 300072)

含孔洞的无限大板在面内荷载作用下，在孔洞周围会产生应力集中．应力集中是一种十分普遍的力学现象，它是指受力物体应力局部增大的现象，一般出现在物体形状急剧变化的地方，如缺口、孔洞、沟槽以及有刚性约束处．应力集中一直是工程技术人员十分关心的问题．关于含圆形孔的弹性板在面内载荷作用下的应力集中问题的研究成果比较多[1-4]．关于椭圆孔引起的应力集中问题，Guo等[5]研究了横向同性的压电材料椭圆孔孔边应力集中问题；Dumir[6]分析了在面内荷载作用下矩形板的尺寸对椭圆孔孔边集中应力的影响；Hanus等[7]研究了应力集中系数与椭圆孔距自由边界距离之间的关系，并建立了统计模型. Hebel等[8]认为采用数值计算的方法研究应力集中问题时，对模型的要求很高．物体内部缺陷处有时并不是完全空的，往往会含有软性填充物，如塑料、橡胶等．然而很少见到相关文献报道填充物对孔洞集中应力和周区应力场的影响．笔者采用数值计算的方法，研究了含椭圆孔洞的矩形板在单轴拉伸作用下，椭圆形状的变化对周区应力场的影响，并采用软性填充物(弹性模量为周围介质弹性模量的 0.001倍)对椭圆形孔洞进行填充，初步探讨软性填充物对椭圆形孔洞应力集中系数、周区应力分布的影响．

1 模型的建立

含椭圆形孔洞的应力集中问题示意如图 1所示．图中椭圆表示在无限大板内的椭圆孔．a为垂直于拉力方向的椭圆的半轴长度；b为平行于拉力方向的半轴长度．在均布荷载 q 作用下，最大拉应力σmax出现在点A处．σmax随椭圆的长短轴之比λ的变化而变化．这里λ=a/ b，应力集中系数k=σmax/q．

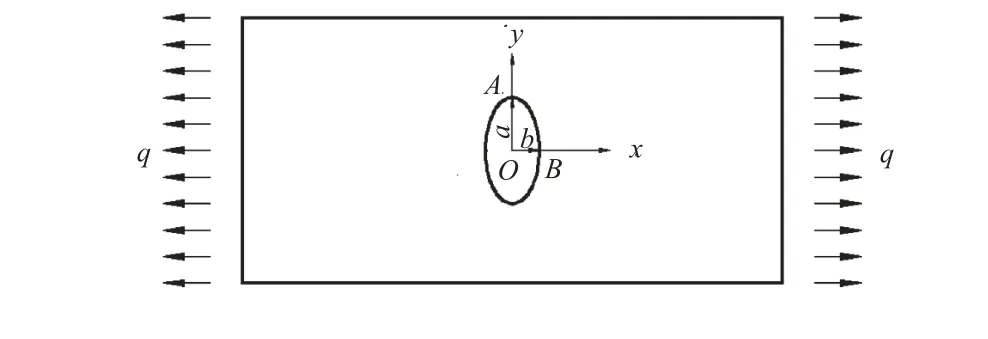
图1 椭圆孔尖端应力集中问题示意Fig.1 Schematic illustration of stress concentration at the tip of an elliptic hole

在有限元计算中，模拟无限大板的四边形尺寸以及网格划分对计算结果有重要影响[6]．本文经试算选定边长为 400,mm×200,mm 的四边形模拟无限大板(1/4对称部分)．建立了椭圆形孔洞的二维计算模型，如图2所示．在该模型中，点O为坐标原点，OA＝20,mm, 计算时 OA的长度固定不变，通过 OB的长度逐渐减小即增大λ值来改变椭圆的形状．

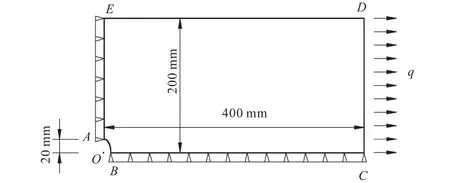
图2 计算模型Fig.2 Calculation model

模型分3种区域进行网格划分：远离 A点区域(Ⅰ)，椭圆弧 AB 附近区域(Ⅱ)，临近 A点区域(Ⅲ)．Ⅰ区域网格边长为 4,mm 左右；Ⅱ区域网格边长为 1,mm 左右；对Ⅲ区域网格进行多级加密，临近A点处网格边长最小处达到 0.001,mm．各区域间网格大小逐渐过渡．根据 Saint-venant 原理，远离 A点处网格的疏密情况对 A点应力影响极小．模型约有1.4×104个单元．图3用全图方式展示了椭圆孔周围网格划分情况．

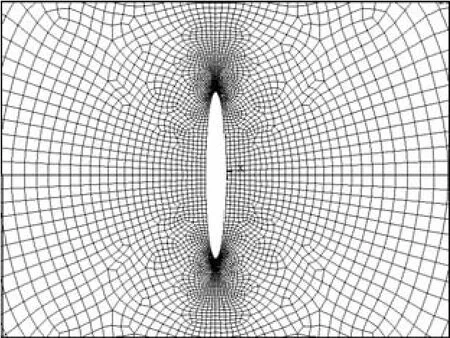
图3 未填充情况下椭圆孔洞周区网格划分(λ＝8)Fig.3 Finite element mesh around the elliptic hole in hollow case (λ＝8)

计算模型的位移边界条件为：①边 OE，Ux＝0；②边 OC，Uy＝0．力的边界条件是：边 CD，均布拉力q＝100,N/mm，其余边为自由边界．

板的弹性模量取0E＝2.5×104,MPa，泊松比取0.25．软性填充物的弹性模量为周围介质弹性模量的0.001倍，泊松比取 0.3．在界面处，软性填充物与周围介质共用节点．

本文的计算重点在于探讨软性填充物以及椭圆形状对椭圆周区应力分布的影响，在计算过程中，假定材料一直处于弹性阶段，暂不考虑材料本构关系的变化对应力分布的影响．

2 计算与分析

含椭圆形孔洞的无限大板在单轴拉伸作用下，A点的应力集中系数具有解析解，即

根据式(1)可计算出不同λ值下的应力集中系数k，采用本模型计算的应力集中系数为1k，软性填充物填充后计算值为2k，见表1.

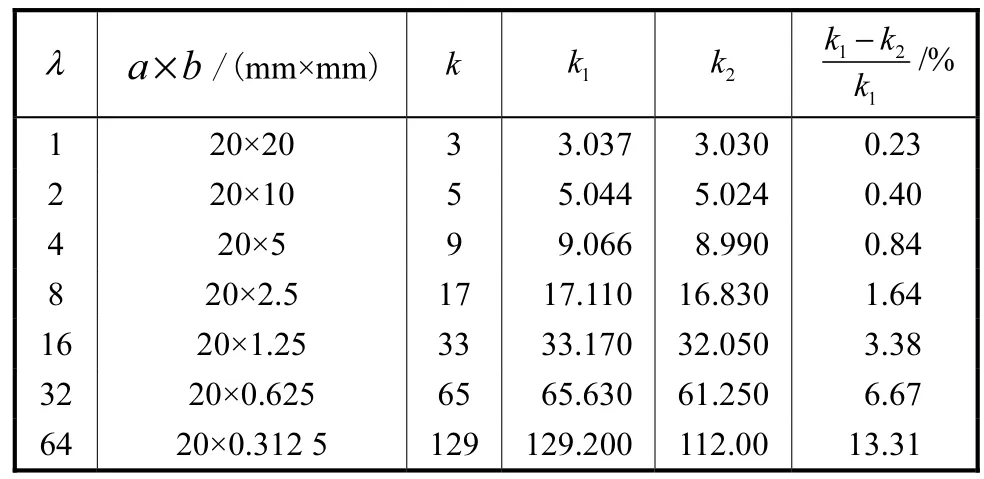
表1 应力集中系数Tab.1 Stress concentration factors

通过与解析解进行比较，衡量此模型的计算误差．模型的相对误差计算式为

根据式(2)可计算出模型的平均相对误差为0.73%，比较可靠．软性填充物对应力集中系数的降低作用随椭圆长短轴之比的增大逐渐增大，从 0.23%增加到13.31%．

仅以λ取 8时，说明椭圆尖端区域应力分布情况，其应力分布等值线图如图4和图5所示．由两图可以发现，由于采取了多级加密的网格划分方案，当趋于椭圆尖端时，等值线趋于光滑，单元应力急速增加，等值线由椭圆尖端向四周呈椭圆形扩散．采用软性填充物填充后，最大应力有一定程度的降低．

沿x轴(OC)方向拉应力xσ的分布计算结果如表2和表3所示．

图4 未填充情况下椭圆尖端应力分布等值线图(λ＝8)Fig.4 Stress contour near the tip of the elliptic hole in hollow case(λ＝8)

图5 填充后椭圆尖端应力分布等值线图(λ＝8)Fig.5 Stress contour near the tip of the elliptic hole in filled case(λ＝8)

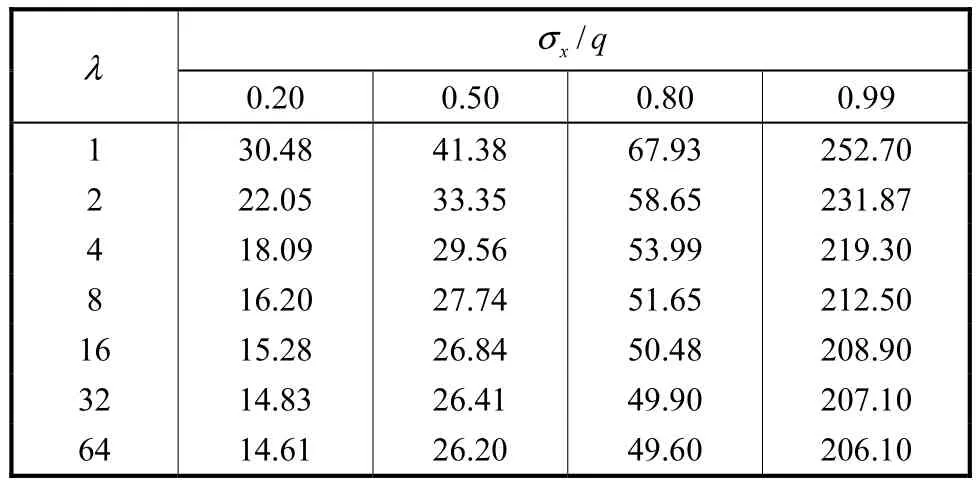
表2 未填充时λ对沿OC方向的xσ的影响范围Tab.2 Influence of λon the distribution of xσ along OC direction in hollow case mm

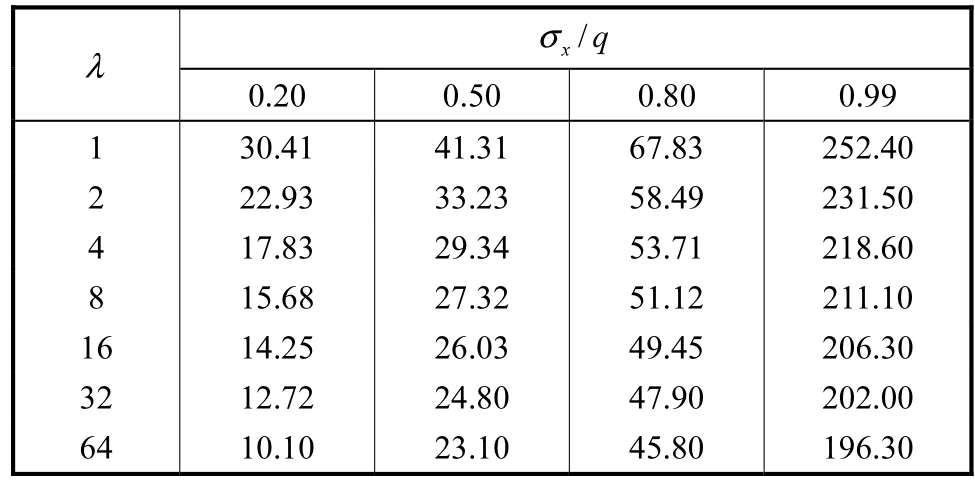
表3 填充后λ对沿OC方向的xσ的影响范围Tab.3 Influence of λon the distribution of xσ along OC direction in filled case mm

表4 未填充时椭圆孔对沿OE方向的xσ的影响范围Tab.4 Influence of the elliptic hole on the distribution of xσ along OE direction in hollow case mm

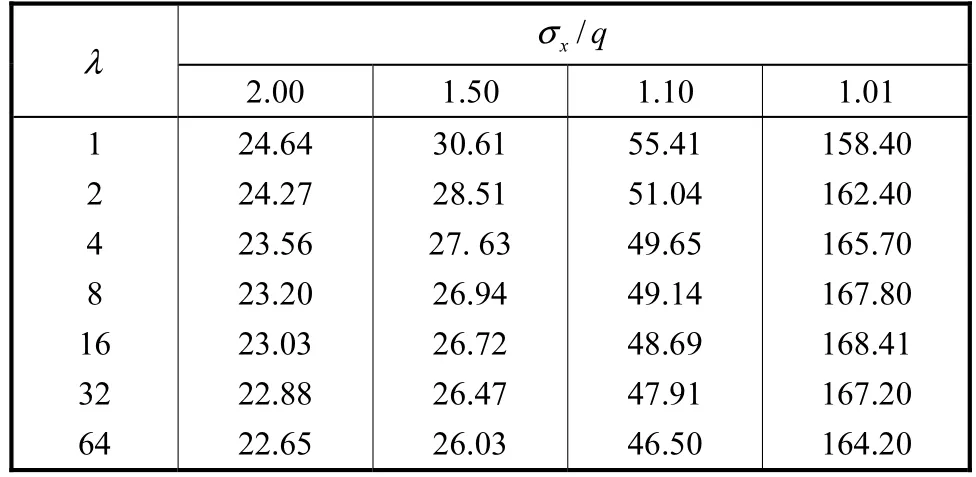
表5 填充时椭圆孔对沿OE方向的xσ的影响范围Tab.5 Influence of the elliptic hole on the distribution of xσ along OE direction in filled case mm

当用弹性模量为周围介质弹性模量0.001的软性物质填充后，上述3个幅值改变为：8.08% (＞6.24%)，16.08%(＞10.74%)，3.66%(＜8.20%)．这说明软性填充物能够使第一阶段应力更迅速降低，使第二阶段中σx趋于q时所用的距离减小．即软性填充物减小了椭圆孔洞对沿OE方向的σx的影响范围．填充前后相比较，σx/ q取1.01、当椭圆长短轴之比为64时，影响范围从 171.5,mm减小到 164.20,mm，降低了4.26%．

软性填充物对第一阶段的沿OC和OE 2个方向的xσ的影响示意如图6所示．

在未填充和填充后2种情况下，沿OE方向的xσ的分布情况如图7和图8所示．由图7和图8可以发现，两图中沿OE方向的xσ的分布形式基本相同，由此可知，虽然填充前后xσ在绝对值上有变化，但填充前后各点处的相对比值变化较小．2种情况下，沿OC方向xσ的分布情况如图9和图10所示．

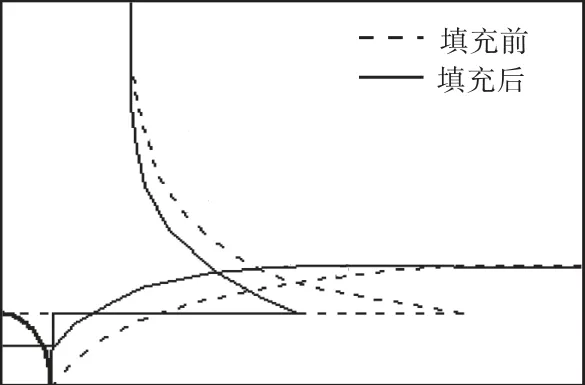
图6 第一阶段沿OE和OC方向的xσ的分布示意Fig.6 Sketch of the distribution of xσ along OE and OC directions in the first stage

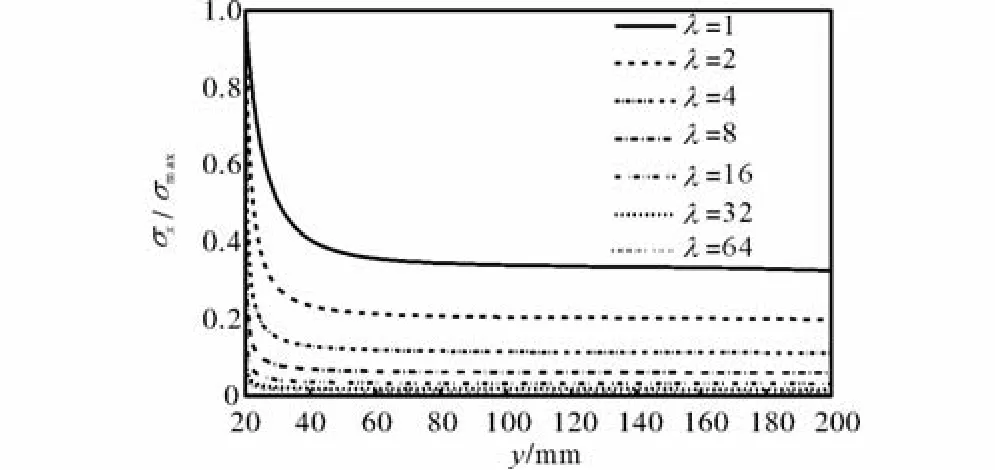
图7 未填充情况下沿OE方向xσ的分布Fig.7 Distribution of xσalong OE direction in hollow case

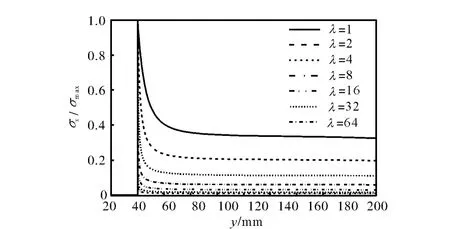
图8 填充情况下沿OE方向xσ的分布Fig.8 Distribution of xσalong OE direction in filled case

由图9和图10可以发现，填充后，随着椭圆长短轴之比的增加，填充物的拉应力xσ′逐渐增大．在计算结果中提取y＝0处填充物的拉应力，如图11所示．当λ为64时，xσ′增加到q的12.68%．这样，在椭圆形孔洞处，通过软性填充物传递的力逐渐增加，即椭圆形孔洞越趋于裂缝，软性填充物所发挥的作用越大．这也是软性填充物能显著降低应力集中系数，降低孔洞对周区应力场影响范围的主要原因．

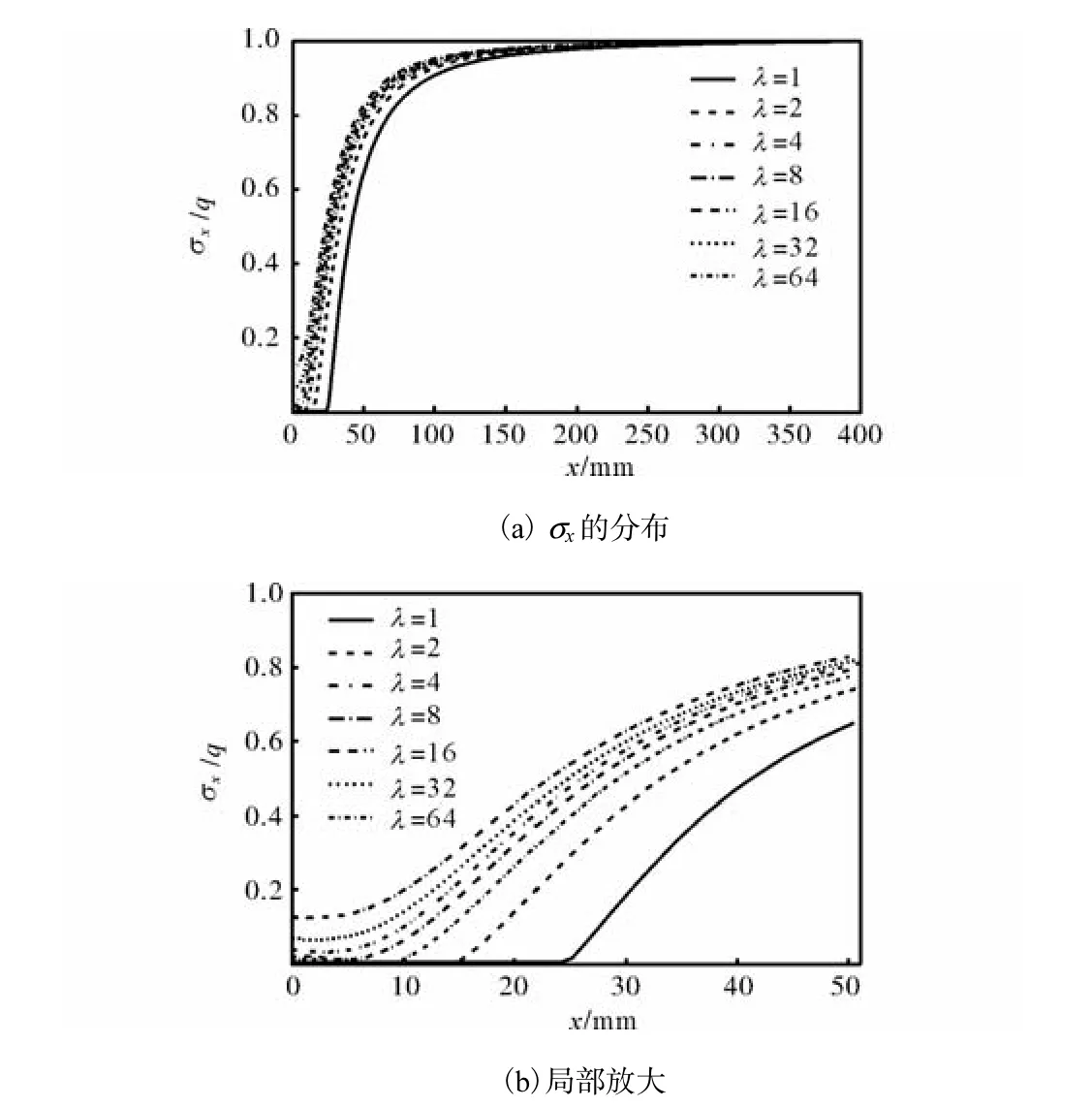
图10 填充情况下沿OC方向xσ的分布Fig.10 Distribution of xσalong OC direction in filled case

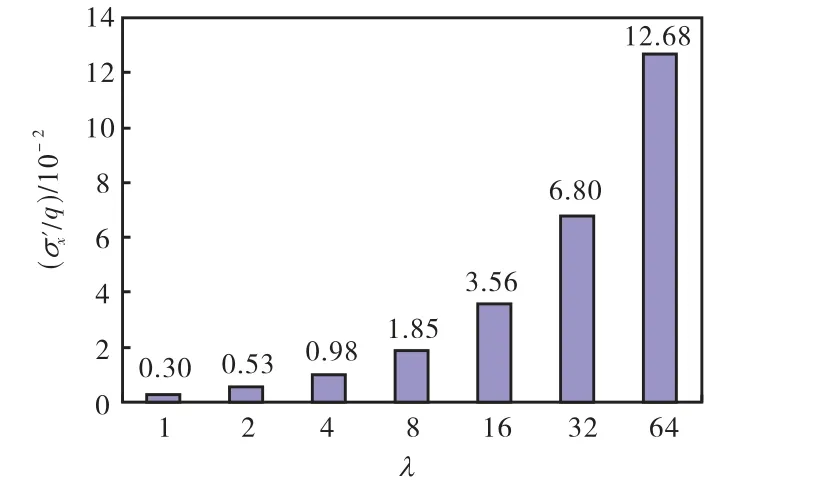
图11 y＝0处λ对′xσ的影响Fig.11 Influence ofλon ′xσwhen y＝0

3 结 语

含椭圆孔洞的无限大板在单轴拉伸作用下，在椭圆孔洞尖端存在应力集中，椭圆孔洞对周区拉应力的分布产生重要影响．随着椭圆长短轴之比增大，应力集中系数逐渐增大，沿 x轴(OC)方向的影响范围逐渐减小，沿y轴(OE)方向的影响范围逐渐增大．当椭圆孔洞被弹性模量为周围介质 0.001倍的软性填充物填充后，应力集中系数显著降低，沿 x轴方向和 y

轴方向的影响范围也明显减小．软性填充物所承受的拉应力随椭圆长短轴之比的增加逐渐增加．综上所述，软性填充物对降低应力集中现象效果十分显著．椭圆越趋于裂缝，软性填充物所发挥的作用越大．本文仅进行了软性填充物弹性模量为周围介质弹性模量的 0.001倍的研究，其他比值的情况有待进一步进行系统的研究．

［1］ 萨文Г H. 孔附近的应力集中[M]. 北京：科学出版社，1958.

Saven Г H.Stress Concentration Around Holes[M]. Beijing：Science Press，1958(in Chinese)．

［2］ Kubair D V，Bhanu-Chandar B. Stress concentration factor due to a circular hole in functionally graded panels under uniaxial tension[J]International Journal of Mechanical Sciences，2008，50(4)：732-742.

［3］ Bakhshandeh K，Rajabi I，Rahimi F. Investigation of stress concentration factor for finite-width orthotropic rectangular plates with a circular opening using threedimensional finite element model[J]Strojniski Vestnik，2008，54(2)：140-147.

［4］ 航空工业部科学技术委员会．应力集中系数手册[M].北京：高等教育出版社，1990.

Committee of Science and Technology of Industry Department of Aviation．Stress Concentration Factor Manual[M]. Beijing：Higher Education Press，1990(in Chinese).

［5］ Guo Wanlin，Dai L，Wang X. Stress concentration at an elliptic hole in transversely isotropic piezoelectric solids[J]. International Journal of Solids and Structures，2006，43(6)：1818-1831．

［6］ Dumir P C. Stress concentration around elliptical holes in a rectangular plate[J].Arabian Journal for Science and Engineering，1998，13(1)：109-112.

［7］ Hanus J B，Burger C P. Stress-concentration factors for elliptical holes near an edge[J].Experimental Mechanics，1981，21(9)：336-340．

［8］ Hebel Jochen，Becker Wilfried. Numerical analysis of brittle crack initiation at stress concentrations in composites[J].Mechanics of Advanced Materials and Structures，2008，15(6/7)：410-420.