质心运动定理与柔绳问题

赵 坚 李 力

(1.昆明市五华区教师进修学校,云南 昆明 650031;2.重庆清华中学,重庆 400054)

1 引言

变质量物体的动力学问题是力学里一个重要的问题,而各种柔绳问题则是其中的典型例子.通常解决柔绳问题有三种思路:一是应用质点组的动量定理求解;二是应用根据质点组的动量定理推导出的变质量物体运动方程——密歇尔斯基方程求解[1];三是应用变质量质点的动能定理求解[2].这些方法有一个共同特点,都需要认真选取研究对象(往往有三种甚至更多的选取方案[3]),弄清楚它由哪些部分组成,并且明确各部分并入(或分离)前后的初、末速度,才能正确地求解柔绳问题,一般情况下这些方法都比较烦琐而且容易出错.

笔者以为求解柔绳问题更为方便简捷的方法是应用质点组的质心运动定理.质心运动定理的表达式为maC=F外,其物理意义是:将全部质量与外力平移到质心上,合成总质量m和合外力F外,质心就与一个在力F外作用下质量为m的质点做相同的运动[4].现在我们用它来分析常见的各种柔绳问题.

2 水平拉绳问题

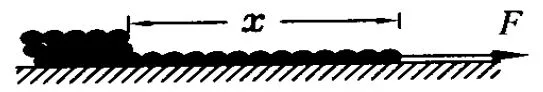
图1

如图1,长为L、线密度为λ的匀质柔绳盘在光滑水平面内,现用一水平力F作用于绳端,在下列三种情况下,分别求出拉力F的大小.

(1)以恒定速度v拉动绳端.

(2)绳端从静止开始以恒定加速度a运动.

(3)假设地面粗糙,绳与地面间的动摩擦因数为μ,以恒定速度v拉动绳端.

解析:(1)取全部柔绳为研究对象,如图1所示,以绳端出发点为原点,当拉动部分的绳长度为x时,其质心坐标根据质心运动定理得F=λLaC=λv2,可见在光滑水平面上匀速拉动绳端时的拉力是一个大小为λv2的恒力.反之可以看出,在光滑水平面上用恒力F拉绳端,则绳端必然做速度为的匀速运动.

(2)xC、vC与(1)中相同,此时根据质心运动定理得到这个拉力是与t2成正比或者说与x成正比的变力.反之,在光滑水平面上用与拉出距离x成正比的水平力拉动静止绳的一端,绳端必然做加速度为的匀加速直线运动.

(3)xC、vC、aC都与(1)中相同,由质心运动定理得到所以这是一个随时间线性变化的力.

3 竖直提绳问题

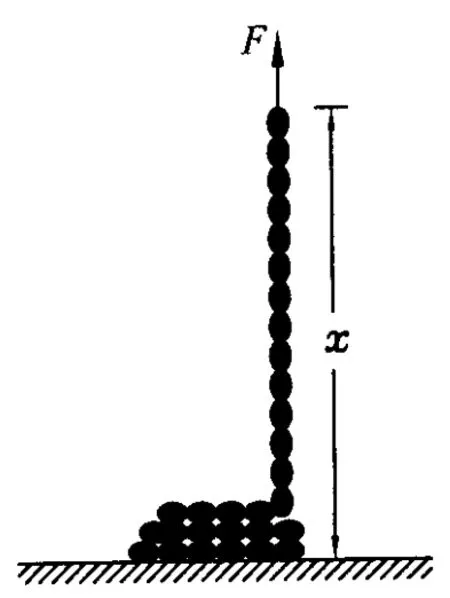
图2

长为L、线密度为λ的匀质柔绳盘在光滑水平面内,现用一竖直向上的力F作用于绳端,以恒定速度v提起绳子(如图2),求拉力F的大小.

解析:取整个柔绳为研究对象,当拉起部分的长度为x时,从水平拉绳问题的(1)中可知质心的加速度整段绳子所受外力为F-λxg,由质心运动定理得到F-λxg=λL◦aC=λv2,即F=λv2+λxg=λ(v2+gvt).

其实,这种情况与水平拉绳的第(3)问中绳子所受阻力正比于拉出距离x相似,据此可用类比方法写出相应的答案.

4 竖直落绳问题

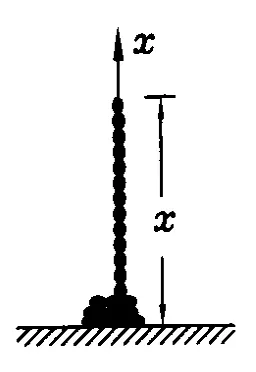
图3

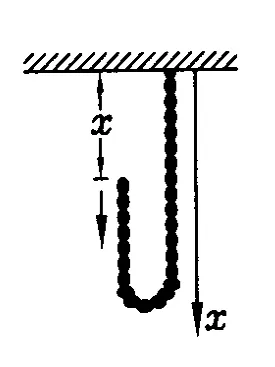
图4

(1)如图3,长为L、线密度为λ的匀质柔绳竖直地悬挂着,其下端刚好与地面接触.此时放开上端,使它从静止开始自由下落,求空中绳长为x时,地面对绳子的作用力F.

(2)如图4,长为L、线密度为λ的匀质柔绳对折后,将两端竖直地悬挂在天花板上,然后由静止开始释放一端使其自由下落,求释放端下落x时天花板对绳的拉力F.

解析:(1)取整个绳子为研究对象,设留在空中的绳长为x且以向上为正方向,此时质心的坐标为xC,vC与水平拉绳问题(1)中相同,而其中代入质心运动定理得这个力正好等于已经落在地上绳子重力的3倍[4].(编者注是绳子上端下落速度,对于匀质柔绳,它和自由质点下落速度相同,所以有就是绳子上端下落的加速度.)

(2)取整个绳子为研究对象,以悬挂点为原点且向下为正方向,质心的坐标、速度、加速度分别如下:

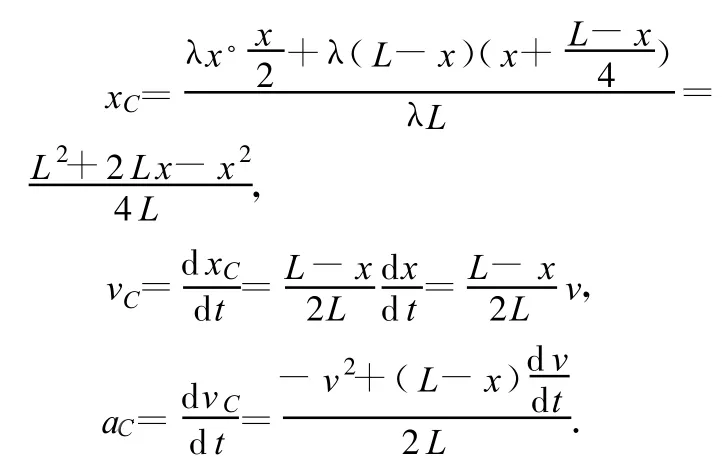
5 结束语

从上述可以看出,用质心运动定理求解柔绳问题时,选择整个绳子为研究对象,这样就把变质量物体转化为定质量问题了,而且只考虑外力,不需要分析内部各部分间的相互作用,也不需要分析各部分并入(或分离)前后的运动情况,所以相对其他方法而言,应用质心运动定理解决柔绳问题是比较方便、简捷的.

1 周衍柏.理论力学教程(第2版).北京:高等教育出版社,1986.137

2 石东平.变质量质点的动能定理与软绳问题.大学物理,1999(3):22

3 钱天虹,何锃.变质量物体运动方程与落链问题.物理通报,1997(11):1

4 赵凯华,罗蔚茵.新概念物理教程◦力学(第2版).北京:高等教育出版社,2004.125

5 肖士王旬.理论力学简明教程.北京:人民教育出版社,1979.128