高密度相位光栅的偏振选择性
王 博
(广东工业大学物理与光电工程学院,广东广州510006)
高密度相位光栅的偏振选择性
王 博
(广东工业大学物理与光电工程学院,广东广州510006)
高密度光栅具有与传统光栅不同的性质,其衍射特性往往是偏振相关的。本文针对1 550 nm波长TE/TM偏振入射光和0.5的光栅占空比,利用严格耦合波分析数值计算了不同光栅周期下0级及-1级的衍射效率。研究表明,相比周期为1 550 nm的光栅,当周期为1 200 nm时,偏振相关衍射效应明显增强,当光栅周期为890 nm时,TE偏振光的衍射效率随着光栅深度呈正余弦变化,而TM偏振光的衍射效率始终集中在0级,具有偏振选择性。通过模式方法,利用模式中的有效折射率概念,研究了不同周期下被入射光所激发的两种光波模式通过光栅区域传播所累积的相位差;基于双光束干涉,模拟了0级和-1级的衍射效率。结果表明,利用严格耦合波分析的数值计算结果符合模式方法的理论预期,对于高密度相位光栅的偏振选择性给予了合理的物理机制解释。
高密度光栅;严格耦合波分析;模式方法;偏振选择性
1 引 言
衍射光栅广泛应用于许多光学信息处理系统中[1~3]。对于低密度光栅,可以利用标量衍射理论来研究衍射特性,与偏振无关。当光栅的周期达到波长量级或者小于波长时,衍射特性往往是偏振相关的。高密度光栅的衍射特性必须采用直接求解矢量形式的麦克斯韦方程,应用如严格耦合波分析[4]和模式方法[5]等进行分析。与低密度光栅相比较,高密度光栅衍射级次少,入射光的能量可以高度集中,并且具有新颖的衍射特性,能够设计新型的微光学器件。近来,一些研究工作报道了基于熔融石英高密度深刻蚀光栅来实现密集波分复用[6]、偏振器[7]、分束器[8]。对于高密度光栅的衍射特性的计算可以利用严格耦合波分析,其反射、透射、偏振和光谱结构等与常规光栅截然不同。然而,从这些数值结果很难理解发生在光栅区域内部的物理机制。Clausnitzer等人把模式方法[5]应用在高效率电介质透射光栅中,给出了合理的物理解释[9],并研究了对于特殊占空比0.51的偏振相关衍射[10]。
本文研究了高密度相位光栅对于常规占空比0.5的偏振选择性。在TE/TM偏振光入射下,对于不同光栅周期,数值计算了衍射效率随着光栅深度的变化关系。在优化的光栅周期下,得到高密度光栅的偏振选择性。通过模式方法,利用光栅区域中被入射光激发的模式的有效折射率解释了其物理机制。
2 严格耦合波分析计算
图1示出了高密度透射光栅的几何结构,其中n1和n2分别是空气和光栅介质的折射率,d为周期,b和g分别为突起和凹槽的宽度,h为深度,占空比f定义为光栅凸起宽度与周期的比值。波长为λ的线性偏振光以布拉格角θi=arcsin(λ/2d)入射到光栅上。根据光栅方程,高密度光栅仅考虑有0和-1级两个衍射级次存在。
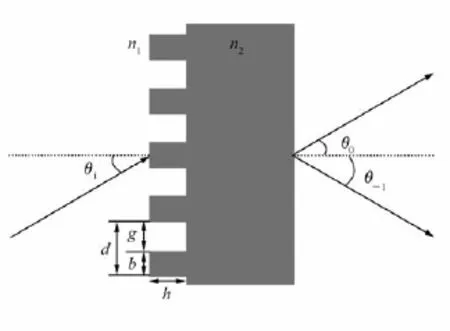
图1 高密度透射相位光栅示意图
图2示出了不同光栅密度下,利用严格耦合波分析计算的透射光栅的衍射效率与深度的关系曲线,其中光栅突起石英的折射率n2=1.444 62,入射光的波长为1 550 nm,占空比为0.5。可以看出,随着密度增加,光栅表现出了很强的偏振相关衍射特性。如图2(a)所示,对于周期在波长附近的光栅,TE/TM偏振光的效率随着深度近似于正余弦变化。两种偏振光的衍射特性有所不同,这是在低密度光栅中所不能预期的。如图2(b)所示,当周期减小为1 200 nm时,TM偏振光效率的变化周期显著增大,偏振相关衍射效应进一步增强。如图2(c)所示,当周期减小至890 nm时,不管深度如何变化,TM偏振光的效率主要集中在0级,TE偏振光的衍射效率仍然随着深度正余弦变化,光栅对于两种偏振光的衍射具有截然不同的性质。但是从这些数值结果中,并不能得到清晰的物理解释。

图2 利用严格耦合波分析计算的熔融石英光栅的衍射效率(η)随深度变化的曲线(f=0.5,λ=1 550 nm)
3 模式方法解释
根据模式方法[5],入射光沿着垂直方向通过光栅区域传播时,能够激发一组分立的模式。>0的模式通过光栅区域传播,而这些<0的模式变为倏逝波。随着光的传播,倏逝波的振幅迅速减少,在深刻蚀光栅情况下,可以忽略倏逝波的模式。对于TE偏振光,被激发模式的有效折射率满足如下方程[5]:
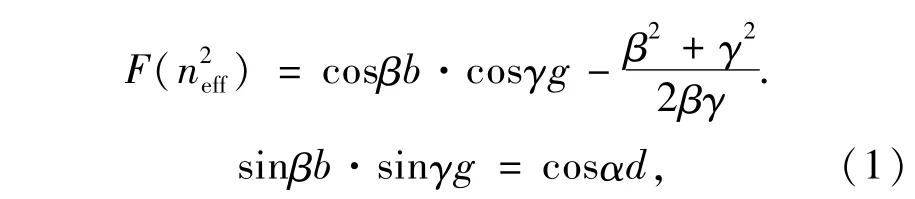
对于TM偏振光:

其中:

式中,εb和εg分别为光栅突起和凹槽的介电常数。
对于高密度深刻蚀偏振分束光栅,模式方法可以把复杂的衍射过程简化为由入射光所激发的两个模式的双光束干涉。具有不同有效折射率的两个模式通过光栅区域传播,在光栅基底界面耦合出来[9]。传播距离(即光栅深度)和有效折射率决定了累积的相位差,两个模式在光栅基底界面的相位差Δφ可以表示为:

在两个模式的干涉过程中,相位差将会对0和-1级的衍射效率起着主要的作用。一方面,当相位差为π的奇数倍时,-1级将有着较高的衍射效率;另一方面,当相位差为π的偶数倍时,0级将有着较高的衍射效率。

图3 不同周期下,F()的特征值关系(f=0.5,λ=1 550 nm)

图4 基于两个模式的双光束干涉,衍射效率随着光栅深度的变化曲线(式(7),(8))(f=0.5,λ=1 550 nm)
再者,可以利用入射波所激发的两个模式的干涉来模拟计算衍射效率。对于模式0,光栅区域中的归一化电场可以表示为:
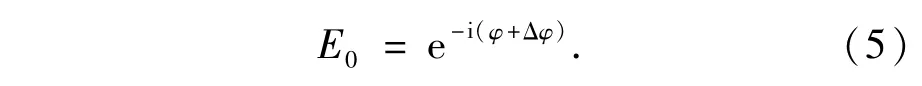
对于模式1:
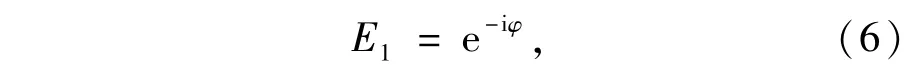
其中φ为模式1的相位。因此,0级的衍射效率为:

根据能量守恒定律,-1级的衍射效率可以表示为:
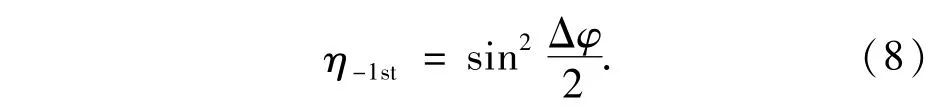
利用两个模式干涉(式(7),(8)),可以计算TE/TM偏振光的衍射效率,如图4所示。比较图2和图4,利用严格耦合波分析得到的数值结果和基于模式方法的模拟计算符合得非常好。
4 结 论
高密度光栅具有偏振相关衍射效应。严格耦合波分析表明,占空比为0.5的石英光栅周期为890 nm时,1 550 nm波长TE偏振入射光的衍射效率随着光栅深度呈正余弦变化,而TM偏振光的衍射效率始终集中在透射0级,具有偏振选择性,这是标量衍射理论所不能预期的。通过模式方法,利用模式中的有效折射率的概念,计算了被入射光激发的两种光波模式通过光栅区域传播所累积的相位差,根据双光束干涉解释了高密度光栅的偏振选择性。本文中对高密度相位光栅偏振选择性的计算和解释将有助于理解光在光栅区域的传播过程和设计微光学器件。
[1]周素梅,周常河.二次光栅在波前测量中的应用[J].光学学报,2007,27(1):1-4.
ZHOU SM,ZHOU CH H.Wavefrontmeasurement by using quadratic grating[J].Acta Optica Sinica,2007,27(1):1-4.(in Chinese)
[2]底彩慧,周常河.基于达曼光栅的动态光耦合器[J].光学学报,2007,27(7):1275-1278.
DICH,ZHOU CH H.Dammann grating-based dynamic optical coupler[J].Acta Optica Sinica,2007,27(7):1275-1278.(in Chinese)
[3]ZHENG J J,ZHOU CH H,DAIEW.Double-line-density gratings structure for compression and generation of double femtosecond laser pulses[J].J.Opt.Soc.Am.B,2007,24(4):979-984.
[4]MOHARAM M G,GRANN E B,POMMETD A,et al..Formulation for stable and efficient implementation of the rigorous coupled-wave analysis of binary gratings[J].J.Opt.Soc.Am.A,1995,12(5):1068-1076.
[5]BOTTEN IC,CRAIGM S,MCPHEDRAN R C,et al..The dielectric lamellar diffraction grating[J].Opt.Acta,1981,28(3):413-428.
[6]WANG SH Q,ZHOU CH H,ZHANG Y Y,et al..Deep-etched high-density fused-silica transmission gratings with high efficiency at a wavelength of 1550 nm[J].Appl.Opt.,2006,45(12):2567-2571.
[7]WANG B,ZHOU CH H,WANG SH Q,et al..Polarizing beam splitter of a deep-etched fused-silica grating[J].Opt.Lett.,2007,32(10):1299-1301.
[8]FENG JJ,ZHOU CH H,ZHENG JJ,etal..Dual-function beam splitter ofa subwavelength fused-silica grating[J].Appl.Opt.,2009,48(14):2697-2701.
[9]CLAUSNITZER T,KÄMPFE T,KLEY E-B,etal..An intelligible explanation of highly-efficient diffraction in deep dielectric rectangular transmission gratings[J].Opt.Express,2005,13(26):10448-10456.
[10]CLAUSNITZER T,KÄMPFE T,KLEY E-B,et al..Investigation of the polarization-dependent diffraction of deep dielectric rectangular transmission gratings illuminated in Littrow mounting[J].Appl.Opt.,2007,46(6):819-826.
Polarization-selectivity of high-density phase gratings
Wang Bo
(School of Physics and Optoelectronic Engineering,Guangdong University of Technology,Guangzhou 510006,China)
Diffraction properties of high-density gratings are polarization-dependent,which are different from those of conventional gratings.For TE-and TM-polarized incidentwaveswith a wavelength of1 550 nm and a duty cycle of 0.5,diffraction efficiencies in the 0th and-1st orders are calculated using Rigorous Coupledwave Analysis(RCWA).It indicates thatmore polarization-dependent characteristics are shown for the period 1 200 nm compared with 1 550 nm.Especially,with the period 890 nm,the diffraction efficiency of TE-polarized wave changeswith grating depth sinusoidally,while the efficiency of TM-polarized wave which has polarization-selectivity is always concentrated on the 0th order.According tomodalmethod,modes excited by the incidentwave are investigated for different periods and the accumulated phase differences of the two modes with different effective indices are calculated when they propagate through the grating region.Moreover,diffraction efficiencies in the 0th and-1st orders are simulated based on two-beam interference.Experimentalresult shows that the numerical calculation resultusing RCWA coincideswellwith the theoretical predictions of modalmethod,which can explain the physical mechanism of polarization-selectivity of high-density phase gratings.
high-density grating;Rigorous Coupled-wave Analysis(RCWA);modal method;polarization-selectivity
O436.3
A
1674-2915(2010)04-0348-05
2010-01-11;
2010-03-13
广东省自然科学基金资助项目(No.9451009001002756);广东省教育厅优秀青年创新人才培育项目(育苗工程)(No.100068)
王 博(1980—),男,山东济宁人,讲师,博士,主要从事新型微光学元件的设计和制作。
E-mail:wb_wsx@yahoo.com.cn

