基于Mie散射的CO2激光大气传输特性测量

张合勇，王挺峰，邵俊峰，赵 帅，郭 劲

（中国科学院长春光学精密机械与物理研究所，激光与物质相互作用国家重点实验室，吉林长春130033）

基于Mie散射的CO2激光大气传输特性测量

张合勇，王挺峰，邵俊峰，赵 帅，郭 劲

（中国科学院长春光学精密机械与物理研究所，激光与物质相互作用国家重点实验室，吉林长春130033）

为了更准确地计算大气透过率，在Mie散射理论基础上，分析了雷达系统设计中需考虑的大气透过率的经验计算公式，指出了该经验公式的不足。考虑大气分析软件MODTRAN自身的优点，采用经验公式和软件计算相结合的方式计算大气透过率，给出了MODTRAN计算结果的修正表达式。在该理论指导下，进行了CO2激光大气传输实验。由于没有考虑大气湍流，理论计算和实验结果存在一定偏差，但不影响本文方法的实用性。实验测量显示，激光器出口处光斑能量抖动比为6.18％，而在50 m和1 km处能量抖动比分别为8.3％和50.2％，表明随着传输距离增加，能量抖动比增大。除掉激光器本身输出能量抖动外，在50 m和1 km处由大气传输造成的能量抖动比分别为2.12％和44.02％。实验结果提示，水平传输1 km时能量抖动已相当剧烈，所以对更远距离的激光传输，自适应光学补偿显得尤为重要。

大气传输；Mie散射；MODTRAN软件；CO2激光；能量抖动比

1 引 言

激光在大气中传输会受到气溶胶的折射、吸收、散射、湍流、热晕等综合作用而引起激光束能量的衰减和空间分布的改变，从而影响系统的性能和精度。低能激光作用下，大气湍流占优势；高能激光作用下，热晕引起的畸变变得很突出［1～2］。在低矮或湿度较大的大气中，大气的吸收、散射、湍流作用都较强，较强的吸收、散射、湍流作用将增加热晕效应的影响；而在干燥洁净大气中，大气的吸收、散射、湍流、热畸变效应都将明显减弱，所以选择高空进行激光发射和通讯是较理想的。地面光电设备同样涉及激光在大气中传输的影响，比如激光主动照明成像，无论采用可见或红外光波，在大气中传输都会造成不同程度的吸收和散射。系统用激光器作为照明光源辐射照明目标，利用接收系统来接收探测目标反射回的光辐射并最后成像。主动成像的工作方式克服了被动成像系统易受环境光源影响的缺点，尤其适用于在微光、夜视和散射介质中的成像以及远程小暗目标及深空目标的探测成像［3～5］，但主动成像系统中［6］，照明的激光光束和目标回波信号也会在大气传输的过程中受大气衰减、目标反射、背景辐射和大气悬浮微粒后向散射的干扰而严重影响系统性能，降低了系统的成像质量。因此，在设计激光测距及跟踪系统时，都需要考虑激光在大气中的传输和衰减［7～9］，以得到在要求作用距离下所需的激光发射功率。传统的计算大气透过率的方法是采用经验公式，该公式主要考虑气溶胶散射（Mie散射）。因为对于波长较长的红外激光而言，Mie散射比瑞利散射强几个数量级，而衰减主要是由散射造成的，所以主要考虑Mie散射即可。然而该经验公式存在以下不足：（1）只是将所有天气条件的影响因素归结为能见度的简单表述，缺少符合实际条件的可调节参量。（2）所用的探测波长，几乎都位于大气透射窗口位置，但在不能兼顾这一标准的情况下，可能波长正好不处在透过率窗口最高位置，由此会带来误差。（3）经验公式不能求取斜程的大气透过率，这对系统设计而言不够准确。因此，本文在Mie散射理论基础上，提出采用经验公式和MODTRAN相结合的改进方法。单纯的MODTRAN只能提供几个典型的能见度取值，而经验公式取值不受限制，二者可以弥补各自不足。在此基础上，本文还进行了CO2激光大气传输实验，得到了初步实验结果。

2 Mie散射理论基础

图1 沿x方向偏振的光散射图

如图1所示，沿x方向偏振光经过球形粒子散射后可以分解为垂直和平行于散射面的两个分量。

由经典Mie散射理论，两个方向振幅的分量分别为［10～12］：

在振幅函数的表达式中：

在振幅函数的表达式中，系数an和bn与球形散射粒子的尺度参数α＝2πa/λ和折射率m有关，并表示为：

且有递推公式：

其中z为变量，Jn+1/2（z）和Yn+1/2（z）分别为半整数阶的第一类，第二类贝塞尔函数。由前文所计算的两个振幅函数可以得出微分散射截面表达式：

将微分散射截面对全空间立体角积分可得散射截面表达式：

在雷达系统设计中，需要计算Mie散射消光截面，单个球形粒子消光截面的表达式为：

考虑单位体积内所有粒子的消光截面（体消光截面）时，只要对气溶胶粒子尺度谱进行积分即可，而尺度谱可由下式给出：

式中rbar为粒子体系的几何平均半径，σ为粒子体系几何标准偏差，N为单位体积的粒子数。

由此可得体消光截面：

由式（9）和（11）可以看出，要计算微分散射截面和消光截面首先必须计算散射光的两个相互垂直分量的振幅函数s1（θ）、s2（θ）以及系数an、bn，而由式（1）看出两个振幅函数与系数an、bn、πn、τn都有关，因此，最终需计算的量只有an、bn、πn、τn。下面重点讨论这4个系数的数值计算实现。散射物理参量具体初始条件为：

通过设定符号变量x和两个符号函数ψn（x）和ξn（x），对于ψn（x）的计算可直接根据式（5）运用Matlab自带函数Besselj来实现；对于ξn（x）的计算直接根据式（6）运用Matlab自带函数BesselJ和BesselY的组合来实现；由于初值已经给出，所以两个导数项ψ′n（x）和ξ′n（x）分别用前面已经求出来的ψn（x）和ξn（x）根据递推式（7）和（8）得出；由此只需要运用Matlab自带函数Inline和Vectorize将符号变量和符号函数转化为数值变量和数值函数。代入数值变量α和mα就可以分别计算出 ψn（α），ψn（mα），ψ′n（α），ψ′n（mα），ζn（α），ζn（mα），ζ′n（α），ζ′n（mα），代入（4）式就分别可以求出an和bn。πn和τn可以由Matlab自带Legendre函数得出，其准确性可以由非偏振情况下单个粒子散射相位函数的图像得到，和参考文献中的图形完全符合。

根据散射系数，消光系数计算公式：

其中α＝2πa/λ，a为球形粒子的半径（散射截面与散射系数之间相差一个常数就是粒子的几何截面πa2）。图2为折射率为1.33的球形粒子消光系数与粒子尺度参数关系。

图2 球形粒子消光系数

由图2可知，当粒子半径比激光波长小很多时，消光系数随着波长的缩短而迅速增加，直到粒子半径a≈0.9λ，消光系数达到最大值3.8。随着比值a/λ的进一步加大，消光系数做衰减振荡变化，但对于足够大的a/λ值，消光系数趋近于2，并且与波长几乎无关。

3 大气透过率的近似计算

激光在大气中传输时，除了受到选择性吸收以外，还会发生散射作用，纯散射不引起激光光束总能量的损耗，但会改变激光光束能量原来的空间分布，所以经散射后，会导致原来传播方向上激光光束能量的衰减。对于波长为λ的单色激光光束，在不均匀媒质内传播距离x后，由于纯散射作用，将使激光沿x方向的衰减为［13］：

式中Pλ（0）和Pλ（x）分别为在散射前和经过x距离散射后的单色激光光束功率；γ（λ）为散射系数，因而纯散射所决定的媒质透过率为：

一般情况下，大气中的散射由两类散射元组成，即大气分子散射和大气中悬浮微粒（气溶胶）散射，所以上式中的散射系数可以分为以下两项之和：

其中γm（λ）和γa（λ）分别表示分子散射系数和气溶胶散射系数。如能求出散射系数，就可以计算出给定大气路程长度x纯散射透过率τs（x，λ）。对于低空对流层或平流层，对于波长较长激光而言，分子散射几乎可以忽略，所以只需考虑气溶胶散射。而在实际应用过程中，确定大气散射系数的实用方法是测量某一指定波长的气象学距离，进而可以确定大气在任意波长上的透过率，气象学距离定义为人眼对着地平线天空刚好能够看见大的黑色无反射的目标的平均距离（km），为排除人眼视力的差别，严格的定义是指在可见光区指定波长λ0处，通常选取0.55μm处的目标和背景对比度降低到2％时的距离。2％的对比度是人眼刚好能够辨认目标和背景的典型平均值。在指定波长0.55μm处，大气的吸收很少，因而引起激光衰减的原因只有散射一种因素。根据文献［14］中的推导，可以得到散射系数与能见距离Rm（以km为单位）之间的关系为：

当由指定波长λ0处的能见距离求解大气透过率τs时，散射系数γ（λ）是波长的函数，一般而言，对红外激光，瑞利散射不重要，于是有γ（λ）＝Aλ-q，其中q为经验常数，当大气能见度较好时，能见距离Rm＞80 km，则q＝1.6；中等能见度大气时，q＝1.3；对于浓厚的霾，能见度很差，Rm＜6 km，可取q＝0.585。此时，波长为λ0处散射系数的表达方程为：

由此可得：

对任意波长λ，光谱散射系数或纯散射衰减为：

由此可得相应得大气透过率为：

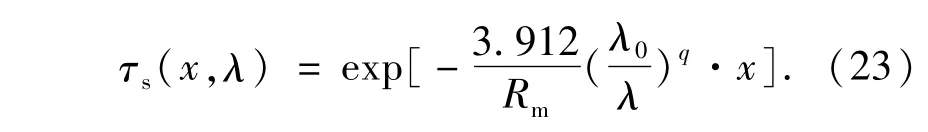
若考虑双程透过率时，相应透过率为：

其中参数q的取值已经在上文中阐述。在所要求的探测距离10 km处，由以上公式可以得到各个能见度下各个波长的大气透过率如图3所示。

图3 不同能见度的透过率

由图3可知，在能见度6 km时，出现跳跃，因为从透过率与能见度的关系可以看出，对于参数q的取值并不连续，分别在6 km和80 km位置处出现跳变，只是图中没有画出80 km的透过率。由此可以看出采用经验公式计算的缺陷。为实现对比，将经验公式计算结果与MODTRAN计算结果进行对比，其中MODTRAN计算参数如下：中纬度冬季沿海平面水平路径，探测距离为10 km，气溶胶选型为乡村能见度23 km，波长覆盖0.3～12μm，频率增量为4 cm-1，计算得到水平路径大气总透过率如图4所示。

图4 水平探测10 km大气透过率

由图4可以得到以下规律：

（1）在波长＜4μm时，经验公式与MODTRAN计算结果符合较好，在远红外波段，二者相差较大。

（2）经验公式只能反映透过率的变化的轮廓，不能反映细节信息，这对于一般的雷达设计影响不大，因为所选取的波长必须位于大气窗口处，而在该位置处，经验公式还是可以作为一个很好的近似。

（3）经验公式只能反映水平路程的透过率，对于斜程路径无法反映出来。为此，将MODTRAN计算的斜程透过率与经验公式计算结果对比如图5所示。

上图MODTRAN计算参数如下：中纬度冬季斜程路径，探测距离为10 km，天顶角为30°，气溶胶选型为乡村能见度23 km，波长覆盖0.3～12μm，频率增量为4 cm-1，由于气溶胶垂直分布，所以在斜向等路径方向气溶胶消光比水平要小，总的透过率要大一些，由图可知，在5μm之前经验公式计算与MODTRAN计算相差较大，在长波红外二者符合较好。

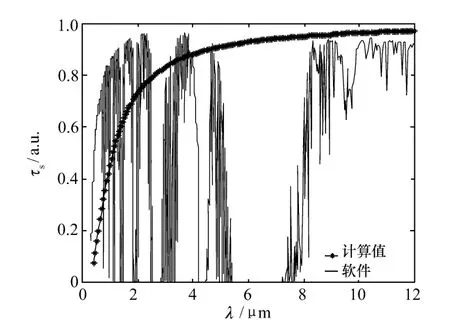
图5 斜程10 km大气透过率

但是，在利用MODTRAN进行计算时，同样存在一个问题，就是软件内部所提供的参数中，能见度只有几个典型值，很多时候该典型值与实际值存在偏差，所以也带来了一定的不确定性，而经验公式却给出了能见度的连续变化关系，这样，可以考虑将经验公式和MODTRAN软件结合起来使用。具体操作如下：首先利用软件计算出和实际测量能见度最接近值处的透过率；然后利用经验公式转化为在实际所需能见度情况下的透过率，如此即可充分结合二者优势。

以MODTRAN中能见度23 km为基础，建立起相邻能见度的透过率值，根据经验公式给出的能见度和透过率之间的关系式，定义23 km能见度位置的大气单程透过率为τs0（x，λ），其它能见度对应的透过率为τs（x，λ），二者之比为：

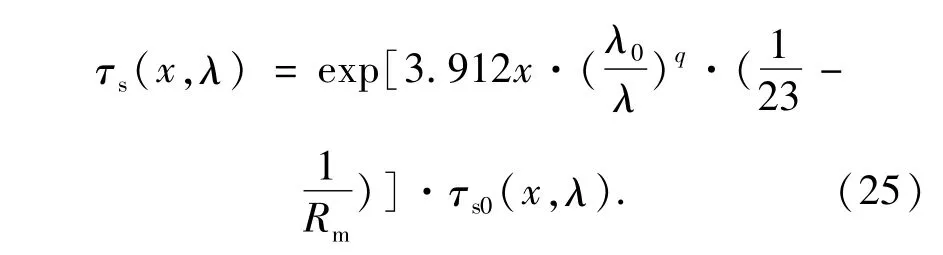
上式中23 km能见度下的透过率可以通过MODTRAN计算得到，其它任意临近能见度下的透过率可以通过上式进行转化。本文以10.6μm激光为例进行了分析，计算条件如下：中纬度冬季水平路径，探测距离为10 km，气溶胶选型为乡村能见度23 km，计算得到10.6μm波长的透过率为0.69，由此可得到在邻近能见度时刻的透过率如图6所示。

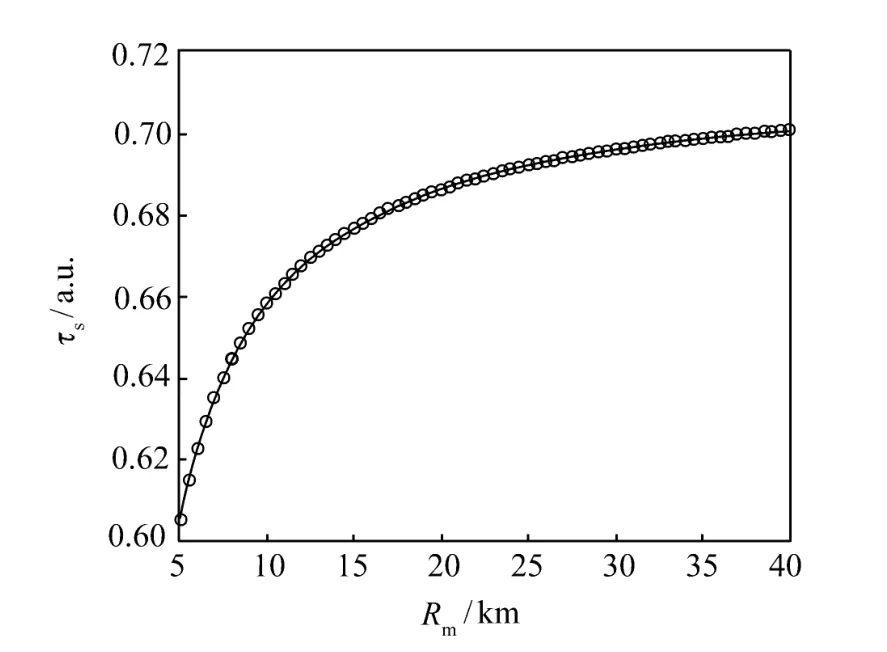
图6 透过率与能见度关系

由图6可知，能见度越大所对应的透过率越大，这是很直观的；随着能见度的加大，透过率增加的速度变慢，最后趋于稳定。

4 激光大气传输实验

为了验证上述理论分析，进行了CO2激光大气传输实验，实验装置如图7所示。

图7 CO2激光传输实验装置

如图7所示，CO2激光器输出光束在自由空间中传播，本实验在空间中不同距离位置测量光斑的能量，由于出口处的光斑为中空矩形，因此衍射之后的多个光斑入射在漫反射屏上，通过红外相机可以拍摄光斑的图样；通过相机采集的光斑图像，可以实现光斑中心的选取，然后即可用能量计探测在指定距离处入射在探测器表面的光能量。取光斑尺寸为2.7 cm×2.7 cm，中间伴随1 cm×1 cm矩形空洞，发散角为1.2 mrad。入口处光斑实际面积为6.29 cm2，能量密度为1.11 J/cm2，并将光斑看作是中空的矩形。对出口处光斑能量进行测量，以便评估激光器的能量稳定性，所测量的出口处光斑能量分布如表1所示。

表1 出口处光斑能量Tab.1 Laser energy of at output w indow

根据多次测量平均的原理，为了反映每一次测量结果偏离平均值的大小，定义样本均方差值如下：

其中样本均值定义为：

定义方差相对于均值的百分比（能量抖动比）为：

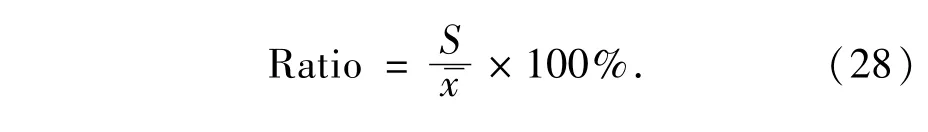
由表2中的数据可计算得出口光斑能量均值为7.2 J，方差为0.445 J，方差与均值之比（能量抖动比）为6.18％，说明光斑出口处能量趋于稳定，可进行远距离光斑能量分布测量。

远距离实验选取6个探测距离，选用了两种不同型号的红外探测器，分别计算在不同距离处的光斑面积，Modtran计算针对能见度5 km时的水平透过率，根据出口处的光斑能量可以计算得到不同距离处的计算能量值，然后根据上文提出的修正方法，将Modtran计算结果和经验公式混合使用，得到所关注的能见度10 km情况下的修正透过率以及修正能量，理论计算结果与实验结果分别如表2和表3所示。

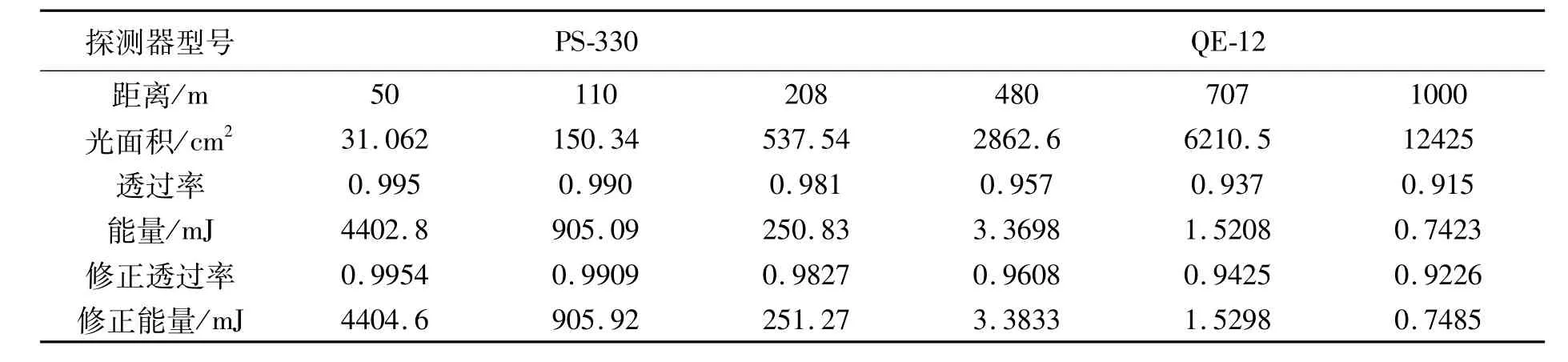
表2 理论计算结果Tab.2 Results of theorical calculation

表3 实验结果Tab.3 Results of experiments

在50 m处，能量抖动比为8.3％，而在1 km处，能量抖动比为50.2％。除了激光器本身输出能量抖动6.18％以外，其余均是在传输过程中大气湍流引起的抖动，即在50 m和1 km处分别为2.12％和44.02％。由此可见，在1 km处，能量抖动已经相当剧烈。

由表2和表3可知，理论计算的能量和实际测量的能量值符合并不是很好，但是几乎都在一个数量级，原因初步分析如下：（1）无论是软件还是经验公式的理论计算透过率和实际的天气变化情况存在一定差异；（2）在理论计算中，按照出口处光斑的形状进行相似扩大，即为中空矩形向远处传播，这与实际采集到的光斑图样存在差异；（3）激光在大气中的传播受到大气湍流影响，实际测量与理论计算允许存在偏差。图8、图9分别是300 m位置光斑烧蚀图和能量分布图。

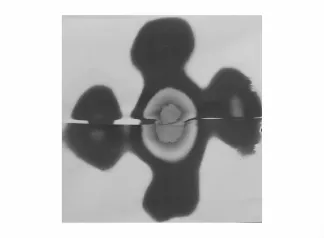
图8 CO2光斑烧蚀图

图9 CO2光斑能量分布

由图8和图9可知，经过激光器输出镜的衍射，光斑已经不再保持出口处的形状，而如此复杂的衍射光斑图样难以通过理论进行模拟，采用均匀能量分布近似造成了比较大的偏差。除掉以上影响因素之外，上文中所提出的透过率修正方案在一定程度上是有效的，也就是在所关注的10 km能见度下透过率比5 km时的透过率要高，这是符合常理的，至于差异的大小跟探测距离有关系，探测距离越远，二者差异越大，说明修正效果越明显，因此该修正方法对于长距离传输，更加有利。

由表3还可以看出，能量抖动比随着探测距离的增加而增加，而且在对应距离处与10月21日所做结果接近，将21日和22日实验测得的光束能量抖动比如图10所示。

图10 CO2光斑能量抖动比

由图10可知，2009年10月21日和22日测量结果变化趋势相同，其中还可以发现一个问题：21日所做实验中P1点出现一定的跳变，而这两个位置正好是采用不同型号的探测器；22日实验中，P2点也正好对应于能量抖动比变化剧烈的位置，而这也正是更换探测器的临界位置，所以上图中的两个跳变剧烈的点均可以认为是由不同的探测器接收面积和光谱响应所造成的。

5 结 论

本文在经典Mie散射理论基础上，分析了在雷达系统设计中需考虑的激光大气透过率的经验计算公式，指出了该经验公式的不足之处，分析了大气分析计算软件MODTRAN自身的优点，结合二种方法的优点对大气透过率进行了估计。在该理论指导下，进行了CO2激光大气传输实验，由于没有考虑大气湍流，理论计算和实验结果存在一定偏差，但不影响本文提出方法的实用性。实验测量得出激光器出口处光斑能量抖动比为6.18％，在50 m和1 km处分别为8.3％和50.2％，表明随着传输距离增加，能量抖动比逐渐增大。除掉出口处激光光斑本身的抖动之外，主要由大气传输引起的能量抖动在50 m和1 km处分别为2.12％和44.02％。实验结果显示，水平传输1 km时，能量抖动已经相当剧烈，所以对更远距离的传输，自适应光学补偿十分必要。

［1］阴俊燕，尹福昌，陈明，等.影响激光大气传输因素分析［J］.红外与激光工程，2008，37：399-402.

YIN JY，YIN F CH，CHEN M，et al..Impact on laser transmission in atmosphere［J］.Infrared and Laser Eng.，2008，37：399-402.（in Chinese）

［2］于继平，齐文宗，郭春凤，等.激光大气传输特性的数值模拟［J］.激光与红外，2008，38（6）：523-527.

YU JP，QIW Z，GUO CH F，et al..Numerical simulation of laser propagation through atmospheric turbulence［J］.Laser＆Infrared，2008，38（6）：523-527.（in Chinese）

［3］庞春颖，张涛.激光主动成像系统信噪比模型的研究［J］.光学精密工程，2008，16（2）：615-621.

PANG CH Y，ZHANG T.Signal-to-noise ratio model of laser active imaging system［J］.Opt.Precision Eng.，2008，16（2）：615-621.（in Chinese）

［4］MCDONALD T E.Range-gated imaging experiment s using gated intensifiers［J］.SPIE，1999，3642：142-148.

［5］DAVID D，STEVE B.Long-range laser illuminated imaging：analysis and experimental demonstrations［J］.Opt.Eng.，2001，40（6）：1001-1009.

［6］王智，贾书洪，张晓辉，等.激光主动成像图像的多帧后处理算法研究［J］.光学精密工程，2007，15（4）：615-621.

WANG ZH，JIA SH H，ZHANG X H，et al..Multiframe postprocessing algorithm of laser active imaging images［J］.Opt.Precision Eng.，2007，15（4）：615-621.（in English）

［7］COOKE C R.Automatic laser tracking and ranging system［J］.Appl.Opt.，1972，11（2）：277-284.

［8］袁纵横，张静，张文涛，等.基于大气湍流效应的双波长激光传输特性实验研究［J］.光学技术，2009，35（5）：686-690.

YUAN ZH，ZHANG J，ZHANGW T，etal..Experimental study on transmission characteristics of dualwavelength laser in atmospheric turbulence［J］.Opt.Technique，2009，35（5）：686-690.（in Chinese）

［9］柯熙政，马冬冬，刘佳妮.激光在雾中传输的衰减研究［J］.光散射学报，2009，21（2）：104-109.

KE X ZH，MA D D，LIU JN.Study attenuation of laser transmission in fog［J］.Chinese J.Light Scattering，2009，21（2）：104-109.（in Chinese）

［10］袁易君，任德明，胡孝勇.Mie理论递推计算散射相位函数［J］.光散射学报，2006，17（4）：366-371.

YUAN Y J，REN D M，HU X Y.Computing scattering phase function by recursive formula of Mie theory［J］.Chinese J.Light Scattering，2006，17（4）：366-371.（in Chinese）

［11］FU Q，SUNW B.Mie theory for lightscattering by a spherical particle in an absorbingmedium［J］.Appl.Opt.，2001，40（9）：1353-1361.

［12］WICOMBEW J.Improved Mie scattering algorithms［J］.Appl.Opt.，1980，19：1505-1509.

［13］戴永江.激光雷达原理［M］.北京：国防工业出版社，2001.

DAIY J.The Principle of Lidar［M］.Beijing：National Defence Industry Press，2001.（in Chinese）

［14］吴健，杨春平，刘建斌，等.大气中的光传输理论［M］.北京：北京邮电大学出版社，2006.

WU J，YANG CH P，LIU JB，et al..Optical Transmission Theory in the Atmosphere［M］.Beijing：Beijing University of Posts and Telecommunications Press，2006.（in Chinese）

郭 劲（1964—）：男，吉林长春人，研究员，博士生导师，主要从事光电对抗技术与装备研制等方面的研究。

E-mail：guojin_1964＠126.com

M easurement of CO2laser atmospheric transm ission property based on M ie scattering

ZHANG He-yong，WANG Ting-feng，SHAO Jun-feng，ZHAO Shuai，GUO Jin
（State Key Laboratory of Laser Interaction with Matter，Changchun Institute of Optics，Fine Mechanics and Physics，Chinese Academy of Sciences，Changchun 130033，China）

In order to calculate the atmospheric transmittance more correctly，the empirical expression of atmosphere transmittance which should be considered in the design of lidar systems based on Mie theory was analyzed in this paper，and the disadvantage of the empirical expression was demonstrated.In consideration of themerits both the empirical expression and MODTRAN software，they were combined to calculate the atmospheric transmittance.As a result，amodified transmittance expression was achieved.The atmospheric transmittance experiments of CO2laser were completed under the theory above.The actual results and the theory have some differenceswithout considering the atmosphere turbulence，but there is no impact on the practica-bility of the theory.The experimental results show that the energy drift ratio of the laser is 6.18％at the outputwindow，and 8.3％and 50.2％at the distances of50m and 1000 m，respectively，whichmeans the ratios increase with the enlargement of distance.Themain reason of the drift is the atmospheric transmission according to the experimental environments.Excluding the drift ratios at the outputwindow of the CO2laser，the energy drift ratios are 2.12％and 44.02％at50m and 1 000m，respectively.The experimental results demonstrate that the energy twitter has been so fiercely at1 000 m，therefore，the adaptive optics compensation is very important in the long-range atmospheric transmission.

atmosphere transmission；Mie scattering；MODTRAN software；CO2laser；energy drift ratio

TN249；P407.5

A

1674-2915（2010）04-0353-10

book=362,ebook=64

张合勇（1982—），男，贵州福泉人，硕士研究生，主要从事激光大气传输以及激光应用等方面的研究。

E-mail：yonghezhang1116＠126.com

王挺峰（1977—），男，山东文登人，博士研究生，副研究员，硕士生导师，主要从事激光应用等方面的研究。

E-mail：wtfeng＠sina.com

邵俊峰（1984—），男，安徽淮北人，硕士研究生，主要从事激光与物质相互作用等方面的研究。

E-mail：shao_junfeng＠hotmail.com

赵 帅（1981—），男，吉林通化人，硕士研究生，主要从事激光应用等方面的研究。

E-mail：zs040148＠yahoo.com.cn

2010-03-12；

2010-06-13

中国科学院院长优秀奖获得者科研专项启动资金