梁端位移对轻轨车辆运行的影响分析

刘志雄，徐彩彩，陈进杰

(1.石家庄铁道学院，石家庄 050043;2.西南交通大学 土木工程学院，成都 610031)

桥梁受荷载作用后将引起梁端位移，包括竖向位移和转角，这种位移的存在将对轨道结构产生影响。在传统的有砟轨道上，由于道砟的流动特性，这种微小的位移一般不会对轨道结构产生影响;但在无砟轨道上，由于轨道系统与桥梁处于较大的刚性连接状态，桥梁的微小变形都将对轨道系统产生影响［1］。

图1为梁端位移的不同形式对轨道结构的影响示意图。本文就梁端转角和错台两种梁端位移对行车速度比较低的轻轨车辆运行的影响进行计算和分析，评价列车运行的舒适性及安全性。

图1 不同形式梁端位移对轨道结构的影响示意

1 计算方法

1.1 计算模型

梁端位移导致轨道线形变化，使钢轨产生挠曲变形。为简化分析，车辆的横向振动忽略不计，对钢轨发生挠曲变形情况下的车辆垂向振动进行分析计算，以进一步评价其对车辆运行的影响。

当两股钢轨上的垂向不平顺相同或相近，即轨道上只存在线路中心线的高低不平顺时，车辆因左右两轨差异而激化的侧滚振动可以忽略，车辆垂向振动可取线路中心线所在立面为对称面对半个车辆进行建模型分析。半车模型如图2所示。车体考虑沉浮与点头两个位移，车体与转向架构架间为二系悬挂的弹簧刚度和阻尼。类似地，转向架构架也只考虑沉浮与点头两个位移，构架与车轮间是一系(或轴箱)弹簧刚度与阻尼，假定振动过程中车轮不脱离轨面运行，车轮的位移与轨面垂向不平顺相等，车轮没有振动自由度，由此，根据哈密尔顿原理建立半车6自由度的车辆振动方程。

1.2 车辆振动方程

由梁端位移所引起的轨面不平顺时程函数为ηV(t)，4个车轮下的轨面不平顺激励函数为ηVi(t)，(i=1～4)(编号自前进方向第1车轮开始)，由于4个车轮经过同样的轨面不平顺，所以4个车轮下的激励不是独立的，可以根据车轮经过同一轨面点上的时间差进行换算。设4个车轮经过同一轨面点的时间分别为 t1、t2、t3、t4，则有

图2 车辆垂向振动平面模型

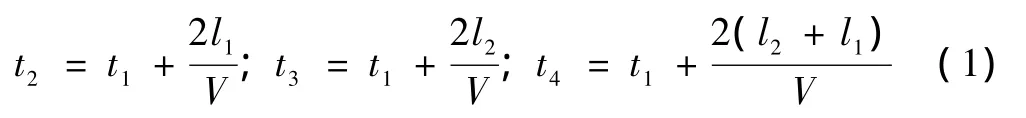
根据哈密尔顿原理，建立六自由度车辆振动方程

以上式中各参数含义介绍如下:

V——车速;

zc、ζc——车体的沉浮和点头振动位移;

zbi、ζbi——前后构架的沉浮和点头振动位移;

mc、Jcζ——分别表示一个车体的垂向参振质量和点头转动惯量;

mb、Jbζ——分别表示一个转向架构架的垂向参振质量和点头转动惯量;

c1、c2——分别表示一系(每轴箱)和二系(每转向架单侧)悬挂的阻尼;

k1、k2——分别表示一系(每轴箱)和二系(每转向架单侧)悬挂的刚度;

ηVi——4个车轮下轨面不平顺激励;

l1——转向架上前后两轮对一系悬挂纵向中心距之一半;

l2——车辆二系悬挂纵向中心距之一半。

1.3 计算参数

采用上述六自由度模型，运用有限元法进行分析，车体和转向架构架分别简化为质量单元，考虑沉浮和点头转动惯量。一系和二系悬挂弹簧采用弹簧阻尼单元模拟，计入刚度和阻尼。计算中所需各参数数值见表1。

表1 轻轨车辆垂向振动计算参数表

本文舒适度评判标准采用欧洲规范“EUROCODE”对客车车体垂向振动加速度的评定标准见表2。

表2 “EUROCODE”客车车体垂向振动加速度评定标准

2 梁端位移对车辆运行影响的分析结果

2.1 梁端转角对车辆运行的影响

仅考虑主桥侧发生较大梁端转角、而另一侧桥台或引桥梁端转角为0，车辆运行方向考虑两个方向，分别为车辆由有转角侧向无转角侧运行，以及由无转角侧向有转角侧运行两种情况，轻轨车辆在桥上的运行速度取30 km/h，分析由于梁端转角引起钢轨局部线型的变化对车体的竖向位移、速度和加速度的影响，特别是对车体振动加速度的影响，见图3。

图3 线路挠曲示意

2.1.1 车辆由无转角侧驶入转角侧

以梁缝处扣件间距为780 mm为例，不同梁端转角情况下车体动力响应的最大值如表3所示。

由表3可知:①随着桥梁转角的增大，车体的垂向位移、速度和加速度变化幅度均增大，基本呈线性关系。不同转角下的车体垂向位移、速度和加速度时变情况如图4所示。②桥梁一侧发生正的转角和负的转角时，只影响车体垂向动力响应的方向，而不改变其幅度和大小。③由于车辆从无转角侧进入有转角侧，车体垂向位移随线路状态而发散。④在最大转角4.2‰情况下，车体垂向振动加速度最大值达0.004 g，可认为对车辆乘坐舒适性无影响，在实际发生的更小转角情况下，可忽略其对车辆运行平稳性的影响。

表3 不同梁端转角下车辆动力响应最大值

图4 由无转角侧驶入转角处时不同转角下车体垂向位移、速度和加速度时程曲线

2.1.2 车辆由有转角侧驶入无转角侧

由于上述分析中桥梁一侧发生正的转角和负的转角时，只影响车体垂向动力响应的方向，而不改变其幅度和大小，所以以下只取转角为正的情况进行分析。不同梁端转角情况下车体动力响应的最大值如表4所示。

表4 不同梁端转角下车辆动力响应最大值

由表4可知:①当车辆由转角侧驶入无转角侧时，比车辆由无转角侧驶入有转角侧的车体动力响应大，在梁缝处扣件间距一定的情况下，随着桥梁转角的增大，车体的垂向位移、速度和加速度变化幅度均增大，基本上呈线性关系。不同转角下的车体垂向速度和加速度时变情况如图5所示。②无其它不平顺干扰情况下，车辆从有转角侧驶入无转角侧时，车体垂向位移是收敛的，且随着时间的变化逐渐趋于零。③在最大转角4.2‰情况下，车体垂向振动加速度最大值达0.094 g，可认为对车辆乘坐舒适性无影响，在实际发生的更小转角情况下，可忽略其对车辆运行平稳性的影响。

2.2 错台对车辆运行的影响

由于桥梁支座的弹性作用，在列车荷载作用下，有荷载一跨桥梁发生弹性变形，另一侧没有变形，这样就容易在梁缝处产生错台。此外，支座失效、施工误差等因素都有可能引起错台，从而影响车辆的运行［3］。桥梁错台后的轨道结构形式如图1，错台后的线路挠曲情况如图6(以错台1 mm为例)。

由于梁缝处扣件间距不同，由桥梁错台引起的线路变形基本相等，因此，本文仅以扣件间距780 mm为例进行分析。桥梁不同错台高度下的车体垂向位移、速度、加速度随时间的变化如图7所示。

图5 由有转角侧驶入无转角侧时不同转角下车体垂向速度、加速度时程曲线

图6 错台后钢轨挠曲示意

研究表明:①随着错台高度的增加，车体垂向位移、速度和加速度值变大，具体数值见表5。②错台高度为3 mm时，车体竖向振动加速度为0.006 5 g，量值较小，对行车舒适性无影响。对于实际中错台比较小的情况，可不考虑其对轻轨车辆运行的影响。

表5 错台对车体运行的影响

图7 错台后车体垂向位移、速度、加速度时程曲线

3 结论

桥梁受荷载作用后将引起梁端竖向位移和转角，使轨道产生竖向不平顺，对系统产生影响，从而影响行车舒适性及安全性。通过对桥梁转角及错台对轻轨车梁的运行舒适性及安全性分析，得出如下结论:

1)桥梁一侧发生正的转角和负的转角时，只影响车体垂向动力响应的方向，而不改变其幅度和大小。

2)随着桥梁转角的增大，车体的垂向位移、速度和加速度变化幅度均增大，基本呈线性关系。

3)车辆从桥梁有转角一侧驶入无转角侧，比从无转角一侧驶入有转角一侧的动力响应强烈，但转角达到4.2‰时，车体最大垂向加速度为0.094 g，可认为对车辆乘坐舒适性无影响，在实际发生的更小转角情况下，可忽略其对车辆运行平稳性的影响。

4)随着错台高度的增加，车体垂向位移、速度和加速度值变大，但量值较小，对行车舒适性无影响。

［1］申磊.梁端无砟轨道扣件受力系统分析［D］.成都:西南交通大学，2008.

［2］张珍珍.250 km/h客运专线弹性支撑块式轨道结构参数研究［D］.成都:西南交通大学，2009.

［3］刘学毅.车辆—轨道—路基系统动力学［M］.成都:西南交通大学，2009:20-23.