凸显优势

顾燕红

(深圳大学数学与计算科学学院，广东 深圳 518060）

0 引言

本文把注意力集中在闭区间上连续函数极值与凸函数的关系上。学生如能学习到这些内容，将对他们以后掌握运筹学相关内容有不少帮助，这样的处理在许多微积分教科书及参考书上(如[1]－[5])都还没有出现。

1 问题

定义 1：把[a ,b]上连续函数在(a ,b)内仅有一个最小点 x0的函数记为M(x)，并且若M(x)满足条件：(A)在[a,x0) 上单调递减，在(x0,b]上单调递增，则称此函数为单谷函数，记为S(x)，如图1所示。

能够看出M(x) 是一种相对容易求得最小点的函数类。事实上，在运筹学的规划理论与算法研究中， 一个重要的思想就是把一些性质不太好的函数经过巧妙的变换，使之成为有类似于或比M(x) 有更良好特性的函数，然后再来求解最小值。

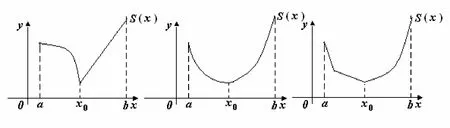
图1 单谷函数S(x)Fig.1 Unique valley function S(x)

现在的问题是，如果一个 M(x)不是 S(x)，那么它会出现怎样的情况呢？我们将用一个实例来说明这样一个现象：存在非 S(x)的 M(x)，其在 x0点的任何邻域内都不会单调(小于x0时单减，大于x0时单增)。此现象指出如果没有条件(A)， M(x)可能无法成为一个“单谷”。那么有没有较好的判别(A)是否成立的法则呢？

2 分析

首先来看一个函数，记为E(x)。此函数定义在[−1,1]上，这里仅描述它的[−1,0]部分，而(0,1]这一部分与[−1,0)部分关于坐标纵轴对称(如图2所示)。

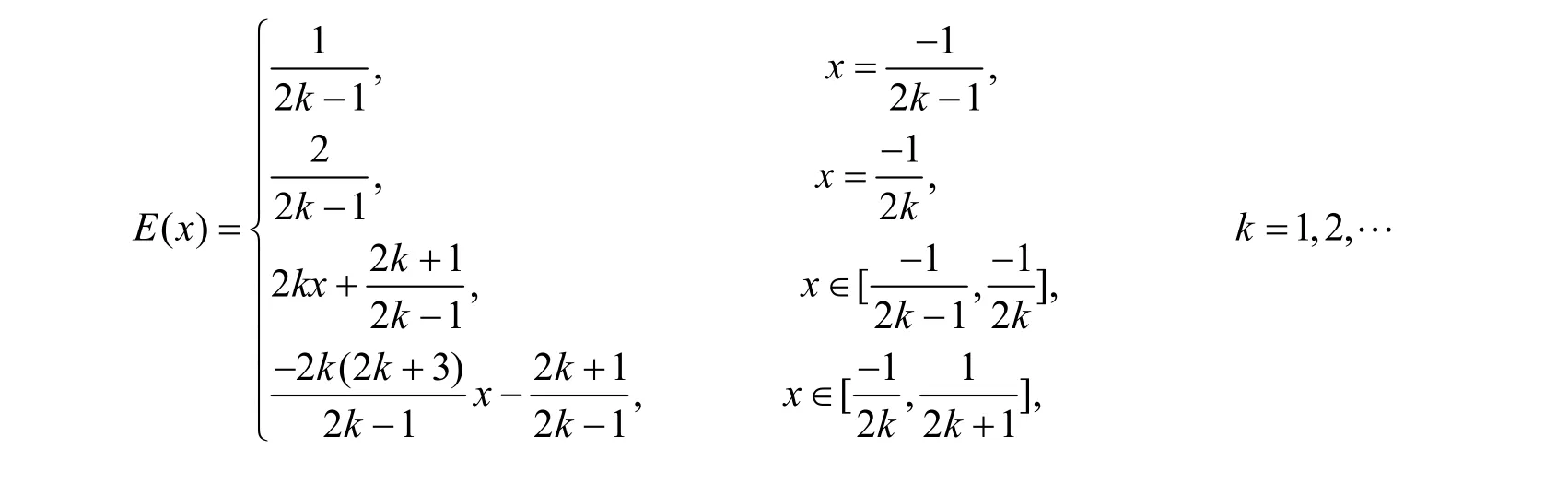
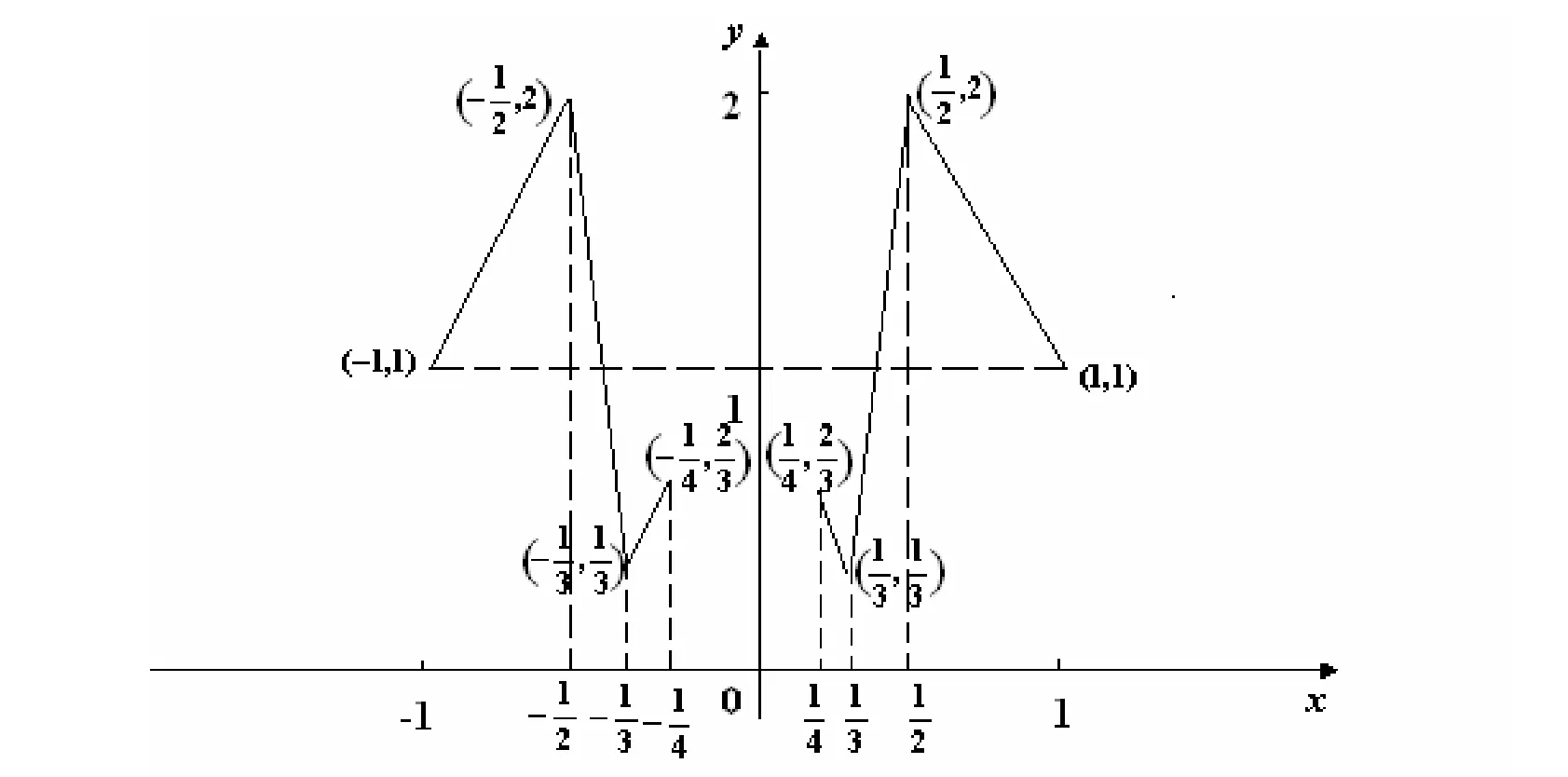
图2 函数E(x)的图形Fig.2 Figure of function E(x)

很明显，E(x)在[1,1]−上连续，且当00x=时，达到唯一最小值0。同时此函数在0点的任何邻域内都不是单调的，所以它是一个M(x)，但不是单谷函数S(x)。那么S(x)定义中的条件(A)何时会成立呢?下面是一个重要的判别准则。

性质：M(x)是S(x)的一个充分条件是M(x)为凸函数。

有趣的是，如果M(x)的定义中要求是在[a ,b]上一阶连续可导，则上述性质仍成立，并且也就可以构造出类似于E(x)的例子(这是一道很好的习题)。另外，还可以和学生讨论凸函数是否是连续的、可导的这些较难的问题，让他们意识到函数极值与凸性之间的密切关系，这对学生以后学习运筹学的重要分支非线性规划是很有好处的。

3 结论

通过上节内容的论述，我们把凸函数性质在微积分学中强调了一下。鉴于对函数凸性的应用在设计求各类非线性函数极值的算法中的重要性[6-7]，这种新的处理对学生今后学习优化理论与算法是很有实际意义的。

[1]同济大学数学教研室.高等数学.4版[M].北京:高等教育出版社, 1996.

[2]赵树嫄.经济应用数学基础(一) 微积分[M].北京:中国人民大学出版社, 1988.

[3]韩云瑞.高等数学典型题精讲[M].大连:大连理工大学出版社, 2001.

[4]陈传璋, 金福临, 朱学炎, 等.数学分析[M].北京:高等教育出版社, 1983.

[5]斐礼文.数学分析中的典型问题与方法[M].北京:高等教育出版社, 1993.

[6]DIMITRI P B , ANGELIA N, ASUMAN E O.Convex Analysis and Optimization[M].Belmont, Mass:Athena Scientific, 2003.

[7]DIMITRI P B.Nonlinear Programming[M].Belmont, Mass:Athena Scientific, 1999.