一类修正Navier-Stokes方程解衰减速率的上下界估计

吴珞

一类修正Navier-Stokes方程解衰减速率的上下界估计

吴珞

（上海第二工业大学理学院，上海 201209）

Navier-Stokes方程描述了具有小速度梯度的不可压缩粘性流体运动规律，在流体动力学研究中有着重要的应用。1966年，Ladyzhenskaya O. A. 放弃了速度梯度很小的限制，提出了几种描述不可压缩粘性流体运动规律的修正Navier-Stokes方程。为估计整个三维空间上一类修正Navier-Stokes方程解衰减速率的上下界，使用改进的Fourier分解方法得到当初值模衰减速率上界为；对某些初值时，解的模衰减速率下界为(t+1)−34。

修正Navier-Stokes；大时间行为；衰减率；上界；下界

0 引言

文献[1]和[2]独立研究了不可压缩粘性流体运动规律，提出了描述速度梯度较小的流体运动规律的经典Navier-Stokes方程。1966年，文献[3]和[4]放弃了流体速度梯度较小的限制，给出了几种修正Navier-Stokes方程，其中之一形式如下

的修正Navier-Stokes方程问题。当初值满足一定条件，n≤3时，该问题存在整体唯一解[5-8]。

文献[9]首先提出了经典Navier-Stokes方程解的衰减估计问题。文献[10]讨论了小初值解的衰减估计问题。1985年和1986年，文献[11-13]利用Fourier分解方法给出整个空间经典Navier-Stokes方程解的衰减估计，证明当初始值u∈L2∩Lq(1≤q ＜2)时，解的L2模，并且给出了解的衰减下界估计。1991年，文献[14]讨论了带权空间上解的衰减下界估计。之后，有一系列这方面的研究成果出现，例如文献[15-23]。

有关修正Navier-Stokes方程解的衰减估计问题研究不多。文献[24,25]使用Fourier分解方法研究了文献[3]和[4]提出的另一类修正Navier-Stokes方程解的衰减估计问题，其方程为

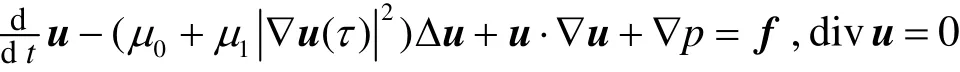
其中∇u(τ)为∇u(τ)的L2模。本文将使用Fourier分解方法研究三维空间上一类修正Navier-Stokes方程(1)～(4)解的衰减估计，将证明当初值（1≤p＜2）时，问题(1)～(4)解的L2模，对某些初值。

本文的第1节将回顾记号、定义和结论。在第2节，我们将讨论修正Navier-Stokes方程问题解的衰减上界。在第3节，我们将给出解的衰减下界估计。

在本文中，我们假设n=3且f=0。为了书写方便，取μ0=1，μ1=1。

1 记号、定义和结论

2 解的衰减上界估计

为证明上述定理，我们给出以下两个引理：

引理2.2[12]设，1≤p＜2，r( t)＞0，则

引理2.3设u是问题(1)～(4)的解，则

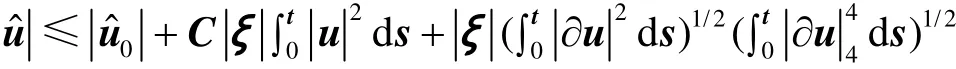
证明在(1)两边做Fourier变换得到

证毕。

证明定理2.1由(1)和(2)知

3 解的衰减下界估计

为了估计修正Navier-Stokes方程问题(1)～(4)解的衰减下界，我们记w=u−v=u−，则

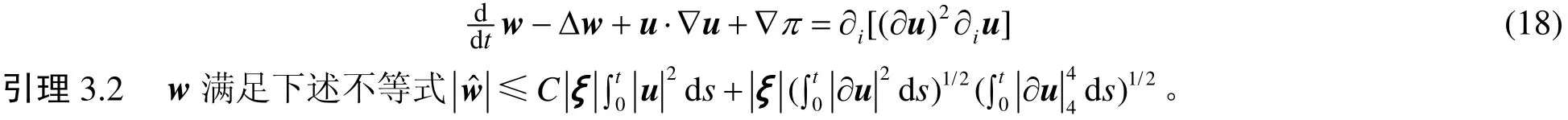
证明证明与引理2.3相似。

成立。

证明定理3.1由(18)，使用(5)和(6)知

与证明(15)相似，我们可证：对任取r( t)＞0，

为估计(20)，我们回顾文献[13]中的一个不等式

在(20)中应用引理3.2，定理3.1，(7)和(21)，我们可推出

4 结论

当外力f=0时，三维空间上一类修正Navier-Stokes方程解衰减速率有上下界。当初值(1≤p＜2)时，解的L2模的衰减速率上界为；对某些初值)时，解的L2模的衰减速率下界为。当外力随时间无限增大时有一定衰减速率，应用本文方法易知修正Navier-Stokes方程解有相同的上下界。

[1] NAVIER C L M H. On the laws of motion of fluids taking into consideration the adhesion of the molecules[J]. Ann.Chim.Phys. ,1822,19:234-245.

[2] STOKES G H. On the theories of the internal friction of fluids in motion[J]. Trans.Cambridge Phil.Soc. ,1845,8:287-319.

[3] LADYZHENSKAYA O A.On certain nonlinear problems of the theory of continuous media[C] // s. n. . Internat.Congress of Mathematicians. Moscow:s. n. ,1966:149.

[4] LADYZHENSKAYA O A.The Mathematical Theory of Viscous Incompressible Flow[M]. New York: Gordon and Breach,1969.

[5] LADYZHENSKAYA O A.On new equations for the description of the motion of viscous incompressible fluids, and the global solvability of their boundary value problems[J]. Trudy Mat.Inst.Akad.Nauk SSSR,1967, 102:85-104.

[6] LADYZHENSKAYA O A.On modifications of the Navier-Stokes equations for large gradients of velocities[J]. Zap.Nauchn.Sem.Leningr.Otd. Mat.Inst. , 1968, 7:126-154.

[7] LADYZHENSKAYA O A. The Mathematical Problems of the Dynamics of a Viscous Incompressible Fluid (in Russian)[M]. Moscow: Nauka, 1970. [8] LIONS J L.Quelques Méthodes de Résolution des Problèmes aux Limites Non Linéaires[M]. Paris: Gauthier Villars, 1969.

[9] LERAY J. Essai sur le mouvement d'un liquide visqueux emplissant l'espace[J]. Acta Math. , 1934, 63:193-248.

[10] KATO T. Strong Lpsolutions of the Navier-Stokes equations with applications to weak solutions[J].Math.Zeit. , 1984, 187:471-480.

[11] SCHONBEK M E.L2decay of weak solutions of the Navier-Stokes equations[J]. Arch.Rational Mech.Anal. , 1985, 88, 209-222.

[12] SCHONBEK M E. Large time behaviour of solutions to the Navier-Stockes equations[J]. Comm.Partial Differential Equations, 1986, 11(7):733-763.

[13] KAJIKIYA R,MIYAKAWA T. On L2decay of weak solutions of Navier-Stokes equations inRn[J]. Math.Z. , 1986, 192:135-148.

[14] SCHONBEK M E. Lower bounds of rates of decay for solutions of the Navier-Stockes equations[J]. J.Amer.Math.Soc. , 1991, 4:423-449.

[15] ZHANG L. Sharp rate of decay of solutions to 2-dimensional Navier-Stokes equation[J]. Comm.Partial Differential Equations, 1995, 20:119-127. [16] CARPIO A. Large time behavior of incompressible Navier-Stokes equations[J]. SIAM J.Math.Anal. , 1996, 27:449-475.

[17] OGAWA T. Energy decay for a weak solution of the Navier-Stokes equation with slowly varying external forces[J]. J.Funct.Anal. , 1997, 144:325-358.

[18] CHEN Z M,MIYAKAWA T.Decay properties of weak solutions to a perturbed Navier-Stokes systems in Rn[J]. Adv.Math.Sci.Appl. , 1997, 7:741-770.

[19] TAKAHASHI S. A weighed equation approach to decay rate estimates for the Navier-Stokes Equations[J].Nonlinear Anal. , 1999, 37:751-789.

[20] OLIVER M. Remark on the rate of decay of higher order derivatives for solutions to the Navier-Stokes equations in Rn[J]. J.Funct.Anal. , 2000, 172:1-18.

[21] HE C,XIN Z P. On the decay properties of solutions to the nonstationary Navier-Stokes equations in R3[J]. Proc.Royal.Soc.Edinb: Sect A, 2001, 131:597-619.

[22] BAEA H O, JIN B J. Upper and lower bounds of temporal and spatial decays for the Navier-Stokes equations[J]. J.Differential Equations, 2005, 209:365-391.

[23] KUKAVICA I. Weighted bounds for the velocity and the vorticity for the Navier-Stokes equations[J].Nonlinearity, 2006, 19:293-303.

[24] 董柏青, 李用声. 一类修正的Navier-Stokes方程的长时间性态[J]. 数学物理学报, 2006, 26(A)(4):498-505.

[25] DONG B Q, JIANG W. On the decay of higher order derivatives of solutions to Ladyzhenskaya modelfor incompressible viscous flows[J]. Science in China, Series A: Mathematics, 2008, 51:925-934.

[26] TEMAM R. Navier-Stokes equations,theory and numerical analysis[M]. New York: North-Holland Amsterdam, 1977.

Upper and Lower Bounds of Decay Rates for a Solution of a Modified Navier-Stokes Equations

WULuo
（School of Science,Shanghai Second Polytechnic University,Shanghai 201209,P.R.China）

The Navier-Stokes equations have many important application in fluid dynamic,which describe motion characteristics of viscous incompressible fluids for small gradients of the velocities．In 1966,Ladyzhenskaya O．A．suggested several variants of modified Navier-Stokes equations to a determinate description of the nonstationary flows of viscous incompressible fluids for large gradients of the velocities．Forestimating upper and lower bounds of decay rates for a modified Navier-Stokes equations in the whole three-dimensional space,by improving the Fourier splitting methods，the paper proves that upper bounds of decay rates of L2norm to the solution arefor initial value(1≤p＜2) and lower bounds of ones arefor some initial value

modified Navier-Stokes equations；large time behavior；decay rate；upper bounds；lower bounds

O175.2

A

1001-4543(2010)03-0173-05

2010-06-03;

2010-06-29

吴珞(1963—)，男，辽宁辽阳人，教授，博士，主要研究领域为应用数学，电子邮件：wuluo@sspu.cn

上海市自然科学基金(No.09ZR1412800)；上海市教育委员会科研创新项目基金(No.10ZZ131)