GPS高程拟合方法在风场测量中的应用①

孟现彪,史雅茹,冯 禹,闫 利

(1.武汉大学测绘学院,湖北武汉43007;2.内蒙古电力勘测设计院,内蒙古呼和浩特010020)

0 引 言

如何把大地高转化为正常高,成为GPS高程应用的一个重要问题。解决高程转换问题的方法主要有两个:一是综合利用GPS测量资料和高程异常资料确定点的高程;二是综合利用GPS测量资料和水准测量资料确定似大地水准面的高程。

由GPS测得点的大地高 H是以椭球面(WGS-84)起算的,但在实际应用中,地面点的高程常采用正(常)高高程系统。其正常高(H正常)是以似大地水准面起算的,叫大地水准面差距[3,4]。

地面上一点A的大地高HAg与正常高H正常的关系为[2]

其中:ξ为高程异常,表示参考椭球面与似大地水准面之间的高程差。

经过GPS网的三维平差,可获得各点的大地高HAg,如果在其中一些点上同时进行水准测量(即已知该点的正常高 Hr),则该点的高程异常可按(2)式求出。

在一局部GPS网中,由若干个点的 HAg值作为已知值,用数值拟合方法内插出其它GPS测点的高程异常,按式(l)可求得各点的正常高。若测区内测量点的数量足够多,且分布较为均匀,则可拟合测区的似大地水准面形状,进而推算测区中其余未进行水准联测的GPS点的高程异常值得出正常高,这种方法可称为“几何法”GPS高程拟合法。高程拟合计算的方法有:加权均值法、多项式曲线拟合、多项式曲面拟合、多面函数曲面拟合、线性移动拟合法、神经网络法等[1-6],其中多项式曲面拟合法应用最广。

1 GPS高程拟合方法

1.1 多项式曲面拟合法

设GPS基线向量网经二维约束平差后,求得各点的空间直角坐标 xi、yi和大地高平差值Hi,已知网中有n个点(网中总点数为m)具有正常高Hri。则可确定这些点的高程异常ξi为[1,2]

设点的高程异常ξi与坐标(x,y)之间函数关系如下:

其中:f(x,y)为ξ中趋势值,ε为模型误差。

根据n个GPS点的ξi可以确定多项式(4)中的系数。当n≥6时,可拟合确定所有系数,当n≥3且n＜6时,可拟合确定a0、a1、a2三个系数;当n＜3时只能确定a0一个系数。所以这种方法应至少具有3个已知高程点。对于每个已知点,在最小二乘准则条件下,解出各ai,当已知高程点分布均匀且测区内地形平坦时,这种方法拟合确定的高程异常i精度可望达到10～20 cm,甚至优于5 cm。在确定了多项式(4)中的系数后,即可应用该式求定其余测站点的高程异常值。数据操作流程如图1所示[2]。

图1 系统数据流程图

1.2 多面函数拟合法

多面函数法的基本思想是:任何数学表面和不规则的圆滑表面,总可用一系列有规则的数学表面的总和以任意精度逼近[1,2]。

设GPS测点ξ和x、y存在如下函数关系

式中:ai为待定系数,Q(x,y,xi,yi)是x和y的二次核函数,ξi可由二次式的和确定,故称多面函数。常用的简单核函数,一般采用具有对称性的距离型,即

式中:d=(x-xi)2+(y-yi)2,δ称为平滑因子,用来对核函数进行调整;b一般可选某个非零实数,常用或式(6)可写成误差方程的矩阵形式

待定系数a可根据已知点上的已知高程异常值,按最小二乘法计算

由上式求出多面函数的待定系数,就可按(5)式计算各GPS点的高程异常值。多面函数拟合法拟合高程异常,核函数Q和光滑因子δ的选择对拟合效果有非常重要的影响,对于每个区域都应该认真研究和选取,如果核函数Q和光滑因子δ选取合适,其拟合精度与二次曲面拟合相当。

2 精度评定

为了能客观地评定GPS水准计算的精度,在布设几何水准联测点时,应适当多联测几个点,其点位也应均匀地布设全网,以作外部检核用。

2.1 内符合精度[3、4]

根据参与拟合计算已知点的高程异常ξi与拟合高程异常ξi′,求出拟合残差Vi=ξi′-ξi,然后按下式可计算出GPS水准拟合计算的内符合精度(设参与拟合的已知点共有n个):

2.2 外符合精度[1,2]

根据检核点的高程异常ξi与拟合高程异常ξi′,求出拟合残差Vi=ξi′-ξi,然后按式(9)可计算出GPS水准拟合计算的外符合精度值(设检核点共有n个)。各高程拟合模型的内符合精度都较高且不同拟合模型的内符合精度相差不大,所以在后面的实践中取外符合精度作为评价各拟合方法好坏的标准,称之为拟合中误差,记作μ。

2.3 精度评定

1)根据检核点至已知点的距离L:km或测站数n,按表1计算检核点拟合残差来评定GPS水准所能达到的精度;

2)用GPS水准求出的GPS点间的正常高高差,在已知点间组成附合或闭合高程导线,按计算的闭合差W与表1中允许残差比较,来衡量GPS水准所能达到的精度。

表1 几何水准允许的限差

3 实例分析

3.1 测区概况

内蒙古兴安盟科右前旗风电场49.3 MW风电特许权项目,位于内蒙古自治区兴安盟科右前旗境内,测区至阿荣旗省际大通道从测区西北角穿过,交通便利。测图面积为30 km2,测区地形大部分为丘陵地形,地形低洼处大部分为耕地,地势起伏变化较大。测区平均海拔高差大约400 m左右。

3.2 测量仪器及软件

1)仪器:GPS接收机(天宝5700GPS);水准仪(莱佧NA728型水准仪);计算机。

2)软件:天宝后处理软件《T rimble Geomatics Office GPS后处理软件》(V1.62);清华三维平差软件《工程测量控制网微机平差系统》。

3.3 野外测量和数据处理

在测区内布设17个E级GPS控制点,并对8个点进行水准测量,构成闭合线路,经检验其精度达到了四等水准的精度,然后在各点上进行GPS观测,并与两个国家三角点联测,采用边角联式进行联网测量,其点位分布及网形如图2所示。

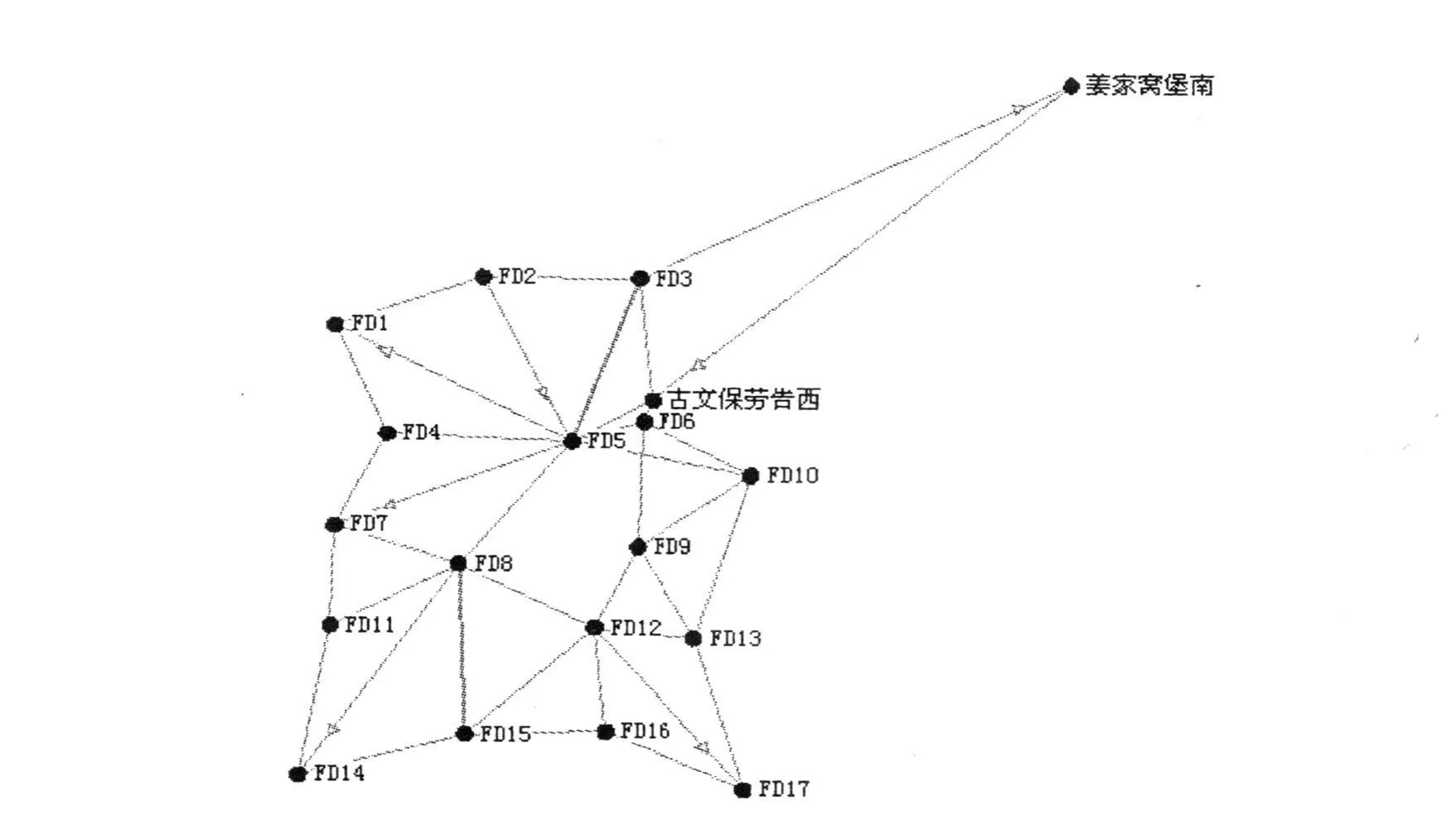
图2 GPS点位分布及网形图

野外获取数据后,经室内清华三维平差软件、天宝后处理软件TG0(V1.62)平差和基线处理后得到各观测点的平面坐标、大地高和正常高见表2。

表2 二维约束平差后GPS点的BJ54坐标、大地高及高程异常

点名 X/(m) Y/(m) 大地高/(m) 正常高/(m) 高程异常/(m)FD1 5127993.873 21441733.041 378.701 382.988 -4.287 FD2 5128461.890 21443096.210 411.933 416.249 -4.316 FD3 5128438.183 21444537.142 448.390 452.736 -4.346 FD4 5126903.989 21442207.926 420.569 424.863 -4.294 FD5 5126814.883 21443909.367 434.349 438.679 -4.330 FD6 5127001.679 21444569.864 437.763 442.108 -4.345 FD7 5125994.214 21441724.489 397.420 401.703 -4.283 FD8 5125603.691 21442857.633 390.609 394.916 -4.307 FD9 5125760.357 21444506.538 410.104 414.446 -4.342 FD10 5126464.032 21445557.705 398.636 403.001 -4.365 FD11 5125000.154 21441683.617 386.710 390.991 -4.281 FD12 5124962.826 21444109.139 399.840 404.172 -4.332 FD13 5124850.668 21445028.807 413.187 417.539 -4.352 FD14 5123506.423 21441381.049 361.684 365.956 -4.272 FD15 5123903.260 21442915.421 361.692 365.998 -4.306 FD16 5123914.025 21444202.580 416.273 420.606 -4.333 FD17 5123330.984 21445469.443 403.186 407.545 -4.359

平面拟合选取11种不同已知点的组合方案进行实验,按公式(9)计算不同方案的GPS高程拟合中误差(以下简称为中误差)。

表3 不同水准点布设方案的平面拟合结果/mm

从表3可以看出:由方案1、4、9、10的拟合结果可知,在本测区采用平面拟合的方法时,已知点数越多拟合中误差越小,但当已知点个数达到一定数目时(本测区为6),增加已知点的个数不能显著提高拟合精度;由方案1、2、4、6、7、8的拟合结果可知,已知点的分布对拟合精度的影响巨大(不同点位分布的拟合精度最大相差了5、6倍),当已知点均匀分布于整个测区时,拟合精度最高,分布在测区一端时精度最差;由此可知平面拟合不宜外推,所以应选取均匀分布于整个测区的点进行水准联测。此外,方案2、5、6、8、9、10的拟合中误差均小于4 cm,所以采用平面拟合法对本测区进行高程拟合,只要已知点个数大于3个,点位分布均匀,都能取得较好的拟合结果,这是测区面积小、高差小、高程异常变化平缓的缘故。

3.4 GPS水准方法的综合运用

对于测区面积不大且地势起伏较小的区域,拟合时可以把整个测区视为一个连续的似大地水准面,选用一个拟合模型进行拟合。但是如果测区面积较大或地形起伏较大,似大地水准面的形状很复杂,这样把该测区视为一个整体进行拟合,存在很多局限且精度很低。为此,可进行分区拟合,以提高拟合精度。分区拟合的首要任务是把测区分成几个小测区。小测区划分方法常用的有两种:一是根据测区的实际地形起伏情况划分,如把平原地区、丘陵地区和山区分别分为拟合小测区进行拟合。该方法简捷易行,常被采用。二是根据支撑点的高程异常来划分,首先用一种拟合方法求出支撑点的高程异常,然后比较相邻点的高程异常的差值,其差值在一定范围内的区域划分为拟合小测区。这种方法精度高,但工作量大,实际拟合时常灵活运用这两种方法[5]。

4 结 论

GPS水准拟合高程的精度与己知点数量、分布位置及拟合方法有关[6]。当己知点均匀分布于整个测区时,其点数越多,GPS水准高程拟合的精度越高,但当己知点数达到一定数量(本测区为6)时再增加己知点数,不能显著地提高待定点的精度,因为在这种情况下影响拟合模型精度的主要因素是似大地水准面的不规则程度和粗糙程度。当己知点均匀分布于整个测区时,拟合精度最高。在此讨论的多项式曲面拟合法在测区地形起伏不大的地区可以达到优于四等水准的精度。

在面积较大或者地形复杂的GPS测区,单独采取一种模型进行高程异常拟合,模型的拟合中误差很大,拟合结果不理想,难以满足测量工程的精度要求。而采用所提出的将整个测区划分为几个小区,分区进行拟合,可以获得令人满意的结果和精度,在实际测量工作中非常适用并且是可行的。

[1] 杨江波,李为乐,余代俊,陈哲锋.GPS高程拟合方法的实验研究[J].测绘科学,2009,34(3):54-57.

[2] 高 伟,李振洪,吴云孙.GPS高程拟合系统的研究[J].武汉测绘科技大学学报,1999,24(4):336-339.

[3] 徐绍铨,张华海,杨志强,等.GPS测量原理及应用[M].武汉:武汉大学出版社,2003.

[4] 张 勤,李家权.全球定位系统(GPS)测量原理及其数据处理基础[M].西安:西安地图出版社,2001.

[5] 于小平,杨国东,等.GPS高程拟合转换正常高的研究[J].测绘科学,2007,32(2):40-53.

[6] 康世英.GPS测量高程异常拟合方法探讨[J].地矿测绘,2007,23(2):5-8.