基于ARIMA模型的地球自转变化预报

李英冰

(武汉大学测绘学院,湖北 武汉 420079)

0 引 言

地球自转运动表征着地球的整体运动状况,以及地核、地幔、地壳、海洋和大气等各圈层之间的相互作用过程[7]。地球自转运动主要包括两部分:一是地球自转速率的变化,用周日变化(UT1-UTC)表征[1-7]。图1是1992年1月1日至2008年7月30日UT1-UTC的时间序列图,数据采样率为1天,该数据从地球自转服务(IERS)处下载。二是地球瞬时自转轴相对于地球表面的运动,简称为极移(PM)[8-10],PM的主要激发因素是地球上物质分布的变化[1,8]。图2是PM 的时间序列图,图中虚线是x分量,实线为y分量。

图1 UT1-UTC的时间序列

图2 极移分量的时间序列

地球自转变化的预报具有重要的科学意义和实用价值:

1)地球自转参数是精密大地测量必不可少的基本数据,如GMAIT、BERNESE、GIPSY 等精密解算软件必须实时更新准确的地球自转变化数据。

2)用于月球、火星等星球探测的空间飞行器的正常运行需要准确的地球自转变化数据。在航天器导航和跟踪中,地球自转变化的不确定性是主要的误差源。如果地球自转参数不准确,有可能导致卫星飞行器不能准确入轨。

近几十年来,随着甚长基线干涉、人卫激光测距和全球定位系统等现代测地技术的飞速发展,极大地推动了地球自转运动的研究。美国海军天文台的McCarthy和美国喷气推进实验室的Gross等专家长期专注于地球自转变化的预报研究[3,5]。常用方法有最小二乘法、协方差法、神经网络法、自回归移动平均法、小波分析、卡尔曼滤波等方法[2-5,9],预报准确度已经达到较高水平。

1 大气与海洋变化对地球自转变化的影响

全球流体变化会对地球自转变化产生影响[1]。自转运动与大气和海洋活动的研究受到广泛关注,1995年,IUGG/IAG专门设立了大气和海洋与地球自转相互作用的专题研究组。1998年,IERS组建了全球地球物理流体中心(GGFC),其下辖有大气、海洋等7个分中心,各分中心定期公布最新的观测数据和模型研究成果[1,10]。

对大气角动量(AAM)和海洋角动量(OAM)进行积分运算,能够分别计算出大气和海洋变化对地球自转变化的贡献。其中AAM数据可以从美国国家环境预报中心(NCEP)获取,OAM数据可从GGFC下载,数据采样率都为6 h。

通过对AAM 和OAM的chi3分量积分,可得大气和海洋变化对UT1-UTC的贡献,积分结果表示为UTAAM+UTOAM。通过对AAM和OAM的轴分量积分,可得大气和海洋变化对PM的贡献,表示为PMAAM+PMOAM。积分公式为

图3是UTAAM+UTOAM的时间序列,时间区间为2001年1月1日至2008年7月30日。图4是PMAAM+PMOAM的时间序列,实线是x分量,虚线为y分量。

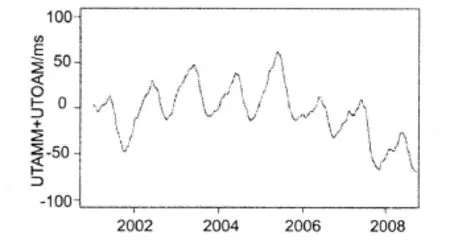
图3 UTAAM+UTOAM/(ms)

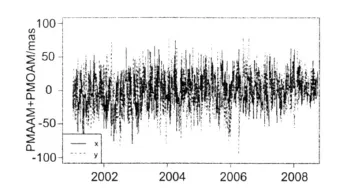
图4 PMAAM+PMOAM/(mas)

2 周日变化的预报

周日变化的预报算法如图5所示,主要包括建立预测模型和外推预测两个部分。预测模型建立的步骤包括减去周跳、潮汐、UT2-UT1、趋势项和周期项等。外推预测主要包括基于周日残差序列应用ARIMA进行外推预报,加上周期项、趋势项、UT2-UT1、潮汐、周跳等预测值。

建立预测模型主要步骤为

1)数据准备,从www.iers.org下载Finals.all(IAU2000)文件,抽取 UT1-UTC数据列,如图1所示。

2)UT1-UTC是不连续的,存在跳秒问题。因而需要移除跳秒,产生连续的UT1-TAI数据列。

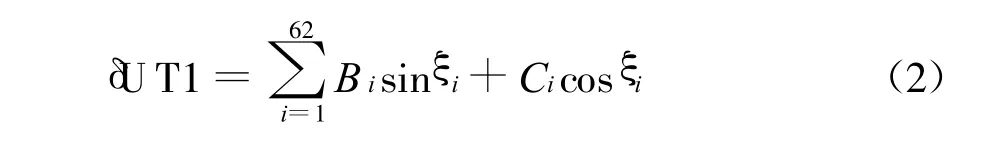
式中 :详见文献[6],进行潮汐改正后的结果记为UT1R-TAI。

(4)减去UT2-UT1,其中UT2-UT1的计算公式为

计算结果记为UT2R-TAI。以上数据的时间序列如图6所示。

(5)用最小二乘法计算趋势项和周期项,公式为

式中 :A0、A1、A2是趋势项的拟合系数,B0、B1、B2为周期项的拟合系数,φ1、φ2、φ3 为初始相位,ω1、ω2、ω3为周期项的频率,分别对应于半年、一年和Chandler周期项。移除趋势项和周期项后的数据序列记为 ΔΔ(UT2R-TAI)。

(6)利用AAM和OAM数据计算大气和海洋 变化对周日变化的贡献。

图5 UT1-UTC的预报算法

周日变化的外推预报过程包括

1)基于差分自回归移动平均模型(ARIMA)对序列(UT2R-TAI)进行外推预报。公式为

式中:X(t)=a1Xt-1+…+apXt-p+et+b1et-1+…+bqet-q,a1,……,ap是P阶自回归系统,b1,……,bq为q阶移动平均系数,d为差分阶数。当UTAAM和UTOAM参与计算时,需要采用多元回归模型(MAR)。

2)根据周期项的拟合系数,外推周期项的预报序列,并与 ΔΔ(UT2R-TAI)的预报值相加,得到残差和周期项Δ(UT2R-TAI)的预报值。

3)根据多项式的拟合系数,外推趋势项,将它与前面的预报结果相加,得到UT2R-TAI的预测值。

4)由公式(3)计算UT2-UT1的外推估值,并与前面的预测值求和,得到UT1R-TAI的预测值。

5)加上由公式(2)得到的潮汐预测估值,得到UT1-TAI的预测值。

6)加上跳秒,得到UT1-UTC的预测值。

利用上述算法进行实际计算,预测未来365天的UT1-UTC的数值。共进行实际预报720组,将预测值与实测值比较,统计预测误差绝对值的平均值(MAE),计算公式为

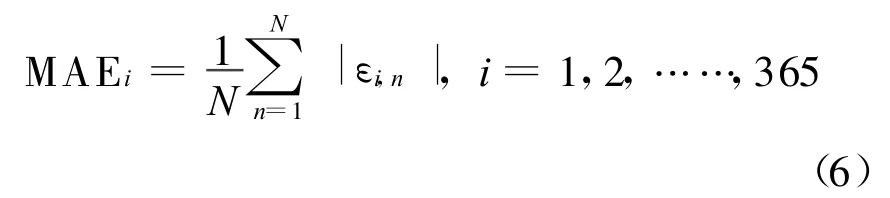
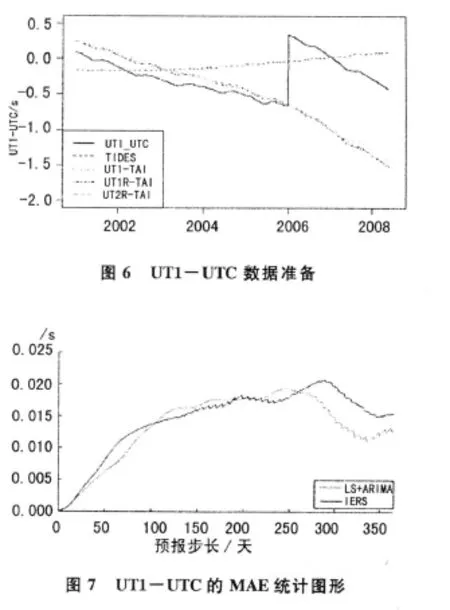
式中:εi,n是预报误差。图7中的虚线是周日变化的MAE统计曲线,实线是对IERS官方预报序列的MAE统计。我们的预报效果总体优于IERS成果,特别是近期预报。

3 极移变化的预报

极移变化的预报算法如图8所示,包括建立预测模型和外推预测两个部分。

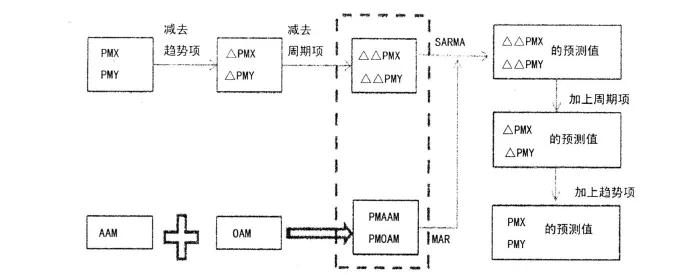
图8 极移的预报算法

在建立预测建模时,用最小二乘法计算出趋势项和周期项的拟合系数,计算公式为

上式中的符号含义与公式(4)一样。对残差序列的预报采用季节性自回归移动平均(SARMA)模型进行预报,公式为

式中S为季节项,其他参数含义与公式(5)相似。

图9 极移变化X分量的MAE统计图形

利用上述算法进行实际计算,预报未来365天的极移变化。进行实际预报720组,将预测值与实测值比较,并统计出MAE序列。图9和图10分别给出了极移X和Y分量的MAE统计曲线及其与IERS成果的对比。统计结果表明:一周内的超短期预报优于IERS成果,但整体结果要比IERS的成果略差。

图10 极移变化X分量的MAE统计图形

4 结 论

采用最小二乘法和ARIMA模型对周日变化进行预测,总体的预报效果要优于IERS发布的产品。采用最小二乘法和SARMA对极移变化进行预报,总体预报效果没有IERS的预报效果好。当采用AAM和OAM数据时,对于周日预报有轻微改善,但对极移的预报没有得到改善。

致谢:感谢美国俄亥俄州立大学的郭俊义和C.K.Shum教授提供的访美经费支持。

[1]Chao B F,Dehant V,Gross R S,and et al.Space geodesy monitors mass transports in global geophysical fluids[J].Eos Trans.,2000,81(22):247,249-250.

[2]Dickman S R.Determination of oceanic dynamic barometer corrections to atmospheric excitation of Earth rotation[J].J.Geophys.Res.,1998,103(B7):15127-15144.

[3]Gross R S,Eubanks T M,Steppe J A,and et al.AKalman-filter-based approach to combining independent Earth-orientation series[J].J.Geodesy,1998,72(4):215-235.

[4]Li Y B,Guo J Y,Shum C K,Johnson T.Empirical predictions of UT1 and polar motion using least squares fit and ARIMA[C]//AGU full meeting,San Francisco,2008.

[5]McCarthy,Luzum.Prediction of Earth Oriention[J].Bull Geod.,1991,65(1):18-22.

[6]McCarthy,D D,Petit G,IERS Conventions[R].Paris:Observatoire de Paris,2003.

[7]郑大伟,虞南华.地球自转及其和地球物理现象的联系:I日长变化[J].地球物理学进展,1996,11(2):81-101.

[8]虞南华,郑大伟.地球自转及其和地球物理现象的联系:II地极运动[J].地球物理学进展,1996,11(3):71-81.

[9]王琪洁.基于神经网络技术的地球自转变化预报[D].中国科学院研究生院博士学位论文,2007.

[10]周永宏,郑大伟,虞南华,廖新浩.地球自转运动与大气、海洋活动[J].科学通报,2000,45(24):2258-2597.