北斗二代/SINS组合导航系统研究①

戴邵武,马长里,代海霞

(1.海军航空工程学院,山东 烟台264001;2.北京清华同方工业有限公司,北京10083)

0 引 言

我国正在运行的北斗一代卫星导航系统只是个初级区域导航定位系统。因此,我国的第二代卫星导航系统——北斗二代卫星导航系统已经立项并进入组网高峰期,预计在2015年形成覆盖全球的卫星导航定位系统。正在建设的“北斗二代”卫星导航系统将由5颗静止轨道卫星(GEO)和30颗非静止轨道(中轨(MEO)及倾斜地球同步圆轨道(IGSO))卫星组成[1]。虽然北斗二代卫星定位系统可达到很高的定位精度,但在特殊时刻和特殊地区由于信号受到遮挡容易出现丢星现象,而惯性导航则不受时间和地点的限制,可自主导航。如何使北斗二代和捷联惯导进行组合,使之更好地完成导航定位任务,是当前我国在该领域研究的热点问题[2]。

1 北斗二代定位原理

“北斗二代”卫星导航系统的基本工作原理是[3]:空间段卫星接收地面控制系统上行注入的导航电文及参数,并连续向地面用户发播卫星导航信号,用户收到至少四颗卫星信号后,进行伪距测量和定位解算,最后得到定位结果。同时,为了保持地面控制系统各站之间的时间同步,以及地面站和卫星之间时间同步,通过站间和星地时间比对,完成地面站间和卫星与地面站间的时间同步。分布在国土内的监控站负责对可视范围内的卫星进行监测,采集各类观测数据后将其发送至主控站,由主控站完成卫星轨道精密确定及其它导航参数的确定、广域差分信息和完好性信息处理,形成上行注入的导航电文参数。

2 北斗二代/SINS伪距、伪距率组合模型的建立

对北斗二代/SINS组合导航系统的设计采取伪距、伪距率的组合模式。在组合之前要进行选星,以得到视野内最佳的卫星几何构型。受篇幅所限,不对选星算法做具体研究,可参考文献[4]。该组合模式中,接收机只提供星历数据和伪距、伪距率即可,省去导航计算处理部分,有精度高、鲁棒性好、抗干扰强的特点。组合导航原理图如图1所示。

图1 伪距、伪距率组合导航系统原理图

2.1 北斗二代/SINS状态模型

捷联惯导的误差方程表示为[5]

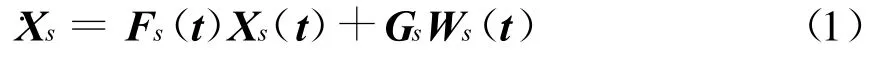
系统的状态向量定义为

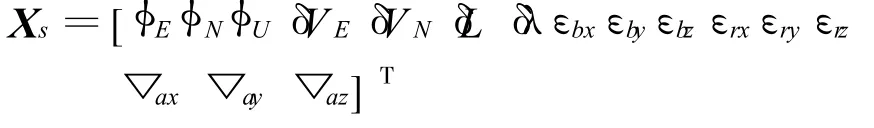
式中:下标E、N分别代表东向和北向;L为载体所处的纬度,λ为载体所处的经度;φE、φN、φU代表东 、北、天方向的姿态误差角;εbxεbyεbz代表东 、北、天方向的等效陀螺漂移,▽ax▽ay▽az代表东、北、天方向的等效加速度计漂移。

BeidouII的状态向量同样取为时钟误差相应的距离和时钟频率误差相应的距离率,分别设为δ tu2和 δ tru2,其微分方程为

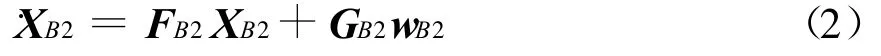
所以BeidouII/SINS组合系统的状态向量为

组合导航的状态模型为

式中:

2.2 北斗二代/SINS量测模型

1)伪距量测方程

由SINS载体到卫星Sj的伪距为ρIj,可表示为[6]

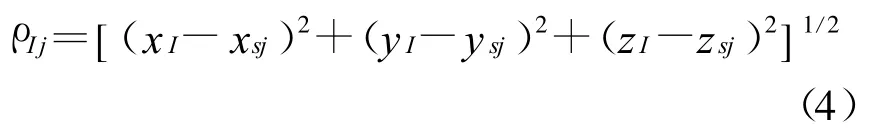
设SINS位置的坐标为[x,y,z]T,将(4)式在[x,y,z]T处展开成泰勒级数,取一次项:

令:

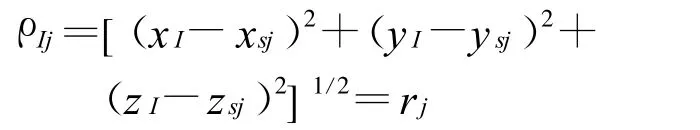
同时接收机测得的伪距为

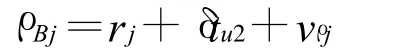
则伪距量测值可以写成

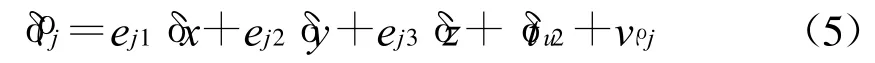
取j=1,2,3,4得

又由(x,y,z)与空间直角坐标系的变换关系式:

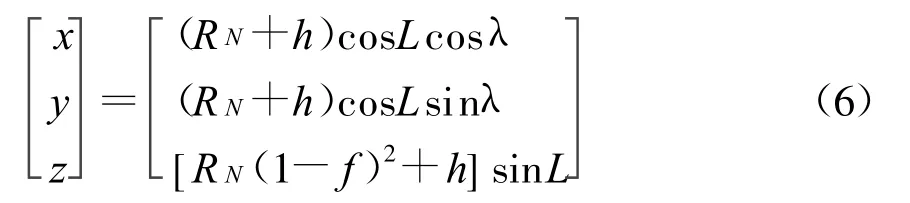
可得伪距量测方程

式中:

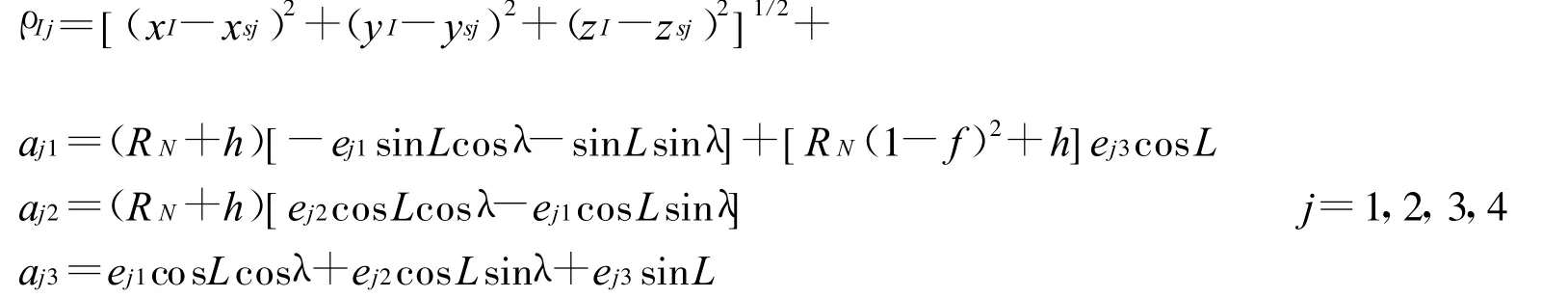
2)伪距率量测方程

对应于捷联惯导给出的位置处的伪距率为

接收机测得的伪距率为

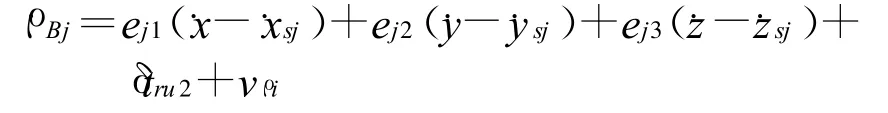
则伪距率量测方程如下:

取j=1,2,3,4得

式中:δ﹒x、δ﹒y、δ﹒z为地球直角坐标系中表示的速度误差,可通过变换坐标系将 δ﹒x、δ﹒y、δ﹒z表示为[7]

则可获得伪距率量测方程

式中:

式中:

将伪距量测方程和伪距率量测方程合并成组合导航的量测方程为:

3 组合导航系统仿真

整个组合导航系统的仿真总体结构主要包括初始参数设置、飞行器轨迹仿真、惯导输出仿真、BeidouII系统的仿真、选星及卡尔曼滤波算法。仿真整体结构图如图2所示:

对于运动的载体,由于导航系统是时变的,系统矩阵和量测矩阵的确定都与载体的位置、速度有关,因而在仿真前,要对飞行轨迹进行设计,以提供仿真量测值。本文为了全面研究飞行载体各种机动飞行对仿真性能的影响,设计一个比较完整且机动飞行较多的飞行轨迹(包括平飞、转弯、爬升和加速等飞行状态),仿真时间共1400 s。

图2 组合导航系统仿真流程图

平台初始误差角取为东向100′,北向100′,天向200′;三维速度、位置误差分别为1 m/s,50 m,陀螺漂移为0.1(°)/h,等效加速度计零偏为10-4g,陀螺相关时间为0.1(°)/h,陀螺白噪声漂移为0.1(°)/h。飞机初始位置为北纬32°,东经118°,高度2000 m。初始航向0°,速度350 m/s。伪距测量的误差涉及到卫星时钟误差(由卫星星历获得)、卫星星历误差、电离层和对流层延迟误差、多路径效应误差和接收机有关的误差等,上述误差经过改正及补偿后可大大降低伪距测量的误差。假设伪距测量噪声是标准差为20 m的白噪声。对上述飞行轨迹进行仿真分析,仿真后的航迹轨迹、平台误差角、速度误差和位置误差分别如图3～6所示:

图3 航迹轨迹

仿真误差稳态值如表1所示,结果表明,基于伪距、伪距率的SINS/BeidouII组合导航系统可有效提高导航精度。为我国北斗二代和捷联惯导组合导航的研制、开发提供了思路。

表1 基于伪距、伪距率组合导航系统的稳态误差值

4 结 论

仿真结果表明,该组合算法可得到很高的导航精度,对环境的变化也有较强的适应性,有利于工程应用,为北斗二代卫星和捷联惯导的组合提供了思路。

[1] 石 华.中国北斗二代覆盖全球[N].环球时报,2007-03-25(3).

[2] 乔 洋,赵育善,赵金才.惯性导航/双星组合导航的可行性研究[J].上海航天,2003,(4):34-37

[3] 随 艺.北斗卫星和伪卫星组合定位系统研究[D].西北工业大学,西安:2004

[4] 袁建平,罗建军等.卫星导航原理与应用[M].北京:中国宇航出版社,2004.

[5] 林雪原,刘建业,范胜林.三星定位/SINS伪距组合导航系统的研究[J].中国空间科学技术,2002,(6):6-11.

[6] 林雪原,何 友.双星定位/捷联惯导组合导航技术[J].上海交通大学学报,2005,39(9):1485-1488.

[7] 张友安,林雪原,徐胜红.综合导航与制导系统[M].北京:海潮出版社,2005,306-307.