济宁矿区BJ-54至WGS-84坐标转换模型改进及精度分析①

刘永义,党亚民,郑作亚,3

(1.中国测绘科学研究院大地测量与地球动力学研究所,北京100830;2.山东科技大学测绘科学与工程学院,山东青岛266510;3.海岛(礁)测绘技术国家测绘局重点实验室,山东 青岛266510)

0 引 言

随着GPS导航定位技术的日臻完善,GPS测量技术也逐渐满足了全球范围、全天候、连续实时以及三维导航和定位服务的要求,并具有常规测量系统无法比拟的优点。GPS测量所采用的坐标系统是WGS-84坐标系,WGS坐标系是质心坐标系统[1],其原点位于地球的质心上,实际应用中需要转化为国家大地坐标系或者地方坐标系。常用的三维坐标转换模型有布尔莎模型、Molodensky模型、武测模型[2]等。这些转换模型都为七参数模型,即3个坐标平移参数,3个旋转角参数和1个尺度比参数。

我国自2008年7月1日开始启用2000国家大地坐标系,国家测绘局在公告中提供了新坐标系的技术参数。公告同时对新旧坐标系的转换和使用做出了说明:2000国家大地坐标系与现行国家大地坐标系转换、衔接的过渡期为 8～10年。现有各类测绘成果,在过渡期内可沿用现行国家大地坐标系;2008年7月1日后新生产的各类测绘成果应采用 2000国家大地坐标系。现有地理信息系统,在过渡期内应逐步转换到2000国家大地坐标系;2008年7月1日后新建设的地理信息系统应采用2000国家大地坐标系。

因此,坐标转换就显得尤为重要,但布尔萨模型适用于全球范围的坐标转换,且为了提高所求得参数的精度和稳定性,要求公共点均匀分布。而在实际应用中局部地区GPS控制网的范围往往只有数十到数百平方千米,甚至更小。例如济宁二号井,测区面积只有90 km2。这样控制点的范围就比较近,此时旋转参数和平移参数的相关性很大,参数的精度和稳定性会出现坐标转换的病态性问题[3],即微小的测量误差或点位移动就会导致转换参数值有很大误差。

文献[4]中提出的站心坐标转换改进模型,能有效地削弱方程的病态问题,并可提高转换参数精度。本文引用此改进模型,并对引文中验证方法稍作改进,把引文中引进的1 cm误差改为1 mm,更能说明布尔萨模型在此工程中进行改进的必要性,而且引入了高程坐标误差,对其进行检验。因为GPS高程定位的精度相对于平面定位的精度本身就要低一些。但结果表明,高程中产生的误差同样对所得七参数结果也有很大影响。通过实测数据利用fortran编程[5],将布尔萨模型与改进模型求得的转换参数进行了比较,验证了站心坐标转换改进模型比布尔萨模型更适用于小区域的坐标转换。

1 布尔萨模型

布尔萨模型共采用了7个参数,分别是3个平移参数X0、Y0、Z0,3个旋转参数 εX、εY、εZ(又称为3个欧拉角)和一个尺度比参数m。布尔萨七参数公式[4]如下

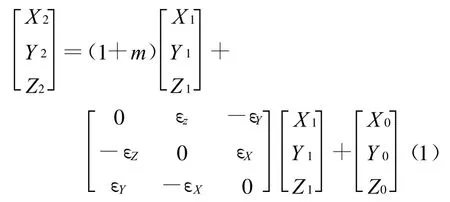
式中:X1、Y1、Z1是测站在已知坐标系中的坐标,X2、Y2、Z2是测站在待求坐标系中的坐标。

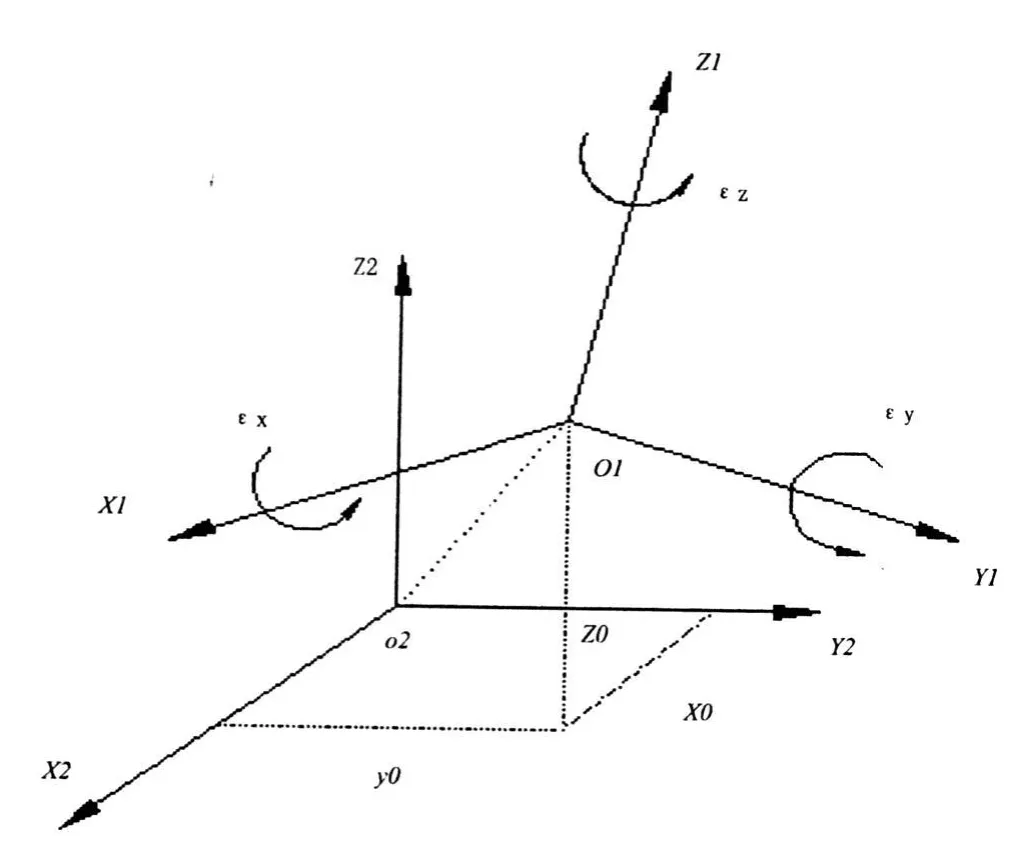
图1 两个空间直角坐标系之间的关系[6]

2 坐标转换改进模型

坐标转换改进模型主要采用站心坐标系,可以有效降低坐标转换时平移参数之间的相关性,减少法方程矩阵的病态性。首先进行坐标系转换,此处的坐标系转换是指球心空间直角坐标系与站心直角坐标系之间的转换,即将球心空间直角坐标系转换为站心直角坐标系。

将公共点在WGS-84地心坐标系中的坐标以及在BJ-54坐标系中的坐标都分别转换成相对于各自虚拟坐标原点(定义为点的平均坐标点)的站心坐标。

GPS坐标(XG,YG,ZG)转换为站心坐标(XG 1,YG1,ZG1),首先求出各公共点的GPS平均坐标(¯XG,¯YG,¯ZG)作为其站心坐标的虚拟坐标原点,然后各点坐标分别减去其平均坐标,即将GPS坐标转换为站心坐标(XG 1,YG1,ZG1),写成公式为

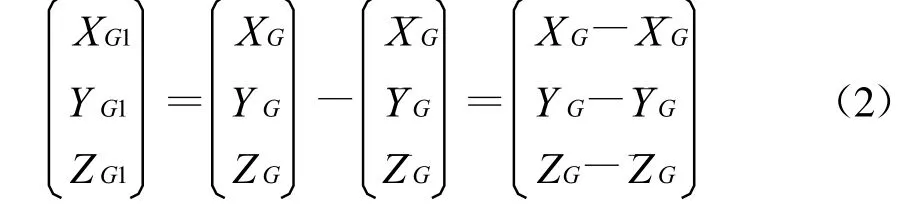
地方坐标(XT,YT,ZT)转换为站心坐标(XT1,YT1,ZT1),首先求出各公共点的地方坐标系平均坐标(¯XT,¯YT,¯ZT)作为其站心坐标的虚拟参考点,然后各点坐标分别减去该平均坐标便将地方坐标转换为站心坐标(XT1,YT1,ZT1),写成公式为

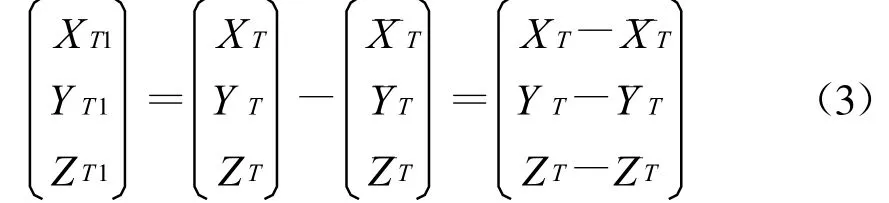
然后再经过坐标轴旋转,坐标轴平移,尺度统一,最后得到的GPS坐标转换的改进模型为

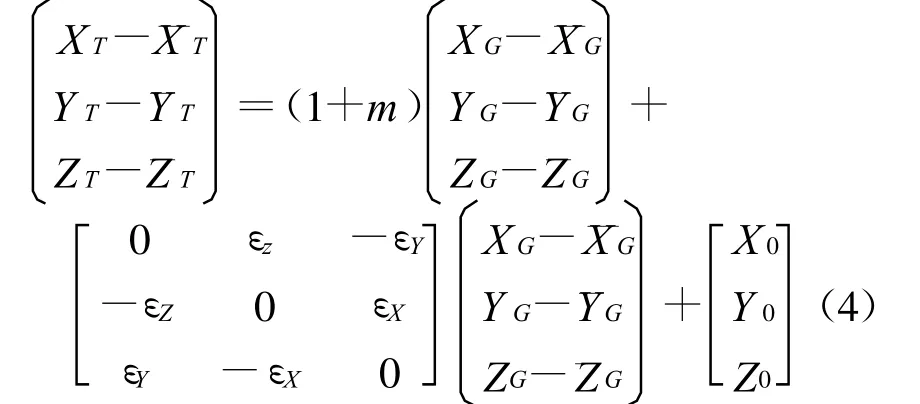
通过上式用3个或3个以上具有两套坐标值的公共点便可解得转换参数,然后利用求得的转换参数进行点的坐标转换,不过在转换后要注意:将转换后的坐标加上相对应的虚拟原点的坐标值才能得到相应的地心坐标或参心坐标[3]。

3 实测数据计算及分析

所用数据为济宁二号煤矿两套坐标系实测数据,测区面积90 km2,属于局部区域,满足本文开始所描述可能出现病态方程的情况。由于所验证的是:当原始数据出现微小误差时所求七参数的稳定性。因此验证方法如下:对测区内所取点的其中一个点的三维坐标分别做微小改动,实验中采用的是将点的X,Y,Z坐标分别改动0.001 m,其余坐标均不变,然后再用改动后点的坐标再次进行转换参数的求解,分别采用布尔萨模型和改进模型进行实验,比较两个模型中每个点变动后所求解的转换参数相对于初始值的变化情况,以检验其病态性。使用fortran语言,已知点为9个,实验分析结果如表1、2所示:

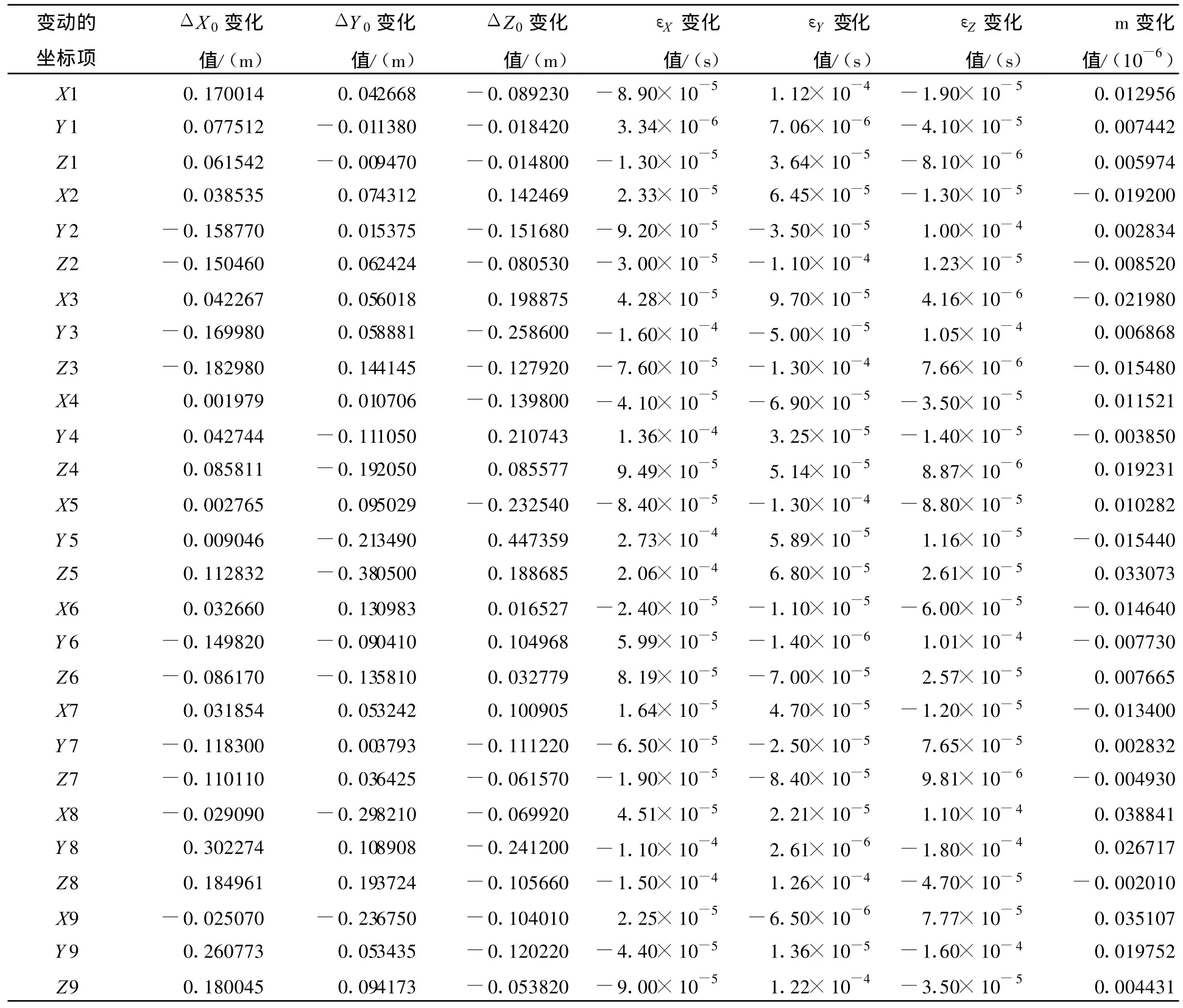
表1 布尔萨模型七参数变化值的检验

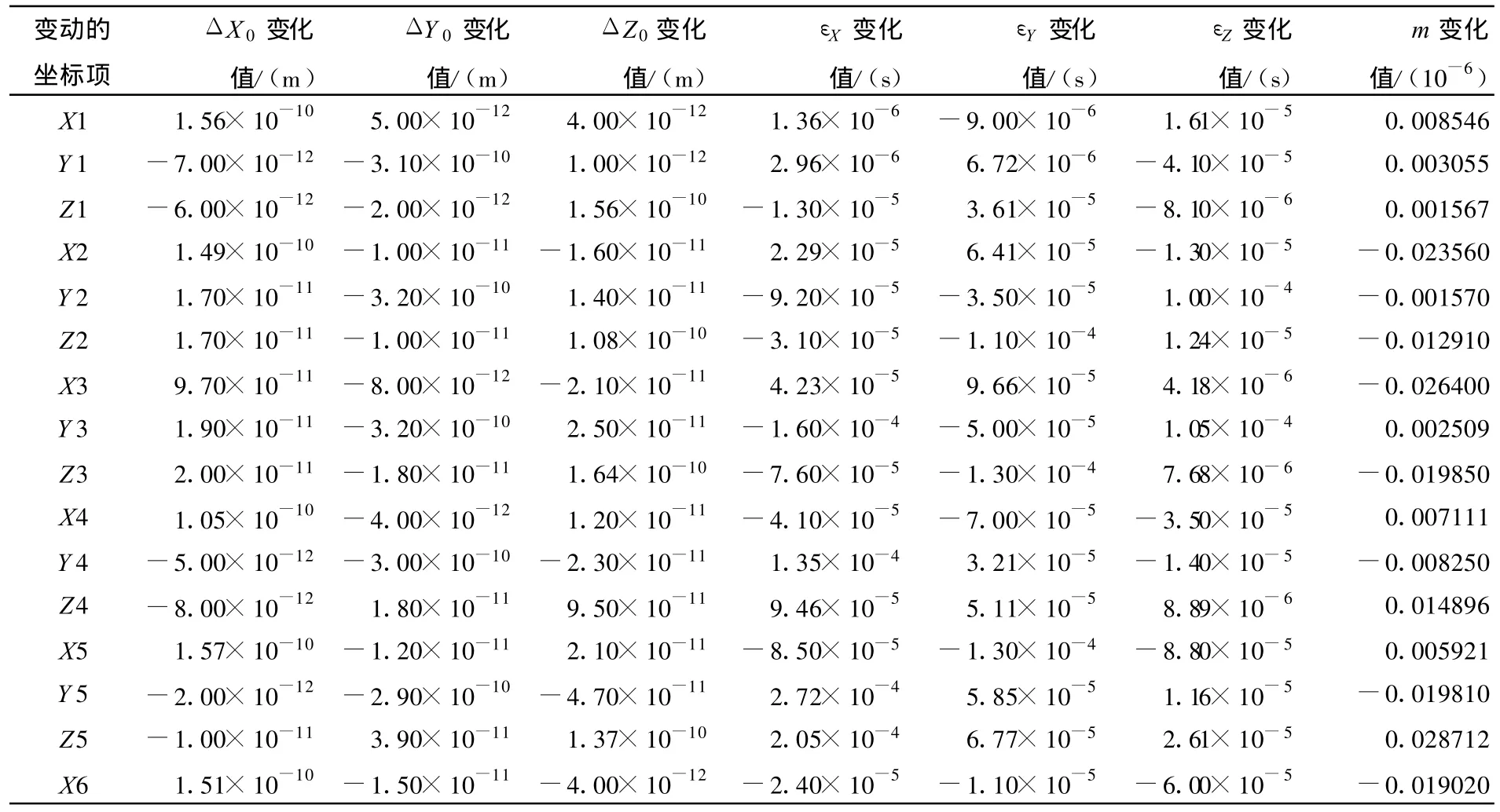
表2 改进模型七参数变化值的检验

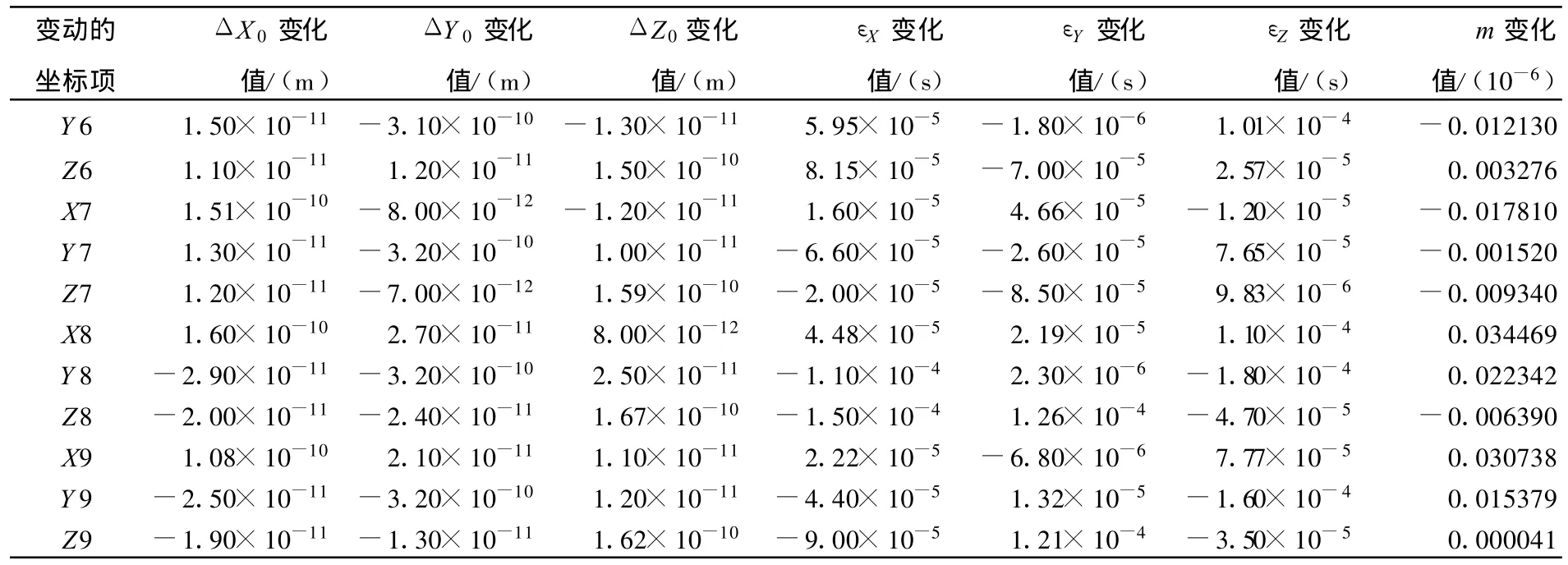
变动的坐标项ΔX0变化值/(m)ΔY0变化值/(m)ΔZ0变化值/(m)εX变化值/(s)εY变化值/(s)εZ变化值/(s)m变化值/(10-6)Y 6 1.50×10-11 -3.10×10-10 -1.30×10-11 5.95×10-5 -1.80×10-6 1.01×10-4 -0.012130 Z6 1.10×10-11 1.20×10-11 1.50×10-10 8.15×10-5 -7.00×10-5 2.57×10-5 0.003276 X7 1.51×10-10 -8.00×10-12 -1.20×10-11 1.60×10-5 4.66×10-5 -1.20×10-5 -0.017810 Y 7 1.30×10-11 -3.20×10-10 1.00×10-11 -6.60×10-5 -2.60×10-5 7.65×10-5 -0.001520 Z7 1.20×10-11 -7.00×10-12 1.59×10-10 -2.00×10-5 -8.50×10-5 9.83×10-6 -0.009340 X8 1.60×10-10 2.70×10-11 8.00×10-12 4.48×10-5 2.19×10-5 1.10×10-4 0.034469 Y 8 -2.90×10-11 -3.20×10-10 2.50×10-11 -1.10×10-4 2.30×10-6 -1.80×10-4 0.022342 Z8 -2.00×10-11 -2.40×10-11 1.67×10-10 -1.50×10-4 1.26×10-4 -4.70×10-5 -0.006390 X9 1.08×10-10 2.10×10-11 1.10×10-11 2.22×10-5 -6.80×10-6 7.77×10-5 0.030738 Y 9 -2.50×10-11 -3.20×10-10 1.20×10-11 -4.40×10-5 1.32×10-5 -1.60×10-4 0.015379 Z9 -1.90×10-11 -1.30×10-11 1.62×10-10 -9.00×10-5 1.21×10-4 -3.50×10-5 0.000041

以下为布尔萨模型和改进模型七参数变化值的比较图:

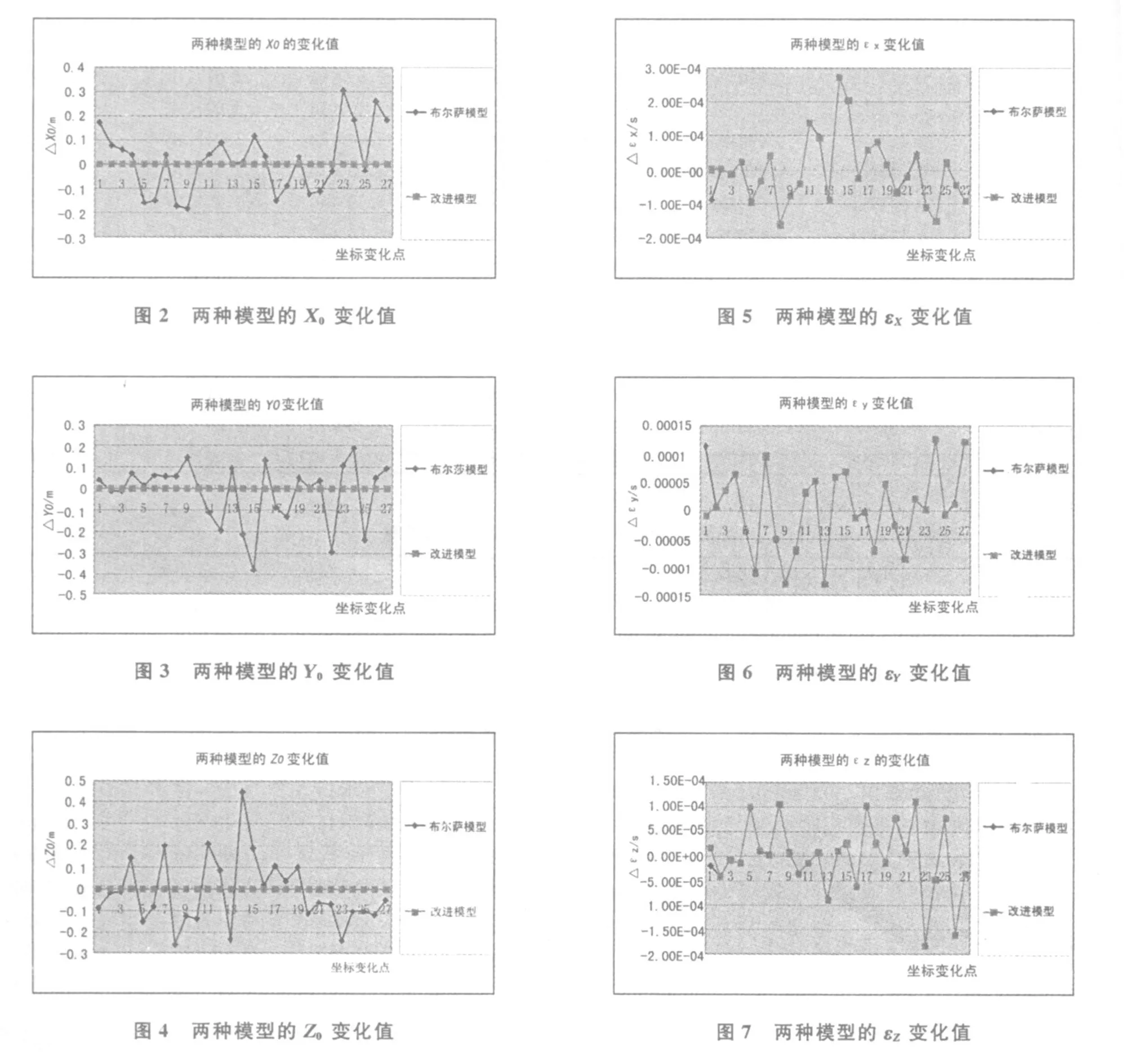
由以上图表可以看出:测区1 mm的坐标误差能引起布尔萨模型平移参数分米级的误差,而只能引起改进模型10-10m级的误差。因此,就GPS厘米级的定位误差来说,布尔萨模型所求得的平移参数会更不稳定,而改进模型的计算结果就稳定多了(实际上对1 cm的误差也做了检验,能引起布尔萨模型平移参数米级的误差,而只能引起改进模型10-10m级的误差)。但两种模型中旋转参数和比例参数的变化值相差不大,基本都在一个数量级上,可见此改正模型对旋转参数和比例参数改进并不大,而对平移参数的影响很大。由此可见,改进模型能大大削弱方程的病态问题,从而大大提高平移参数的稳定性。

4 结 论

对济宁矿区BJ-54至WGS-84坐标转换的布尔萨模型进行了改进,利用实测数据通过fortran编程求出了布尔萨模型和改进模型的七参数,并通过分别改变实测数据的三维坐标引入了微小误差,对这七个参数的变化值分别进行比较。结果表明,改进模型对于平移参数的计算结果比布尔萨模型要稳定很多,而对于旋转参数和比例参数的计算结果两者稳定性相差不大。因此,验证了改进模型能够有效提高平移参数的精度,一定程度上削弱了方程的病态问题,大大提高了平移参数的稳定性,更适用于如济宁矿区这样的小区域的坐标转换。

[1] 范 震.WGS-84至BJ-54坐标转换方法的探讨[J].山西建筑,2008,34(12):354-355.

[2] 刘大杰,施一民,过静珺.全球定位系统(GPS)的原理与数据处理[M].上海:同济大学出版社,1996.

[3] 沈云中,胡雷鸣,李博峰.Bursa模型用于局部区域坐标变换的病态问题及其解法[J].测绘学报,2006,35(2):95-98.

[4] 张秋昭,张书毕,刘 军.局部区域GPS网坐标转换的改进模型[J].全球定位系统,2008,33(5):62-64.

[5] 武汉大学测绘学院测量平差学科组.误差理论与测量平差基础[M].武汉:武汉大学出版社,2003,1.

[6] 张华海,王宝山,赵长胜等.应用大地测量学[M].徐州:中国矿业大学出版社,2007.