载波相位确定模糊度及其误差校正方法①

郭思远,林 翔

(北京5128信箱,北京100094)

0 引 言

载波相位平滑伪距测量方法广泛用于GPS或GNSS接收器。在单频接收机中,为了避免电离层折射效应影响测量精度,平滑时间一般限定为1～2 min的时间。如果应用两个或多个的频率,伪距测量值就可以通过含有电离层折射因素的载波相位测量线性组合平滑。在伪距观测值误差很小的情况下,经过平滑后的伪距观测值可用于测定整周模糊度。如果有三个或以上的不同频率的载波用于测量,就可以组成两组不同的载波相位测量,模糊度可以通过两组滤波方程的差分得到。但是,利用这种方法虽然可以提高确定模糊度的准确性,但是也加大了系统的噪声影响。如果两个频率相近,则消除电离层效应的方程式组合将扩大噪声影响。所以,就要用另外一组折射校正载波相位测量与原有的测量差分,以抵消噪声误差。

1 假设条件

假设两个前提条件:

1)站点与站点之间的测量是完全相同的(从理论上说,这个过程可以用在单一现场测量)。如果一个已知站点坐标,就可以确定任何码和载波偏差,并且能够将它们作为接收点对于卫星坐标的角度函数,这样就可以进行单点测量。经过校准后,方程式就可以在多点测量或者单点测量中应用。

2)假设卫星与卫星之间的测量完全一致。卫星接收器前端过滤器会产生由于不同频率而造成的钟差。这会造成宽巷载波测量和与之相匹配码测量之间的误差。如果这种偏差很大,就会导致模糊度确定误差。我们可以通过卫星间的单差解决这个问题。

由于对流层对不同频率的影响是相同的,在测量过程中电离层折射影响是比较明显的。在模糊度计算和折射校正线性组合中,对流层因素影响不变。这样无几何模型的优势就在于对流层因素并不会对计算过程造成太大影响。

2 宽巷组合模糊度计算[3]

首先进行两组低噪声、折射影响较小、确定模糊度的载波相位测量,以构建两组宽巷载波相位确定模糊度。为了避免相同公式中用许多不同的频率符号,以fa,fb和fc表示。

这两组方程式中,ρ是实际距离(包含对流层折射),I表示为不同频率引起的电离层影响。同样,在载波测量中,可以列式

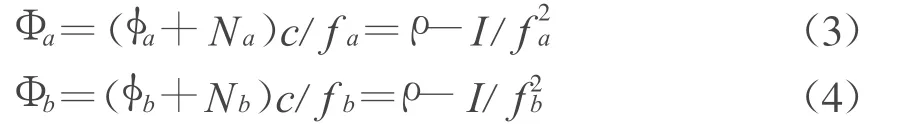
Φa和 Φb为相位值,φa和φb为测量值,N表示载波的起始整周模糊度,c表示光速,在式(1)和式(2)中采用加权平均方法,就能够消去方程式中多路径影响,并有效地表示电离层影响。

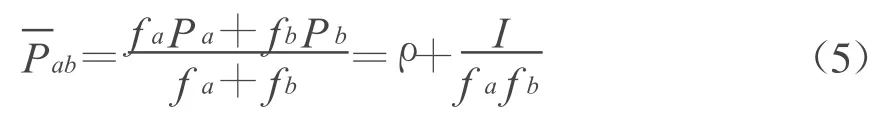
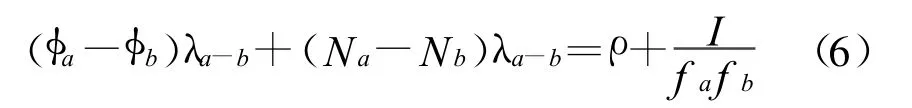
λa-b表示频率差值的波长。由式(5)、(6)可以得出以下方程

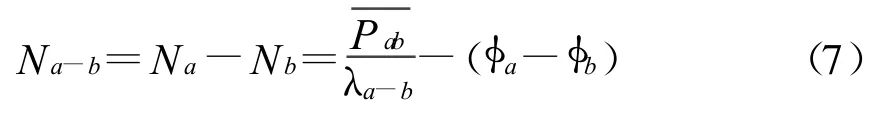
从式(7)中可以看出,只要信号接收器的相位锁定保持稳定,那么宽巷模糊度就不会改变 。那么,这个值就可以采用加权方法获得更准确的值。

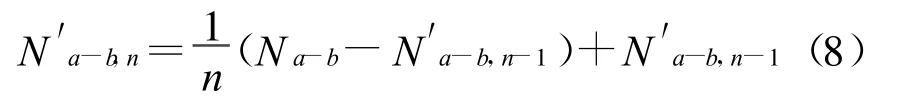
加权后的值可以带进式(6)中进行宽巷载波相位测量

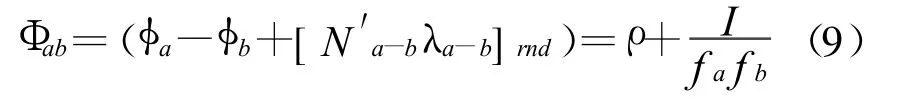
式(8)中为了保证准确的宽巷模糊度,就要保证式N的数量。表1给出了两种不同系统的相关频率的波长。GPS的 L1频率和 L5频率表示为fa和fc,中间频率 fb则由两种频率表示,GPS L2,伽利略E6均比L2频率高51.15MHz。

表1 GPS与Galileo系统波长比较

3 宽巷载波相位测量折射校正

上一节中式(9)表示宽巷测量中由电离层影响引起的误差。这个误差需要校正。首先从三个相位测量中建立第二个模糊度确定宽巷载波测量方程。因为三个不同频率能组合两组不相关的宽巷频率,那么也就能组成两组有最大频率宽度的宽巷组合,就可以用最短时间计算模糊度。

假设 fa＞fb＞fc,宽巷组合由 fb-fc表示,在式(9)中只需要将下标改成b、c,确定了 Na-b和Nb-c的值,Na-c就可以相加得到。所以,第三个载波测量值也就可以得到了。

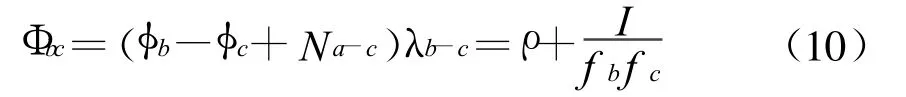
这两个方程式中电离层因素是不同的,所以利用线性组合消去电离层因素影响。将式(10)乘以fc/fa并减去式(9),得

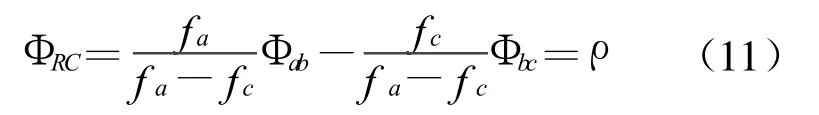
这个方程是没有电离层因素影响的,已进行折射校正模糊度确定的方程式。

4 消除噪声误差[5]

减少折射误差的过程引起了噪声误差在方程式的扩大。在三个宽巷频率之中,各自之间的噪声误差是不相关的。假设,在各个载波相位测量中都可以确定模糊度(将它们表示为 Φa,Φb,Φc),可以得到方程式:

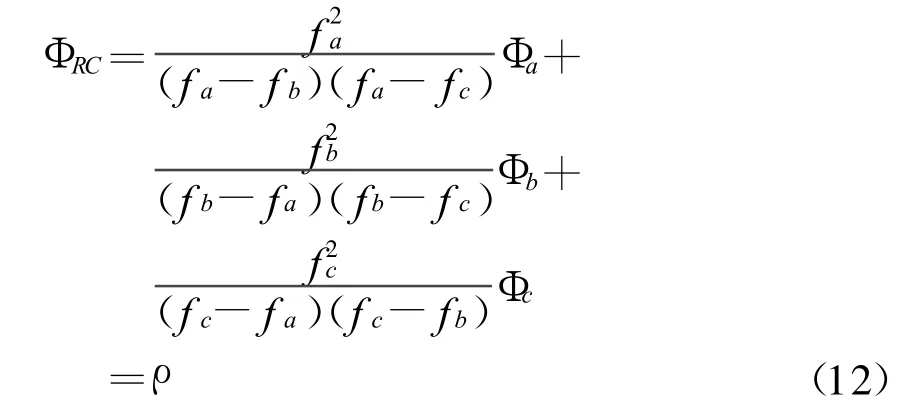
以L1和L5为例,与GPS和Galileo相似。表示为FA和FB频率,可以看到噪声误差是作为中间频率FB的一个函数。假设相位测量中确定波长时,在各个测量中有相当于1 cm的噪声误差;假设各个测量中噪声误差是相同的。那么就能用波长表示噪声误差,如1.0、fc/fa,1.34 cm三种方式。虽然这个误差很小,但是包括了多路径误差效应。测量中预想的噪声误差是方程式(12)中的三个系数的平方和的平方根的值。表2给出了两种不同中间频率所产生的噪声误差,当每个相位噪声都是1 cm,从表2可以看出,Galileo E6频率的噪声误差比GPS L2频率噪声要小的多。

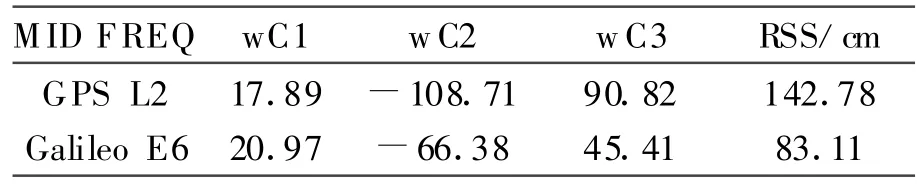
表2 GPS L2与Galileo E6中间频率噪声误差比较

5 载波平滑载波

既然载波相位可以平滑伪距测量,那么可以利用另外一组低噪声,已知整周模糊度的载波平滑式(10)生成的载波测量,来减小噪声误差。

假设每个相位测量噪声误差为1 cm,那么,低噪声,折射校正方程式可以归结为三个因素。上述方程式中的a,b,c必须满足以下三个条件:

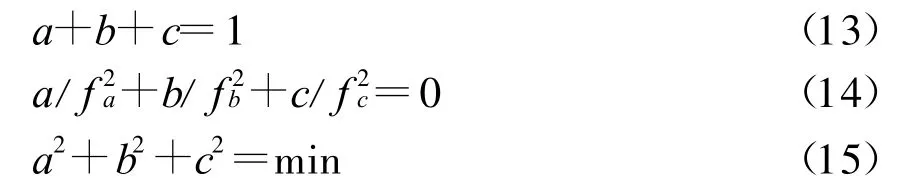
第一个方程保证测量范围不被压缩,第二个方程保证消除了电离层误差。第三个方程则是放大低噪声。由式(13)式可得

将c代入式(14),则

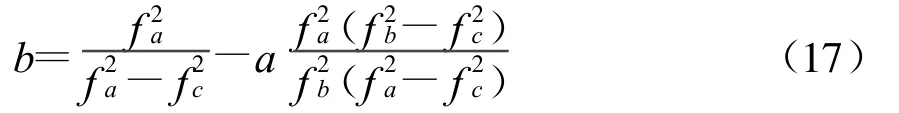
将式(17)简化为

将式(16)、(18)式代入式(15),可得出最小值v

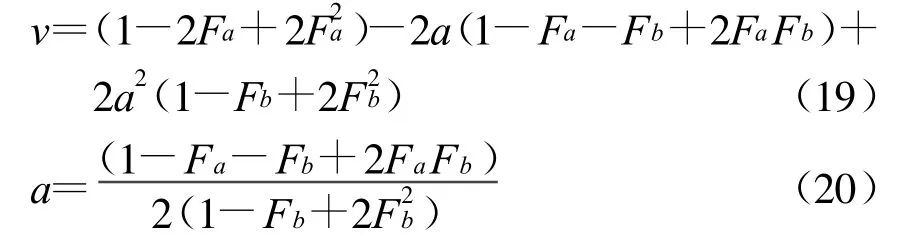
将b和c的值带回式(18)、(16),如果中间频率为上述频率时,表3列出了a,b,c的值和噪声影响。从表3可以看出,当模糊度确定时,GPS L2频率的噪声误差比Galileo E6要小。

表3 模糊度确定时GPS与Galileo系统噪声误差

ΦM假设为最小噪声误差,那么可以列式:

式(11)结果和式(21)结果都含有折射校正误差。将两式相减,得到的结果是三频噪声误差和(21)式中的模糊度初始误差。用O表示为

通过加权方法计算O,那么它的值将会近似于式(21)的误差。

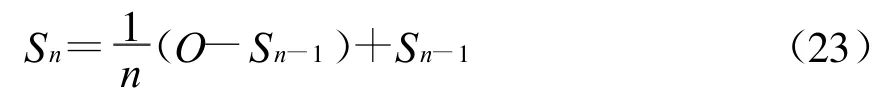
然后再将得出的值带进式(21),得

6 结 论

载波相位平滑伪距测量在伪距观测值误差很小的情况下,经过平滑后的伪距观测值可用于测定整周模糊度。在三个或者以上不同频率的载波测量时,可以利用两组不同载波相位测量,模糊度就可以通过两组滤波方程的差分得到。运用这种方法的同时也加大了系统的噪声影响(如果两个频率相近,则消除电离层效应的方程式组合将扩大噪声影响)。利用了另外一组折射校正载波相位测量与原有的测量进行差分以抵消噪声误差。

[1] 常 青 ,柳重堪,张其善.GPS载波相位组合观测值理论研究1[M].航空学报 ,1998,19(5):12-161

[2] 魏子卿,葛茂荣.GPS相对定位数学模型[M].北京:测绘出版社,1997.

[3] 杨 剑.利用GPS三频组合观测值求解模糊度理论及算法研究1[M].武汉:武汉大学,2004.

[4] 伍岳.第二代导航卫星系统多频数据处理理论及应用[D].武汉:武汉大学,2005,71-76.

[5] Navcom Tech Inc.Method for using three GPS frequencies to resolve carrier-phase integer ambiguities US:1864078[P].Nov 15,2006.