多种微分方程数值计算方法分析

王建强，沈愉乐

(1.武汉大学测绘学院，湖北武汉 430072； 2.吴江市建设房产测量有限公司，江苏吴江 215200)

多种微分方程数值计算方法分析

王建强1∗，沈愉乐2

(1.武汉大学测绘学院，湖北武汉 430072； 2.吴江市建设房产测量有限公司，江苏吴江 215200)

数值微分方程的数值解法是计算方法、数值分析理论中非常重要的内容，数值微分方法也是解决实际计算问题的重要方法。本文对几种常用的数值微分方法进行了简要的分析，并用这几种方法对具有光滑性质的被积函数进行数值计算，龙格－库塔方法和4阶阿达姆斯方法的数值计算稳定性和计算精度都比较好。

微分方程；计算方法；数值分析；数值实验

1 引 言

在科学研究和工程应用中，所建立的数学模型多是常微分方程或微分方程组，但是除了少数特殊类型的微分方程能用解析方法求得其精确解外，大多数情况下要得出解的解析表达式是极其困难的，因此，就需要用数值逼近方法求得其近似解。微分方程组的数值解的存在性和稳定性取决于被积函数的特性和初值。求初值问题的数值解法可区分为两大类:单步法和多步法。常用的方法中欧拉(Euler)方法、改进的欧拉方法、龙格－库塔方法(Runge－Kutta)等[1～4]是单步法的典型代表，线性多步法是多步法的典型代表，对于一些特别的数值微分方程使用这些方法效果很差[5，6]。微分方程的数值解法有显式解和隐式解法，一般来说，隐式解要优于显式解[4]。欧拉方法是一种最简单的单步法，计算量小，但精度比较低。一般的初值问题，多采用改进的欧拉方法，因为它的数值稳定性和计算精度都比一般的欧拉方法好。龙格－库塔方法是一类应用较广的高精度单步法，当解充分光滑时的4阶龙格－库塔方法一般可以达到很高的精度。常微分方程的初值对计算方法的收敛是有影响的[7]。为了更好地比较这几种常用的方法，本文采用这几种数值方法对被积函数光滑连续，初值精确的微分方程做了数值试验。

2 数值计算方法

本文直接给出这几种方法的公式，具体推导过程见文献[3]。

欧拉方法是常微分方程初值问题解中最简单的方法。欧拉折线公式具有1阶代数精度及其改进形式:

式(1)中，k为节点序列，h为步长，f(x，y)为已知函数。两步欧拉方法具有2阶代数精度:

改进的欧拉方法，即欧拉方法的隐式公式:

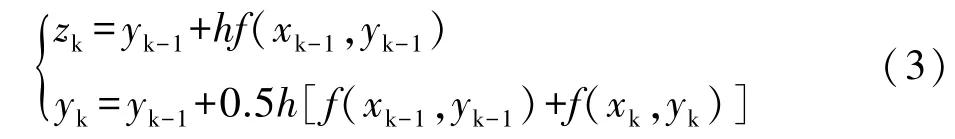
改进的欧拉方法是一个预报－校正的公式，它的稳定性要有余两步欧拉方法。龙格－库塔方法有多种形式，并且有多种阶数，常用的是标准4阶龙格－库塔法。龙格－库塔方法的推导基于泰勒(Taylor)级数展开，它要求方程解具有良好的光滑性质。反之，如果解的光滑性差，使用4阶龙格－库塔方法求得的数值解，其精度可能不如2阶改进的欧拉方法。

以上4种方法都是单步法，由于线性多步法需要利用前面的若干个点，所以初始计算时使用单步法计算得到若干个点，再利用多步法进行计算，一般使用龙格－库塔作为初始计算方法。利用辛普森公式建立的递推公式为:

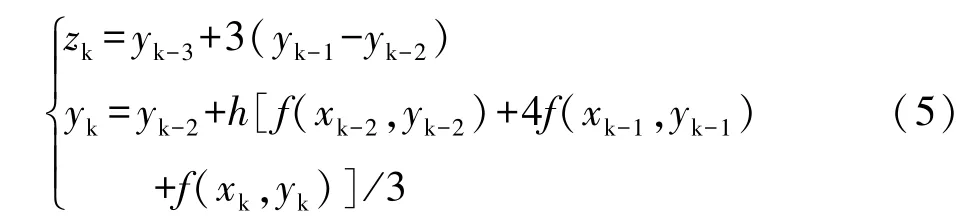
如果只计算一次，这是一个预报－校正方法。实际计算时可以进行多次迭代，迭代次数不宜过多，本文迭代计算两次。在线性多步法的应用中，目前最常用的方法为4阶阿达姆斯(Adams)外推于内插法所形成的预报－校正方法。

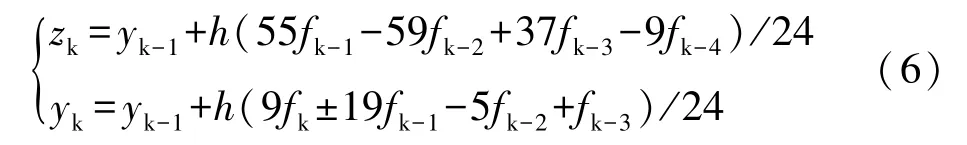
由于多步法计算需要前面几步的数值解，公式(5)需要前面的3步，公式(6)需要前面的4步，因此数值计算时用龙格－库塔作为初始计算起始时的几步数值解。

3 计算分析

利用以上6种方法，计算了两个微分方程，这两个微分方程都有解析表达式，因此可以求出积分误差。第一个微分方程为:

它的解析式为:

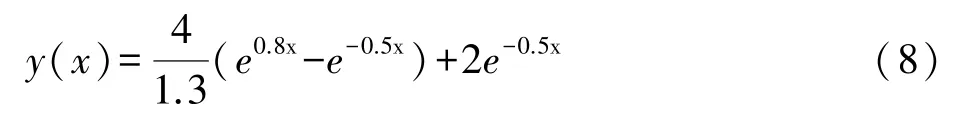
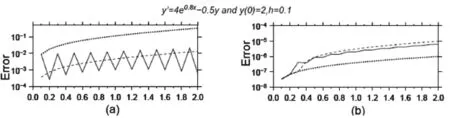
图1 试验1误差曲线(h＝0.1)

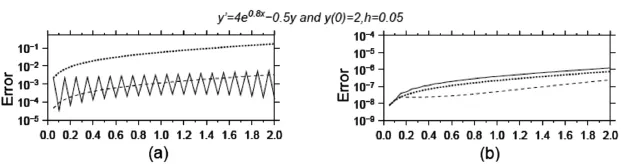
图2 试验1误差曲线(h＝0.05)

通过数值计算结果如图1、图2所示。图1和图2分别是步长h＝0.1和h＝0.05的计算结果。在图1和图2中，(a)图中的点线曲线是由欧拉折线公式计算的结果，精度最低，可以精确到小数点后1位。实线是由两步欧拉方法计算的结果，它比欧拉折线公式得到结果精度要高，可以精确到小数点后2位，从图中可以看出它的误差有明显的振荡，而不是随着k值的增加而增加，表明计算方法的数值稳定性不好。虚线表示改进的欧拉方法，它的计算精度和两步欧拉方法基本相同，在有些点上甚至不如两步欧拉方法，但是它的误差随着 k的增加而增加，数值计算的稳定性较好。(b)图中的点线是龙格－库塔计算的结果，它的误差随着k的增加而增加，数值计算的稳定性较好，实线是辛普森公式建立的递推公式的结果，它的误差有较小的振荡，虚线的是4阶阿达姆斯方法求得的数值解。从图1和图2中可以看出，当步长减小后，4阶阿达姆斯方法计算精度提高得最明显。

第二个微分方程:

它的解析表达式为:

通过数值计算结果如图3、图4所示。图3和图4分别是步长h＝0.1和h＝0.05的计算结果，图中的不同曲线和图1、图2中曲线代表的计算方法相同。计算方法的精度和前一个试验相当，在这个试验中，h＝0.1时，龙格－库塔方法的计算精度比4阶阿达姆斯的差，而在h＝0.05是，4阶阿达姆斯的计算精度比龙格－库塔法、辛普生方法精度都要低，计算精度的提高最不明显。

对这两个数值试验，从图1～图4中可以看出，对于解比较光滑的曲线，龙格－库塔法、4阶阿达姆斯方法和辛普生方法的计算精度比欧拉方法、两步欧拉方法和改进的欧拉方法要高一个数量级。辛普生方法的积分误差曲线存在较小的波动，数值稳定性不好，4阶阿达姆斯方法和龙格－库塔法的误差曲线随着步长的增加而增加，数值稳定性较好。从这两个试验中，随着步长的减小，计算精度的提高随着微分方程、计算方法的不同而不同。

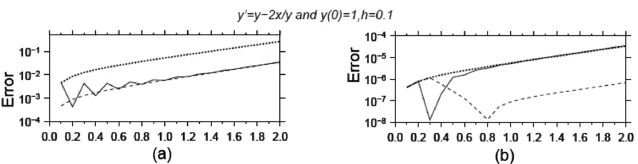
图3 试验2误差曲线(h＝0.1)

图4 试验2误差曲线(h＝0.05)

4 结 论

通过理论分析和两个数值试验可以得出，数值微分方程的隐式解比同阶的显式解的数值稳定性要好，龙格－库塔法、辛普生方法和4阶阿达姆斯方法具有较高的代数精度，可以得到比较好的结果。数值微分方程的数值解有很多种方法，建议使用计算精度较高，稳定性较好的数值计算方法，比如龙格－库塔法、4阶阿达姆斯方法等，并且有必要使用多种方法做检核。

[1]奚梅成.数值分析方法[M].北京:中国科学技术大学出版社，2003

[2]王能超.计算方法简明教程[M].北京:高等教育出版社，2004

[3]甄西丰.实用数值计算方法[M].北京:清华大学出版社，2006

[4]吴勃英.数值分析[M].北京:高等教育出版社，2007

[5]Iserles A.On the Method of Neumann Series for Highly Oscillating Equations[J].BIT，2004，44:473～488

[6]Iserles A.On the Global Error of Discretization Methods for Highly－Oscillatory Ordinary Differential Equations[J]. BIT，2002，42:561～599

[7]陈清明.Banach空间常微分方程初值问题弱解的一个逼近定理[J].西南大学学报(自然科学版)，30(4):49～52.关于初值问题的解的探讨.

Numerical Calculation Analysis on Different Methods of Differential Equation

Wang JianQiang1，Shen YuLe2
(1.School of Geodesy and Geomatics，Wuhan University，Wuhan 430079，China；2.Wujiang construction and real estate of survey Co.，Ltd.Wujiang 215200，China)

Numerical solution of differential equations is the very important content of numerical calculation method and numerical analysis，and numerical differentiation method is important to solve practical computing problems.In this paper，several commonly used methods of numerical differentiation are given a brief analysis and use these methods with the integrand is smooth to carry out numerical experiments，Runge－Kutta method and fourth－order Adams method Numerical calculation are better than others with the stability and calculation accuracy.

differential equation；calculation method；numerical analysis；numerical experiment

1672－8262(2010)04－117－03

O175

A

2009—12—26

王建强(1981—)，男，博士研究生，研究方向为全球重力场模型研究。