杭州市住宅价格空间分异：基于特征价格的两维度分析

温海珍，张 凌，彭鲁凤

（浙江大学房地产研究中心，浙江 杭州 310027）

1 引言

随着中国住房制度改革的深化，住宅市场化程度逐步加深，住宅价格已经成为学术界和实务界关注的焦点之一。对城市住宅空间分异研究，通常以居住空间为对象，从社会学视角进行［1-2］。而以住宅价格为对象，从经济学视角入手的空间分异研究尚不多见，特别是缺少对具体城市的实证研究。现有文献多从区位理论出发，研究住宅价格的分布规律，然后分析住宅价格的影响因素［3-5］。这些研究对住宅价格的空间分布模式进行了较为详细地分析，但对住宅价格的影响因素和空间分异形成的原因，缺少系统的分析框架。本文尝试从特征价格的视角，采用特征价格模型和隔离指数，构建住宅价格空间分异的两维度分析框架，对杭州市住宅市场进行实证研究。

2 住宅价格空间分异的两维度分析框架

城市住宅是一种“独特”的产品［6］，具有复杂性、固定性、耐久性、异质性等特点。住宅价格的影响因素十分复杂，与住宅本身的特征关系密切。从特征价格视角出发，住宅特征是住宅价格的决定因素，由于住宅的空间固定性，使得住宅特征在空间分布上存在差异，从而导致住宅价格的空间分异。因此，本文面临的问题包括两个方面，一是住宅特征如何影响住宅价格；二是如何考察住宅特征的空间分布，进而找出住宅价格空间分异的原因。

第一个问题构建特征价格模型即可获得满意结果。众多文献表明住宅特征一般分为3类：建筑特征、邻里特征和区位特征，Chin和Chau［7］，Sirmans，et al［8］分别就特征变量的选择、模型的设定和估计、住宅特征的影响程度等作了全面的总结，具有很好的参考价值。国内学者马思新、李昂［9］采用特征价格模型对北京住宅价格的影响因素进行了分析；温海珍、贾生华［10］对杭州西湖区进行了初步研究；此后wen，et al［11］对杭州市整个住宅市场进行了更为详细的研究，选择18个住宅特征作为模型的自变量，发现其中14个特征变量对住宅价格具有显著影响。

第二个问题可以采用隔离指数对住宅特征的空间分异程度进行定量测算。在城市地理学和城市社会学中，常常采用隔离指数衡量某一变量在空间上的异质性程度。自从Duncan在1955年提出该指数后，房地产领域经常用其评价住宅市场隔离的空间均匀程度［12-13］。隔离指数的计算公式为：

式1中，xi为区域i内某一类住宅占所有同类住宅的比例；yi为区域i内所有其他类型住宅占全部空间范围内所有其他类型住宅的比例；N为空间区域的分类总数。当住宅特征的空间分布完全均匀时，DI=0；当住宅特征的空间分布处于极端分异时，DI=1；一般DI的数值在0和1之间变动，隔离指数越大，住宅特征的空间分布越不均匀。

3 特征价格模型设定

3.1 数据与研究区域

本文选择杭州市主城区范围内的上城区、下城区、拱墅区、江干区、西湖区5个老城区作为实证研究区域。从杭州市房地产中介服务公司获得从2003年1月1日至2003年7月31日的住宅样本数量总计4063个，选择多层住宅和小高层作为研究对象，并对样本数据的完备性进行检查，有效样本2473个。笔者在2003年6月30日至2003年8月18日期间，对研究区域进行了实地调查。最后，通过筛选得到235个有效的住宅小区样本。

3.2 住宅特征的选择及量化

国外对住宅市场进行特征价格研究时，住宅特征变量一般分为3大类，即建筑特征、邻里特征和区位特征。结合杭州市的实际情况，本研究选择了11个住宅特征作为模型的自变量，因变量则采用住宅均价（所在小区住宅单位价格的平均值）。特征变量的量化以及对住宅价格的预期影响符号见表1。

3.3 函数形式和估计方法

特征价格模型常用的函数主要有线性和对数两种形式。在本研究中连续变量有住宅均价（因变量）、CBD距离和西湖距离（自变量），这3个变量可以采用线性或对数形式，其余变量均为等级变量，一般采用线性形式。因此，可能的函数形式有4种。通过模型的试构建，比较模型的拟合效果和显著性变量的个数，最后选择的函数形式是因变量为对数形式、自变量CBD距离和西湖距离为对数形式，其余变量为线性形式。

模型的估计方法为最常用的最小二乘法（OLS）。在SPSS软件中选择强行进入法（Enter）作为回归分析方法，即所选择的自变量全部进入回归模型。同时，采用方差膨胀因子（VIF）对变量之间的共线性进行监测。

表1 住宅特征变量的量化Tab.1 Quantification of housing characteristic variables

4 结果与讨论

4.1 住宅价格空间分异特征

图1 杭州市住宅价格等值线Fig.1 Isoplethes of housing prices in Hangzhou City

通过GIS软件，绘制杭州市住宅价格空间分布的等值线（图1），发现2003年杭州市住宅价格空间分布总体上具有以下几个特点：（1）住宅价格的空间分布，总体呈现以西湖为核心、向周边梯度下降的格局。值得注意的是，价格下降幅度并非连续递减趋势，从西湖出发向东、向北、向西北三个方向分别绘制住宅价格剖面图发现：距离西湖1.0—1.5km之间出现带状的相对的价格小低谷，在1.5—2.5km处又突现一系列价格高峰，之后向城市外围快速下降。（2）城市CBD成为杭州市住宅价格的次核心，传统老城区构筑了住宅价格的中高平台。武林广场作为中央商务区（CBD），其周边区域的住宅价格都比较高，使得整个杭州的高价住宅区域由西湖向北延伸了2km。传统老城区由于受到西面西湖和北面武林广场的辐射作用，具有较大的区位优势，价格呈现连续的中高价块状分布。（3）住宅价格分布呈现多个次中心，总体上环绕西湖分布。从图1中可以看出，除了西湖和武林广场两大价格核心以外，多个价格次中心已经出现。如城西蒋村，该区域是杭州市商品住宅开发的密集区域，在早期政策的指引下，已发展得较为成熟。其住宅价格形成了一个较为独立的中高价区域，并有向北延伸的趋势。（4）穿城铁路的阻隔效应和运河的环境效应显著。铁路从杭州东面穿城而过，铁路东面的住宅价格明显低于铁路西面。城东采荷和南肖埠区域的住宅价格延续了老城区的高价，是江干区惟一的中高价区域。而望江区域（杭州火车站东南面）价格较低，从区位上来说这里离西湖和钱塘江都较近，价格理应较高，但是由于铁路线的阻隔以及没有有效的道路通行，价格受到较大影响。运河沿线住宅价格较高，在环境偏差的拱墅区尤为明显，主要是由于运河的自然环境效应使得住宅的价格上升。

4.2 特征价格价格模型的检验

采用SPSS软件对特征价格模型进行估计，发现回归方程的F值显著性水平小于0.001，修正的R2为0.666，说明模型的拟合程度可行。模型D—W值为1.751，可以判断基本不存在异方差问题。所有变量的VIF值均小于10，说明自变量之间共线性程度不严重。总体上，模型具有较高的解释能力，在统计上是有意义的。

就单个自变量的t检验来看，在10％的显著性水平下，11个自变量中有7个进入了模型。自然环境、公交线路、邻近大学、教育配套等4个变量的显著性水平均大于10％，因此从统计意义来看，其回归系数与零没有差异。7个显著性变量的符号与预期符号完全一样。其中小区环境、生活配套、文体设施、治安环境对住宅价格有正影响，建筑房龄、CBD距离和西湖距离则对住宅价格有负影响。

4.3 住宅特征的影响程度分析

表2 模型估计和影响因素Tab.2 Model estimation and influencing factors

住宅特征变量由于单位不同，各特征对小区价格的影响程度无法进行直接比较。但是，标准化后的回归系数是所有变量进行标准化（Z分数）后得到的，可以使用它的绝对值来进行各特征影响程度的排序。本文将住宅特征分为4类，分类的标准为：|Beta|≥0.200为第1类；|Beta|≥0.100为第2类；|Beta|≥0.050为第3类；|Beta|＜0.050为第4类。排序和分类的具体数值见表2。

结果表明，11个住宅特征对住宅价格的影响程度是有差异的，影响程度最大的住宅特征是西湖距离，最小的是邻近大学。第1类对住宅价格的影响最大，共有2个特征，为西湖距离、建筑房龄；第2类有3个特征，为小区环境、CBD距离、治安环境；第3类有2个特征，为生活配套、文体设施；第4类有4个特征，主要是不显著的变量，为教育配套、自然环境、公交线路、邻近大学。

表3 变量编码规则Tab.3 Coding rules of variables

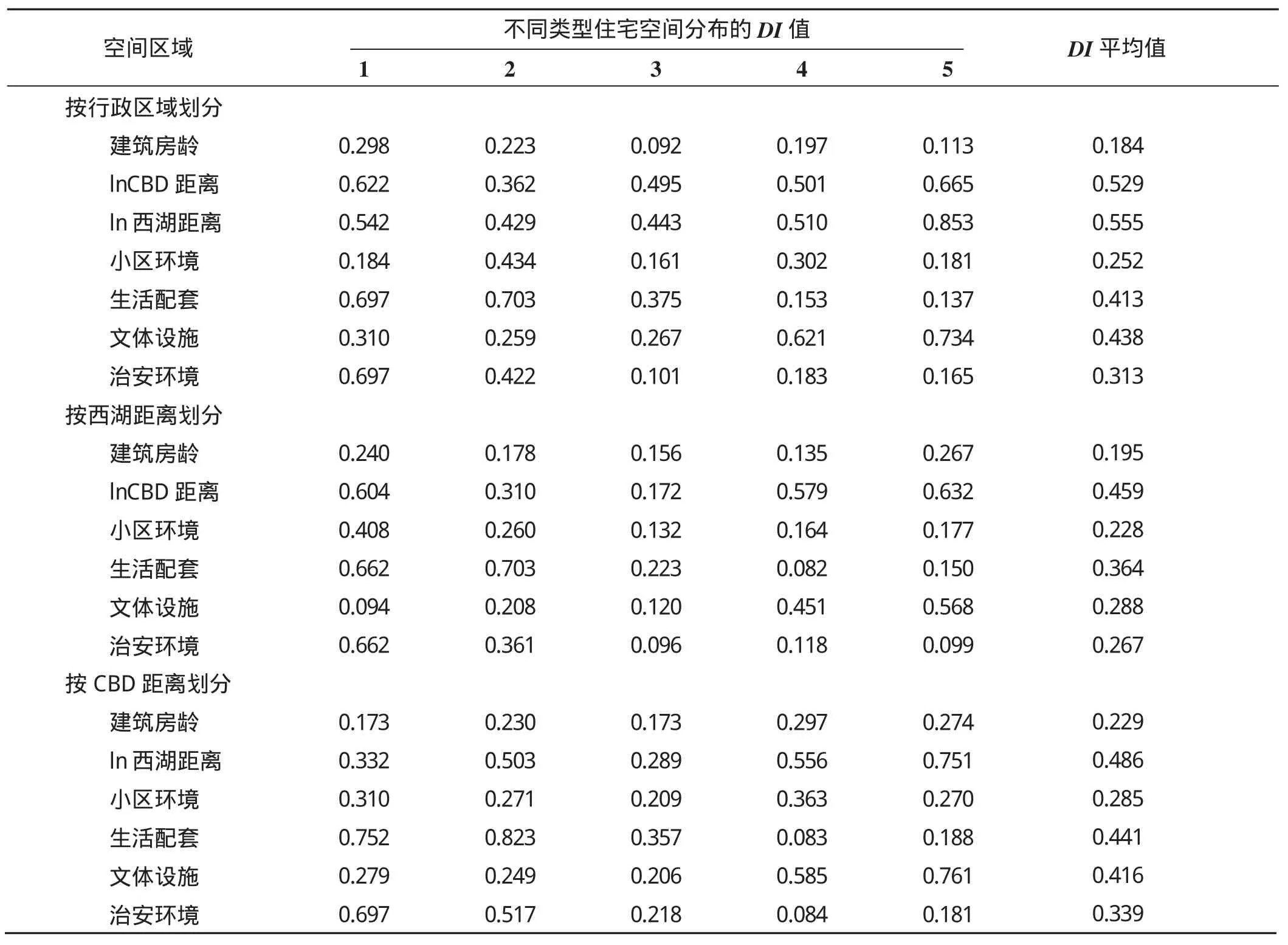
表4 离散指数结果Tab.4 Results of dispersion index

4.4 住宅特征的空间异质性分析

为了计算隔离指数DI并使其与其他特征具有可比性，对建筑房龄、CBD距离和西湖距离进行重新编码，具体规则如表3。

以行政区域、西湖距离、CBD距离作为空间划分的变量，计算得到7个显著特征变量的隔离指数，如表4所示。三种分类的结果均表明，两个区位变量（西湖距离、CBD距离）的隔离指数数值最大，空间分布最具有异质性。住宅年龄、小区环境的隔离指数数值最小，说明这两类住宅特征在空间分布上较为均匀。

5 结论

本文采用Kriging空间内插方法绘制了杭州市住宅价格的等值线，图形表明2003年杭州市住宅价格空间分布总体上呈现以城市景观中心（西湖）为核心、向周边梯度递减的格局，城市CBD成为杭州市住宅价格的次核心，住宅价格分布出现多个次中心，并且穿城铁路的阻隔效应和运河的环境效应显著。

通过构建特征价格模型和计算住宅特征的隔离指数，研究表明住宅特征是住宅价格的决定因素，其空间分布进一步影响住宅价格的空间分异。从住宅特征对住宅价格的影响程度来看，特征变量对住宅价格的影响程度是有差异的，从大到小依次为西湖距离、建筑房龄、小区环境、CBD距离、治安环境、生活配套、运动设施。从住宅特征的空间分异程度来看，空间异质性大的为西湖距离、CBD距离，中等的为小区环境、建筑房龄，小的为治安环境、生活配套、运动设施。

实证研究表明基于特征价格视角的两维度分析框架有效和合理，可以为其他学者进行类似研究提供参考。本文计算隔离指数时采用了常用公式，更为复杂的计算方法也许能得到更细致的结果，有待进一步深入研究。

（References）：

［1］吴启焰，崔功豪.南京市居住空间分异特征及其形成机制［J］.城市规划，1999，23（12）：23-26，35.

［2］刘冰，张晋庆.城市居住空间分异的规划对策研究［J］.城市规划，2002，26（12）：82-86.

［3］许晓晖.上海市商品住宅价格空间分布特征分析［J］.经济地理，1997，17（1）：80-87.

［4］王欣.天津市中心城区商品住宅价格地区分异的研究［J］.天津师范大学学报：自然科学版，2002，22（2）：70-74.

［5］郑芷青.广州市商品住宅价格分布特征研究［J］.热带地理，2001，21（1）：22-26.

［6］Harsman B，Quigley JM.The Spatial Segregation of Ethnic and Demographic Groups：Comparative Evidence from Stockholm and San Francisco［J］.Journal of Urban Economics，1995，37：1-16.

［7］Chin TL，Chau KW.A Critical Review of Literature on the Hedonic Price Model［J］.International Journal for Housing Science and Its Applications，2003，27（2）：145-165.

［8］SirmansGS，Macpherson D A，Zietz E N.The Composition of Hedonic Pricing Models［J］.Journal of Real Estate Literature，2005，13（1）：3-43.

［9］马思新，李昂.基于Hedonic模型的北京住宅价格影响因素分析［J］.土木工程学报，2003，36（9）：59-64.

［10］温海珍，贾生华.住宅的特征与特征的价格——基于特征价格模型的分析［J］.浙大学报（工学版），2004，38（10）：1338-1342，1349.

［11］Wen H Z，Jia SH，Guo X Y.Hedonic Price Analysis of Urban Housing：An Empirical Research on Hangzhou，China［J］.Journal of Zhejiang University（Science），2005，6A（8）：907-914.

［12］Duncan O，Duncan B.A Methodological Analysis of Segregation Indices［J］.American Sociological Review，1955，20：210-217.

［13］Iceland J，Weinberg D H，Steinmetz E.Racial and Ethnic Residential Segregation in the United States：1980-2000［EB/OL］.http://www.census.gov/prod/2002pubs/censr-3.pdf.