某能源中心空调用冷却塔性能的模拟分析

胡建亮,张恩泽,刘东,程勇,马国杰

(同济大学机械工程学院,上海200092)

某汽车生产厂区能源中心共有7台开式逆流式空调用冷却塔,型号均为BFNPDG-2000。冷却塔填料材料为PVC,为点滴薄膜式冷却塔,本文将为冷却塔的运行建立数学模型。这些冷却塔已经运行了多年,为了解该设备的目前的热工性能情况,决定对它的性能进行实测,通过实测数据验证数学模型的准确性,然后利用模型模拟冷却塔在不同环境及运行工况下的性能参数。

1 冷却塔的性能

BFNPDG-2000点滴薄膜式冷却塔,额定冷却水流量2000 m3/h,额定空气入口湿球和干球温度分别为28℃和31.5℃,冷却水进水和出水温度分别为37℃和32℃;冷却塔有4台轴流风机,每台风机功率为18.5 kW。冷却塔的填料层尺寸为11 m ×11 m×1.5 m。空气由冷却塔底部百叶风口引入,从顶部风口排出;冷却水从上往下流动,经过填料层、淋水层,流入冷却塔水池,见图1。

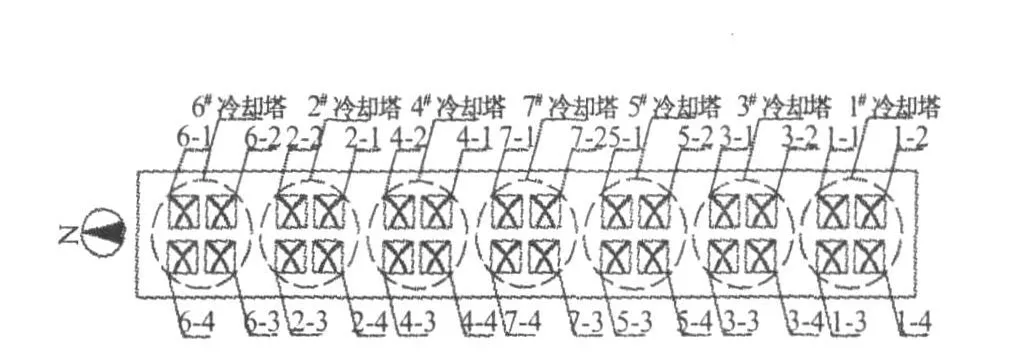
图1 冷却塔布置图

2 冷却塔传热传质基本微分方程

为了分析冷却塔的传热传质,取冷却塔填料层的体积微元d V,见图2。在体积d V段内,空气与水以焓值表示的能量平衡方程[1]:

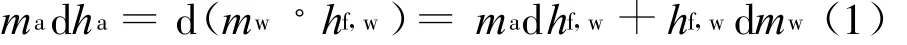
式中:ma为干空气流量;ha为湿空气比焓;mw为冷却水流量;h f,w为冷却水焓值。

在体积d V段内,空气与水的质量平衡方程:

体积元中水的出口流量,等于水的入口流量减去冷却过程中水蒸发损失的水量:

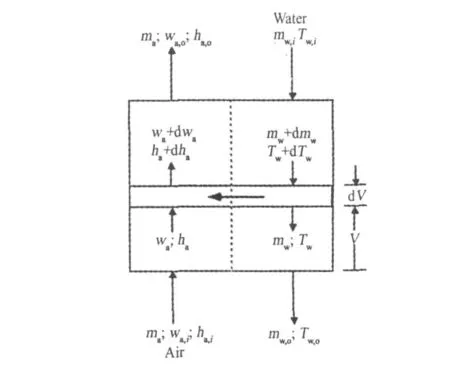
图2 逆流式冷却塔的传热传质微元

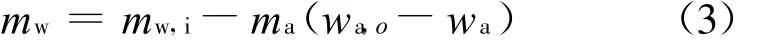
式中:w a为湿空气含湿量;m w,i为冷却水入口流量; wa,o为湿空气出口含湿量。

假设水的比热容cp,w为常数,结合(1)式、(2)式和(3)式在d V段内可得:

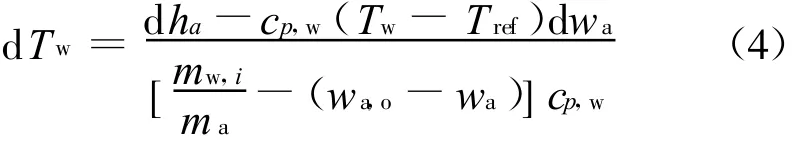
式中:T w为水温,T ref为对应水焓值为零时的温度, c p,w为水的比热容。

空气与水的全热交换是由显热交换和潜热交换两部分组成,因此d V段内全热交换量可写成:

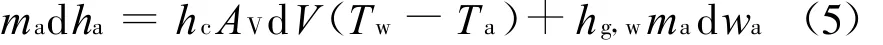
式中:h C为对流传热系数,A V为冷却塔单位体积内的水滴表面积,h g,w为在某温度下水蒸气焓值。

在d V段内,以传质系数表示水的蒸发量:

式中:h D为传质系数,w s,w为在某温度下饱和空气含湿量。

结合(5)式和(6)式,并引入刘易斯数Le可得:

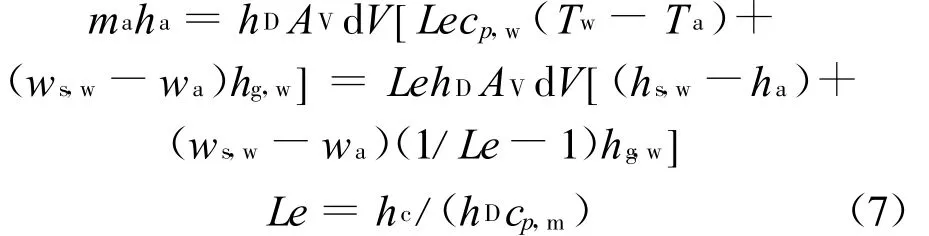
式中:cp,m为湿空气的定压比热容。

根据传质单元数N tu的定义:

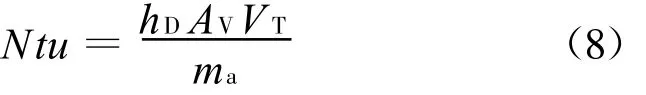
式中:V T为冷却塔填料层总体积。

将(8)式代入(6)式和(7)式,可得:

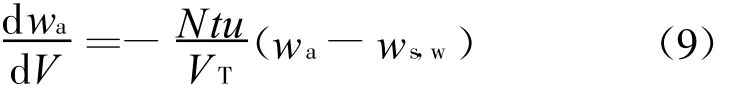
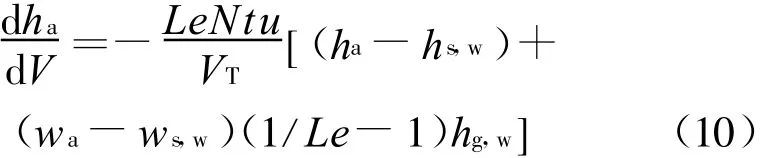
假设水流量没有损失,刘易斯数Le为1,可将式(4)和(9)简化为麦克尔理论关系式:

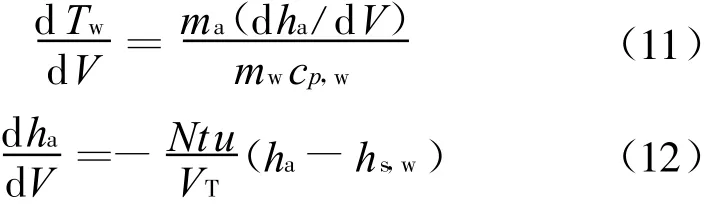
3 冷却塔效率-传热单元数数学模型

为了简化模型,假设只在冷却塔垂直方向发生水与空气的热质交换过程;忽略冷却塔塔壁与环境的热交换;水与空气比热恒定;冷却水在塔内同一水平面温度相同;忽略冷却水在淋水层与湿空气的热质交换;饱和湿空气焓值和对应温度是线性关系。

传热单元数N tu:

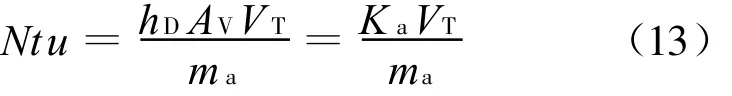
式中的K a为冷却塔淋水填料的容积散质系数,由西安热工研究院提供的经验公式确定:

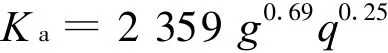
式中:Ka为容积散质系数,kg/(m3·h);g为通风密度(塔进风口处空气平均风速),kg/(m2·h); q为淋水密度,kg/(m2·h)。

该经验公式以实测有效工况点为依据计算各工况点的容积散质系数,用最小二乘法拟合成。使用效率表示的实际传热量Q[2]:

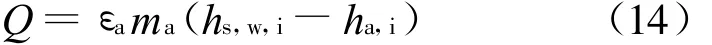
式中:εa为冷却塔空气侧热交换效率;hs,w,i为在进水温度下的饱和湿空气焓值;h a,i为湿空气入口焓值。

利用类比方法,空气侧效率的表达式εa:

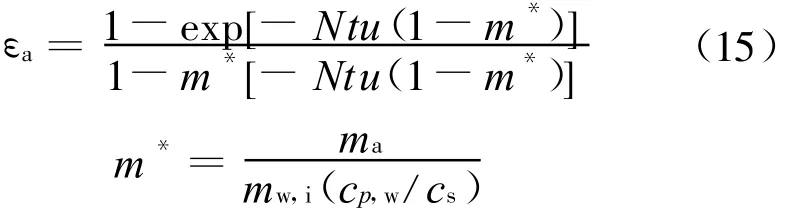
以冷却塔整体为对象,由能量平衡,可得湿空气的出口焓值h a,o:

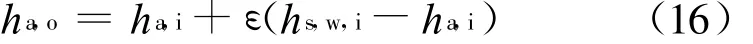
水的出口水温T w,o:

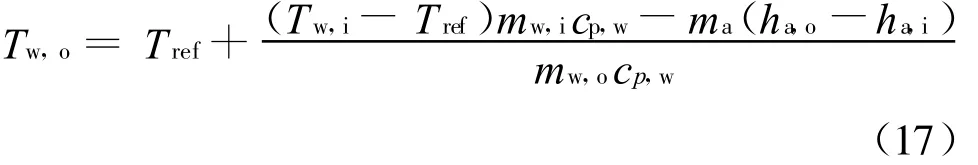
在水入口和出口,空气平均饱和比热容c s:

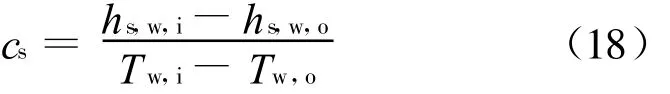
考虑水损失,出口水流量m w,o:

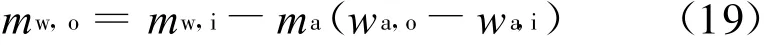
对(9)式积分,得到湿空气出口含湿量w a,o:

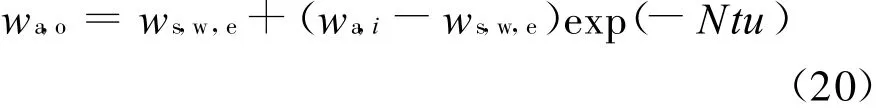
利用效率-传热单元数方法,在MATLAB软件中编程,模拟冷却塔中传热传质过程的模拟见图3。

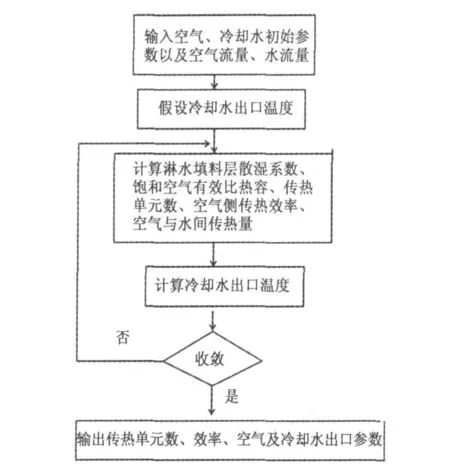
图3 模拟流程图

模型分析方法采用类比显热热交换器的分析方法,并在此基础上引入饱和空气比热容,能够计算塔湿空气含湿量,并且由于考虑了冷却水蒸发损失,因此结果较准确。模型假设饱和空气焓值与温度是线性关系,但在冷却水进出口温差增大时,即气水比增大时,饱和空气焓值与温度的线性关系变差,只有当冷却水进出口温差减小时,即气水比减小时,饱和空气焓值与温度线性关系较好。比较模拟数据和实测数据,可以看到对于冷却水额定温差为5℃的冷却塔,模拟与实测的结果吻合度较好,说明冷却水温差在5℃左右时,饱和空气焓值与温度的线性关系误差较小。

4 模型的验证

为了验证模型的模拟结果对冷却塔的运行参数进行了测定,通过比较冷却塔出水温度以及冷却塔出塔空气焓值来验证能效传热单元数模型的准确性。测试数据共有七组,测试时最高的环境干球温度为35.9℃,最高的环境湿球温度为29.5℃;最低的环境干球温度为32.7℃,最低的环境湿球温度为26.4℃。冷却水流量在冷水机组的冷却水出水管处测得,冷却水进塔水温在冷水机组冷却水出水管处测得,冷却水出塔水温在冷却塔水池处测得,空气进塔及出塔干湿球温度分别在冷却塔空气入口、出口处测得,冷却塔空气流量在冷却塔百叶风口处测得。

图4是冷却水出水温度比较。从图4中可以看到,有五组模拟冷却水出水温度大于实测冷却水出水温度,有两组模拟冷却水出水温度小于实测冷却水出水温度,其中最大出水温度的误差为-1.3℃,最大相对误差为-4.5%;最小出水温度的误差为0.2℃,相对误差为0.6%。

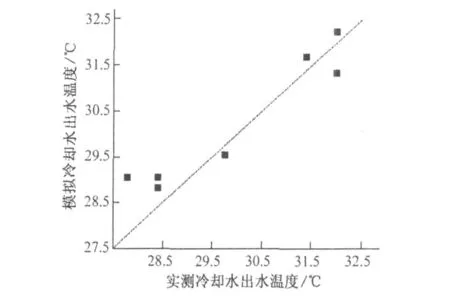
图4 冷却水出水温度比较

图5是冷却塔出塔空气焓值比较。从图5中可以看到,有六组模拟冷却塔出塔空气焓值均小于实测冷却塔出塔空气焓值,有一组模拟冷却塔出塔空气焓值约等于实测冷却塔出塔空气焓值。通过模拟得到的出塔空气焓值小于实测值,这是因为冷却塔漂水使测得的出塔空气含湿量增大,从而使出塔空气焓值偏高。根据分析结果,最大出塔空气焓值误差为8.1 k J/kg(DA),相对误差6.7%;最小出塔空气焓值误差为0.1 k J/kg(DA),相对误差0.07%。比较结果说明,采用该模型对冷却塔的运行进行模拟,模拟的结果是可信的。

图5 冷却塔出塔空气焓值比较

5 设计日时模型对冷却塔的模拟分析

图6为上海市典型气象年夏季设计日早上七点至下午五点环境空气干湿球温度分布,温度分布呈驼峰型;最高干球温度为37.3℃,最高湿球温度为28.9℃,均出现在下午一点钟;最低干球温度为30.4℃,出现在早上七点钟,最低湿球温度为26.5℃,出现在下午五点钟;干球温度最大变化为6.9℃,湿球温度最大变化为2.4℃。

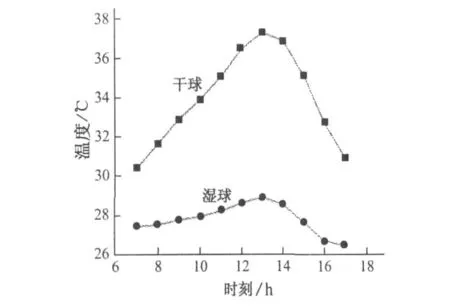
图6 设计日环境空气干湿球温度

图7为在设计日条件下模拟的冷却塔出水温度,其中冷却水入水温度保持为37℃,保持空气流量不变,改变冷却水流量。使得气水比分别为0.75,1.0和1.5。可以看到,随着环境湿球温度的升高,冷却水出水温度也随之升高,并且气水比越高,冷却水出水温度变化幅度越大。当气水比为1.5时,冷却水出水温度最大变化幅度为1.7℃;当气水比为0.75时,冷却水出水温度最大变化幅度为1.1℃。

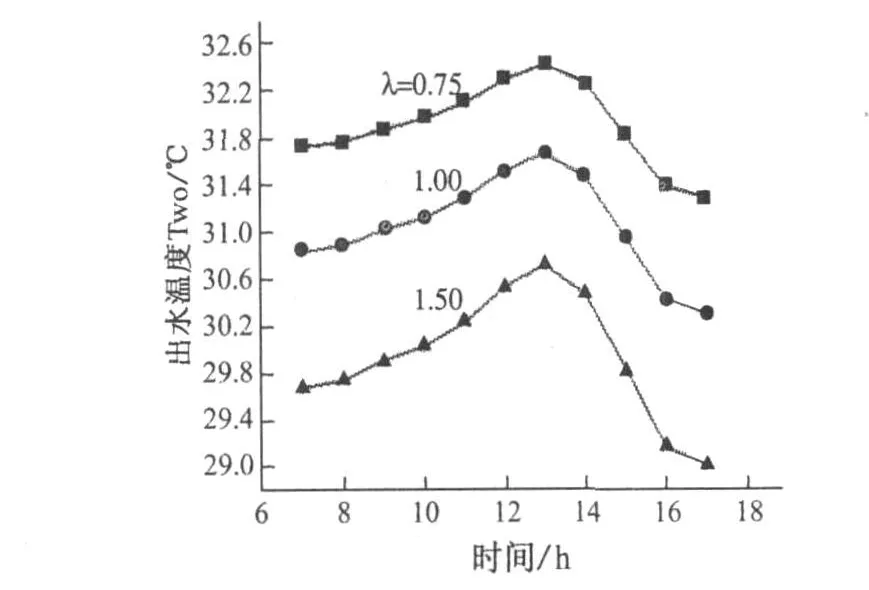
图7 模拟冷却塔出水温度

图8为设计日条件下模拟的冷却塔冷却水侧热交换效率,冷却水侧热交换效率受环境影响较小,当水比为0.75时,水侧热交换效率受环境影响变化幅度最大,为2.3%。冷却水侧热交换效率主要由气水比决定,气水比越大,效率越高;当气水比为1.5时,冷却水侧平均热交换效率为76.9%,当气水比为0.75时,冷却水侧平均热交换效率为55.6%。

图9为设计日条件下模拟的冷却塔实际散热量占额定散热量的比例。散热量分布呈下凹形状。冷却塔散热量与环境工况以及气水比都有很大关系。在同一气水比条件下,中午时刻散热量小,早上七、八点和下午四、五点时散热量大,特别是下午四、五点时的散热量比早上七、八点时的散热量要更大,说明冷却塔散热量受环境湿球温度的影响大于环境干球温度的影响。当气水比为0.75时,冷却塔散热量随环境工况变化的幅度最大,为22.8%。对于相同的环境工况,气水比越大,冷却塔散热能力越小。当气水比为 0.75时,冷却塔散热能力最大为114.3%,散热能力最小为91.5%;当气水比为1.5时,冷却塔散热能力最大为79.9%,散热能力最小为62.8%。

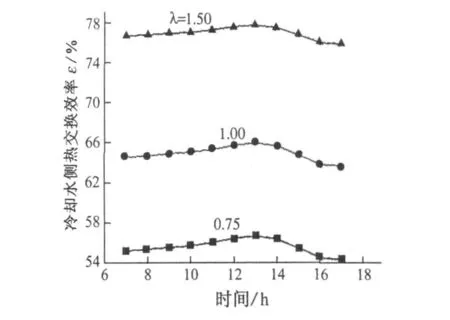
图8 模拟冷却塔冷却水侧热交换效率

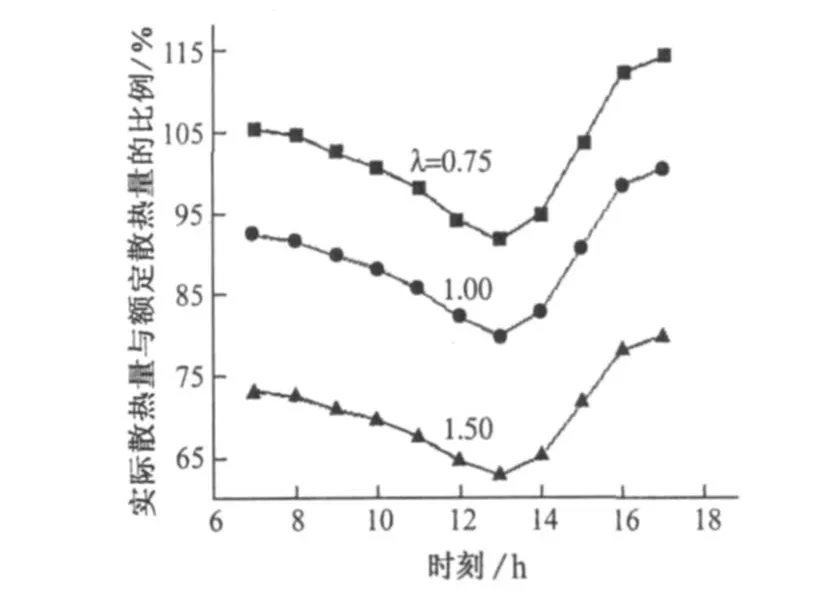
图9 模拟冷却塔实际散热量

6 结论

(1)利用效率-传热单元数理论建立的数学模型能够模拟冷却塔内传热传质过程,并且模拟的结果较准确。

(2)从冷却塔设计日逐时模拟的结果可见,冷却塔出水温度和冷却塔散热量不仅与环境工况有关,尤其与环境湿球温度有较大关系,也与冷却塔气水比有较大关系。冷却塔冷却水侧热交换效率与冷却塔气水比关系较大,但与环境工况的相关性较小。

[1] SUTHERLAND JW.Ana lysis o fmechanical d raught counterflow air/w ater cooling towers[J].Journal of Heat T ransfer,1983,105:576-583.

[2] BRAUN JE,KLEIN SA,M ITCHELL JW.Effectiveness Models for Cooling Tow ers and Cooling Coils [J].ASHRAE Transactions,1989,95(2):164.