基于二元超阈值模型的空调室外计算干湿球温度确定方法研究
刘艳峰,吴美玲,王莹莹,周 勇
(西安建筑科技大学 建筑设备科学与工程学院,陕西 西安 710055)
空调设计计算干、湿球温度是建筑空调系统设计的数据基础.目前,空调室外计算干,湿球温度主要由气象单参数的一维概率统计得到,两者并不是同时对应的[1-2].而空调室外干、湿球温度等参数是同时作用于建筑物,并影响建筑冷负荷,因此现有的设计计算参数不合理,将给空调系统的设计和后期运行带来不利影响[3].
现阶段,我国的《民用建筑供暖通风与空气调节设计规范》GB50736-2012[9]中的夏季空调室外计算干、湿球温度,为历年平均不保证50 h的干湿球温度.该方法主要集中在单个气象参数的特征及统计规律,没有考虑两者之间的同时发生性.ASHRAE手册[10]根据不同空气参数对空气处理设备的影响,分别给出了不保证率为0.4%,1.0%和 2.0%三种水平下的室外设计干、湿球温度和露点温度,并给出了不同类型温度设计值的伴随参数.该方法本质上还是只以干球或湿球温度为主要因素,进行了一维的概率统计,并没有真正的反映干、湿球温度之间极值事件的同时发生情况.T.Y.Chen等人[13]定义了一种随建筑的热物性和室外气象参数的变化而变化的风险因子,该方法考虑了干、湿球温度之间的同时发生性,但这种方法需要结合建筑热物性不具有普遍适用性.
室外气象计算参数表征气候学意义上相对极端的气象条件,因此,研究气象参数中的近极端参数分布对室外计算参数的影响要远大于整体分布对其的影响[7].用概率论知识解释为室外干、湿球温度是同一时间维度下的两个随机变量,因此需要对两变量的二元极值分布进行研究[8-9].本文建立了干湿球温度的二元超阈值分布研究干湿球高温数据的二元联合分布,确定一种既考虑了干、湿球温度的同时发生性,也具有普遍适用性的新的计算参数的确定方法,弥补了当前确定方法上气象参数间的同时发生性考虑不足,该方法在数学意义上更合理,计算得到的室外计算干湿球温度适用于一般空调系统的设计.
1 数据来源与预处理
选择我国西北旱区代表城市乌鲁木齐进行计算.原始气象数据(乌鲁木齐市1978-01-01—2016-12-31共30 a室外干球温度及露点温度数据)由NCDC(美国国家气候数据中心)网站上下载.气象台站每日仅定时记录8次数据,将定时记录数据通过MATLAB三次样条插值[10]形成逐时数据.通过干球温度和露点温度在MATLAB上通过迭代计算获得对应的湿球温度数据.
2 现有夏季空调室外计算参数确定方法
2.1 我国夏季空调室外计算参数确定方法
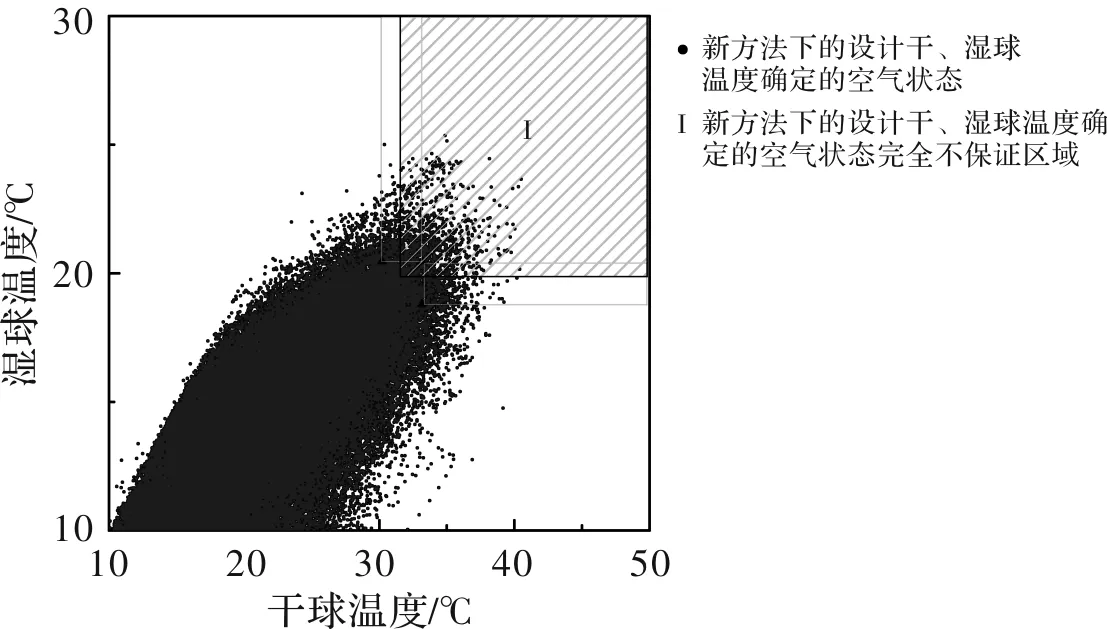
我国现行的夏季空调室外计算干、湿球温度的确定方法表述为历年平均不保证50 h的干湿球温度[4].以乌鲁木齐市为例,选取历年平均不保证时长50 h(0.57%),计算对应的室外计算干、湿球温度值,以计算得到的干、湿球温度确定其对应的实际的空气状态点,如图1所示.

图1 我国方法下得到的室外设计参数及空气状态不保证区域
按照我国方法得到的设计干、湿球温度分别为33.2 ℃,20.5 ℃,其所确定的空气状态点实际的30年的不保证小时总数为418 h,历年平均不保证约14 h,远远小于设计的不保证小时数.
2.2 ASHRAE手册夏季空调室外计算参数确定方法
美国《ASHRAE Handbook-Fundamentals》(2013版)中详细介绍了ASHRAE采用的室外空气计算参数统计方法,其中,年夏季设计参数给出了0.4%、1.0%、2.0%多种不保证率下的干球温度及对应的平均湿球温度、湿球温度及对应的平均干球温度、露点温度及对应的平均干球温度和比焓及对应的平均干球温度,并对每种类型参数的用途给出了建议[5,11].
ASHRAE中关于夏季空调室外计算参数的确定方法有以下两种:
室外设计干球温度与室外设计干球温度同时发生的湿球温度(DB,MCWB);
室外设计湿球温度与室外设计湿球温度同时发生的干球温度(MCDB,WB).
同样以乌鲁木齐市为例,选取不保证时率0.57%(50 h),ASHRAE方法确定了两组空调室外设计计算干、湿球温度.计算可得,ASHRAE以干球温度为主参数,湿球温度为伴随参数,计算得到的设计干、湿球温度为33.2 ℃,18.8 ℃.而以湿球温度为主参数,干球温度为伴随参数,计算得到的设计干、湿球温度分别为30.2 ℃,20.5 ℃.
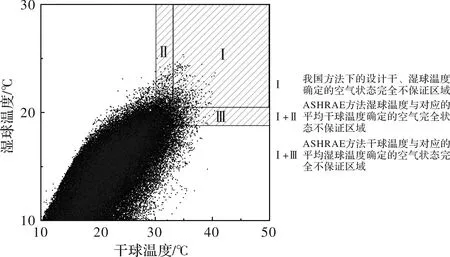
图2 ASHRAE方法下得到的室外计算参数及空气状态不保证区域
图2为ASHRAE方法下两组设计参数的的不保证区域.(MCDB,WB)确定的完全不保证区域为Ⅰ+Ⅱ,(DB,MCWB)确定的完全不保证区域为Ⅰ+Ⅲ.可以看出,ASHRAE方法下的不保证区域较我国方法下有所增加.而ASHRAE的主参数DB、WB的确定方法与我国方法相同,确定的主参数值与我国的值相同,不保证区域增加的原因是由于相应的伴随参数值MCDB、MCWB较我国方法有所降低.
表1为按照我国方法以及ASHRAE方法下乌鲁木齐市1978—2016年各参数的历年不保证时长.
从上表可以看出,按照我国方法所确定的空气状态点实际的30 a的不保证小时总数为418 h,历年平均不保证约14 h,远远小于要求的不保证50 h,说明按我国干湿球温度分别不保证50 h的确定方法所得到的干、湿球计算温度取的过于严格,这会造成不必要的浪费.ASHRAE中以干球温度为主参数,湿球温度为伴随参数所确定的空气状态点实际的30 a的不保证小时总数为938 h,历年平均不保证约31 h,而湿球温度的历年平均不保证小时数为218 h,远远高于50 h,说明设计湿球温度取得过低.而以湿球温度为主参数,干球温度为伴随参数所确定的空气状态点实际的30 a的不保证小时总数为1 025 h,历年平均不保证约34 h,而湿球温度的历年平均不保证小时数为215 h,远远高于50 h,说明设计干球温度也取得过低.
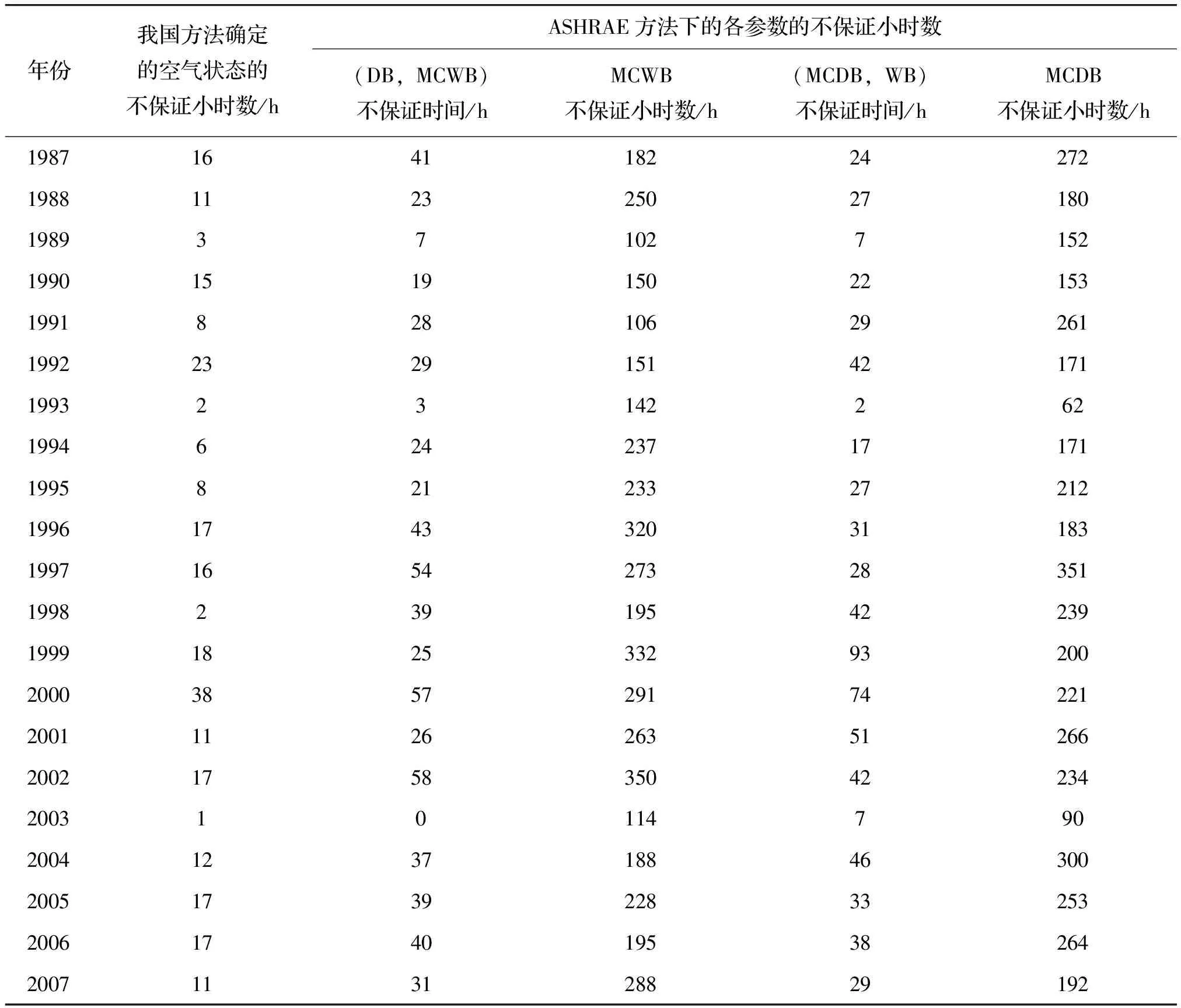
表1 乌鲁木齐市1978—2016年我国方法和ASHRAE方法下各参数不保证时长
续表1

年份我国方法确定的空气状态的不保证小时数/hASHRAE方法下的各参数的不保证小时数(DB,MCWB)不保证时间/hMCWB不保证小时数/h(MCDB,WB)不保证时间/hMCDB不保证小时数/h200818351692531420091104521542010143122035213201182512512246201256225111902013028961142014422167182612015801334241343452016193049571198平均值143121834215
3 基于二元超阈值模型完全不保证率下的空调室外计算参数确定方法
3.1 空调室外计算干、湿球温度的完全不保证率
从统计学角度来看,室外干、湿球温度是同一时间维度下的随机变量[12].2个气象参数间的同时发生性问题,即可转化为两变量之间的相关问题.由此,干、湿球温度的同时发生的问题也就可以转化为两序列的联合概率分布问题.
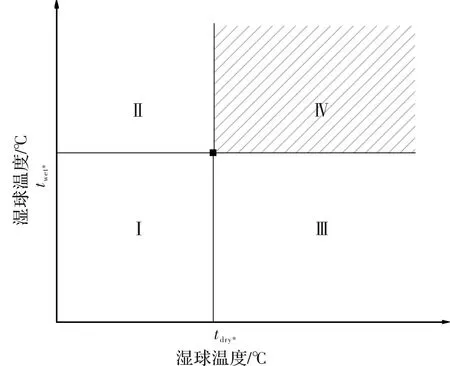
图3 同时发生的干、湿球温度划分的空气状态区域分布图
图3为同时发生的干球温度和湿球温度的确定的空气状态的区域分布图,横轴为室外干球温度,纵轴为室外湿球温度.图中的tdry*和twet*表示任何一对给定的同时发生的室外干球温度和湿球温度(即一个数据对),并且通过该给定的数据将平面划分为四个区域[10].Ⅰ区的温度分布为tdry≤tdry*,twet≤twet*;Ⅱ区的温度分布为tdry≤tdry*,twet>twet*;Ⅲ区的温度分布条件为tdry>tdry*,twet≤twet*;Ⅳ区的温度分布条件为tdry>tdry*,twet>twet*.
容易得出,与按照tdry*和twet*所计算的冷负荷相比,当tdry和twet落在Ⅰ区时,空调系统的实际负荷小于设计负荷,Ⅰ区为完全保证区域.Ⅰ区的干、湿球温度的联合频率分布为
P{Tdry≤tdry*,Twet≤twet*}
(1)
同理,Ⅱ、Ⅲ区为部分保证区域.Ⅱ区的干、湿球温度的联合频率分布可以通过以下方法得到:
P{Tdry≤tdry*,Twet>twet*}=P{Tdry≤tdry*}-
P{Tdry≤tdry*,Twet≤twet*}
(2)
右边第一项是湿球温度的边缘累积频率分布.同样,Ⅲ区的干、湿球温度的联合频率分布可以通过以下方法给出:
P{Tdry>tdry*,Twet≤twet*}=P{Twet≤twet*}-
P{Tdry≤tdry*,Twet≤twet*}
(3)
右边第一项是干球温度的边缘累积频率分布.
当tdry和twet落在区域Ⅳ时,其实际负荷大于设计负荷,这意味着一个以tdry*,twet*设计的空调系统选用的设备容量不能满足这部分区域的冷负荷.区域Ⅳ为完全不保证区域.区域Ⅳ的干、湿球温度分布的联合频率分布[12-15]可通过以下方法得到:
P{Tdry>tdry*,Twet>twet*}=
1-P{Tdry≤tdry*,Twet≤twet*}-
P{Tdry≤tdry*,Twet>twet*}-
P{Tdry>tdry*,Twet≤twet*}
(4)
Ⅳ区的联合频率分布定义为干、湿球温度的同时不保证率,联立方程式,有
P{Tdry>tdry*,Twet>twet*}=
1+P{Tdry≤tdry*,Twet≤twet*}-
P{Tdry≤tdry*}-P{Twet≤twet*}
(5)
室外气象设计参数主要表征气候学上的近极端情况,在工程设计中就以一定不保证率下,统计得到的室外温度作为设计计算温度,因此上式定义为同时发生的干、湿球温度的完全不保证率,为了解决当前确定方法干、湿球温度间同时性考虑不足的问题,确定一种基于完全不保证率的确定空调室外计算温度的新方法.
3.2 二元超阈值模型的建立
基于计算同时发生的干、湿球温度的完全不保证率过程中,涉及到干湿球温度极值间的联合分布问题,因此需要建立室外干、湿球温度间的二元极值分布,对室外气象参数建立二元超阈值模型[13].具体流程图如图4所示.建立二元超阈值模型首先研究边缘分布,再研究边缘分布间的相关性,二元超阈值模型选定阈值后,将边缘分布分成两部分,阈值以下的用经验分布拟合,再求得超过阈值的尾部边缘分布函数,通过选取合适的相关结构函数[13-14],得到二元超阈值分布,再利用极大似然估计[15-16]对参数进行估计.

图4 二元超阈值模型建立过程
3.2.1 尾部边缘分布
通过干、湿球温度的逐时高温数据的累计经验分布曲线从统计模型类中选择合适观测数的模型,拟合超过阈值的干、湿球温度的单参数尾部边缘分布.
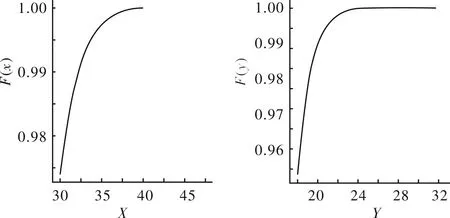
图5 乌鲁木齐市干、湿球温度的高温累计经验分布曲线
图5是干、湿球温度的高温累计经验分布曲线.由图5可以看出,干、湿球温度的高温数据的累计经验分布曲线与GPD分布[12]曲线非常相似,因此可以考虑采用GPD分布拟合超过阈值的干、湿球温度的单参数边缘分布.
对于一元分布函数F∈MDA(H),H为广义极值分布(GEV分布),F的尾部近似为广义pareto分布,对于充分大的阈值u,当x>u时,有F(x)≈G(x):
(6)
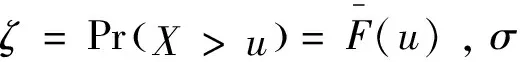
3.2.2 阈值的确定
使用阈值模型,首先要对干湿球温度两个变量分别选取合适的阈值.选取的阈值u必须足够大以保证模型的适用性,同时又必须足够小以保证有足够多的独立极值样本点来拟合模型中的参数.
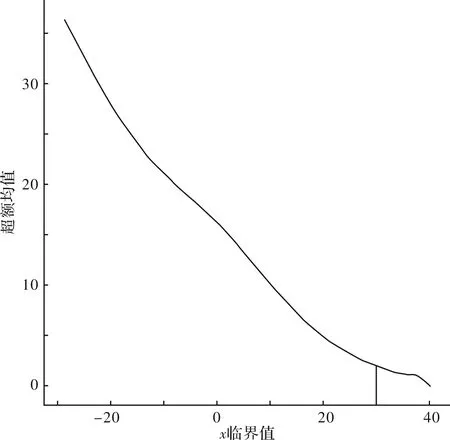
《实用极值统计方法》[13]一书中介绍了两种确定阈值的方法.在这里我们根据平均剩余寿命图来选取.平均剩余寿命图对阈值的选取是基于GPD分布的平均超出量函数.
(7)
式中,u为阈值,E(X-u|X>u)为阈值超出量的期望平均,称为平均超出量函数.当形状参数ξ稳定时,分布图近似为直线,因此可以根据平均剩余寿命图中直线段所对应的横坐标作为阈值的可选范围[13,15].
3.2.3 二元联合分布
讨论二元极值参数模型,关心的是两个极值变量间的相关关系,而这个关系由相关结构函数决定.由于相关结构函数是非参数形式,因此二元极值分布没有一般的参数形式,二元极值参数模型,主要分为logistic型与其他类型.其中logistic模型是诸多参数模型中最著名,也是实际中应用最广泛的一个模型[13,17].
作极坐标变换w=x/(x+y),通过观察w的直方图[17]来选择合适的相关结构函数.如图7所示.

图6 干、湿球温度的w值直方图
图6显示数据近似对称,Logistic 模型在实际中应用最广泛,其变量对称可交换,因此选择对称的logistic模型来描述室外空气干球温度与湿球温度,表达式为
F(x,y;α)=exp{-(x-1/α+y-1/α)α},
x>0,y>0
(8)
式中,α为拟合Logistic 模型在中的未知参数,α∈(0,1).
3.2.4 模型检验
通常用概率图(P-P图)、分位数图(Q-Q图)[17]反映观测点与二元极值模型的吻合情况.概率图(P-P图)表示了观测数据与模型吻合的情况,P-P图为
(9)
式中,Xn,n<… 对于极值模型,最关心的就是数据取大值时模型是否合适,即关心较大次序统计量的情况,此时F(Xk,n)与(n-k+1)/n+1都接近1,P-P图无法提供更详细的信息,因此更常用的是分位数(Q-Q)图: (10) 式中,F-1(x)表示F(x)的反函数,也就是分位数函数. 理论上,当X的分布函数为F(x)时,P-P图和Q-Q图应近似为直线. 利用R软件中的mrl.plot函数[13]可以得到室外空气干球温度与湿球温度的平均剩余寿命图,见图7,从图中可以看出,在ux为30,uy为18附近时,图形的斜率近似为直线,由于选取的阈值u必须足够大以保证模型的适用性,同时又必须足够小以保证有足够多的独立极值样本点来拟合模型中的参数.因此取阈值ux=30,uy=18较合理. 图7 室外干球温度与湿球温度的平均剩余寿命图 可以看出GPD模型中含有两个参数,logistic模型含有一个参数,利用R软件中的fbvpot函数可得到二元超阈值模型中未知参数的最优估计[18].计算得到的二元超阈值模型结果为 x>30,y>18 (11) 其中边缘分布为 x>30 (12) y>18 (13) 图8是干、湿球温度的P-P图和Q-Q图,由图可见,观测点与广义极值分布模型拟合良好,故可作为二元极值模型的边缘分布样本. 图8 P-P图和Q-Q图 利用二元超阈值分布计算空气状态不保证率分别为0.57%(不保证小时数50 h)时对应的计算干、湿球温度值,并与我国方法及ASHRAE方法对应值比较基础数据为乌鲁木齐市1978-01-01—2016-12-31共30年室外逐时干湿球温度.结果如下表所示. 表2 三种方法确定的干、湿球温度值比较 ℃ 图9 新方法下得到的室外计算参数及空气状态不保证区域 图9给出了我国方法、ASHRAE方法以及二元超阈值方法这三种夏季空调计算参数确定方法计算得出的空调室外计算干、湿球温度以及实际空气状态点完全不保证区域.按新方法计算得到的设计干球温度为31.6 ℃,设计湿球温度为19.9 ℃,设计干球温度的实际历年平均不保证时长为113 h,设计湿球温度的实际不保证时长为90 h.设计干、湿球温度对应的实际空气状态点的历年平均不保证时长为32 h.由于同时考虑了干、湿球温度的不保证水平,因此按照新方法计算得到的设计干、湿球温度值较我国方法有所下降,其中空调室外计算干球温度降低约1.6 ℃,空调室外计算湿球温度降低约0.6 ℃.与ASHRAE方法中湿球温度为副参数时比较时,空调室外计算湿球温度升高约1.1 ℃,与ASHRAE方法中干球温度为副参数时,空调室外计算干球温度升高约2 ℃.从统计学角度出发,对干、湿球温度建立的二元超阈值模型,同时考虑了干、湿球温度的极值同时发生的情况,相较我国方法与ASHRAE方法更加合理. 针对当前夏季空调系统的设计计算干湿球温度空调室外设计计算干、湿球温度的确定方法主要集中在单个气象参数的一维概率统计,而两者之间的同时发生性考虑不足的问题,提出当实际空气状态点的干、湿球温度都大于设计计算温度时,这部分的空气状态点位于完全不保证区域的概念,为建立二元超阈值模型并计算在一定不保证率下同时发生的设计计算干、湿球温度提供基础.主要结论如下: 1.对于超过一定阈值的干、湿球温度数据总体服从广义帕累托分布(GPD),且干湿球温度间存在较强的相关性,对这两变量的二元极值分布进行研究,可以找到合适的二元相关结构函数建立二元超阈值模型研究这两个参数的高温数据之间的二元极值分布. 2.我国方法以乌鲁木齐为例进行案例分析,在同时不保证率0.57%(50 h)的新方法下求得的空调室外设计干湿球温度相对于我国方法,干湿球温度分别下降了1.6 ℃,0.6 ℃. 3.新方法下求得的空调室外设计干湿球温度相对于ASHRAE方法中MCWB,湿球温度升高约1.1 ℃,相对于MCDB,干球温度升高约2 ℃.相比ASHRAE方法只以干球或湿球温度为主要因素,进行一维的概率统计的方法,在数学意义上更为合理. 新方法考虑气象参数极值间的同时发生性,对现在仅以单参数不保证率的确定方法进行了改进,为空调系统的设计计算参数提供了一种更为科学合理的确定方法.4 结果与分析
4.1 二元超阈值模型的建立及模型检验

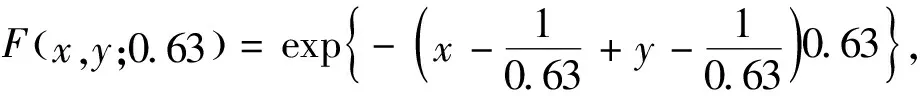

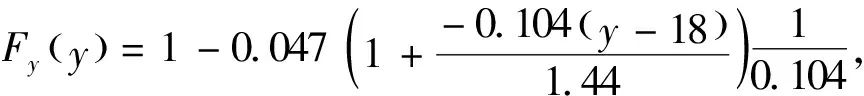
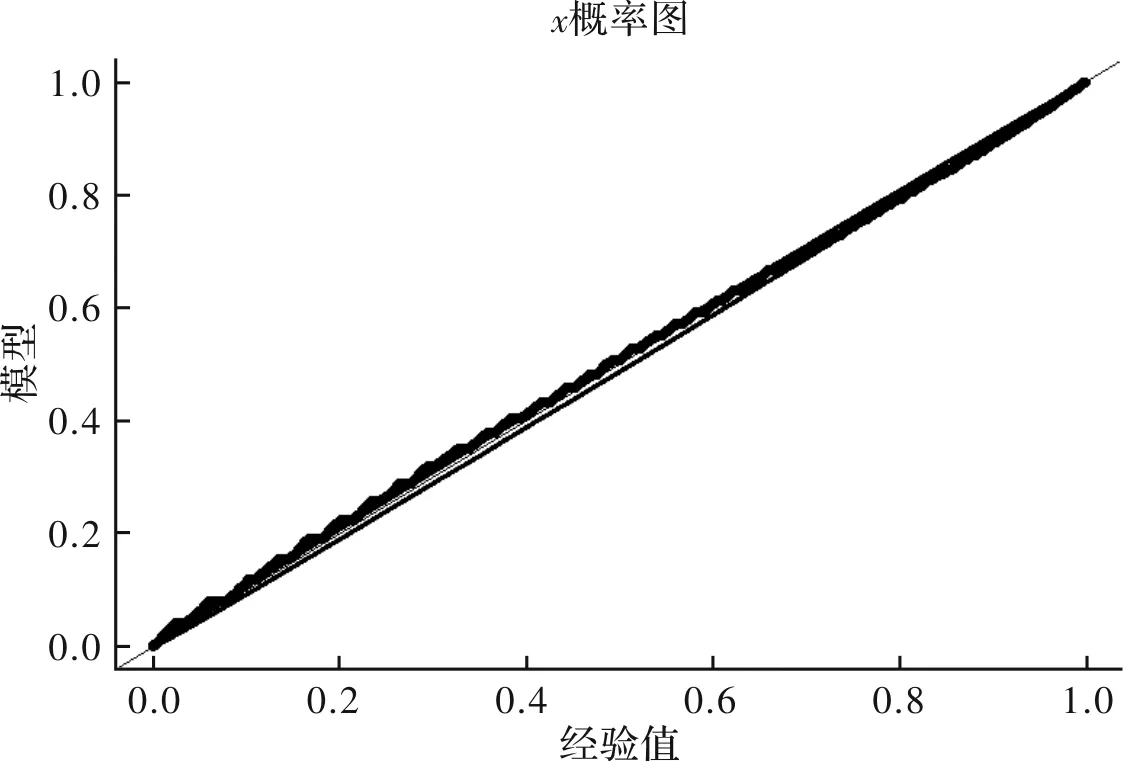
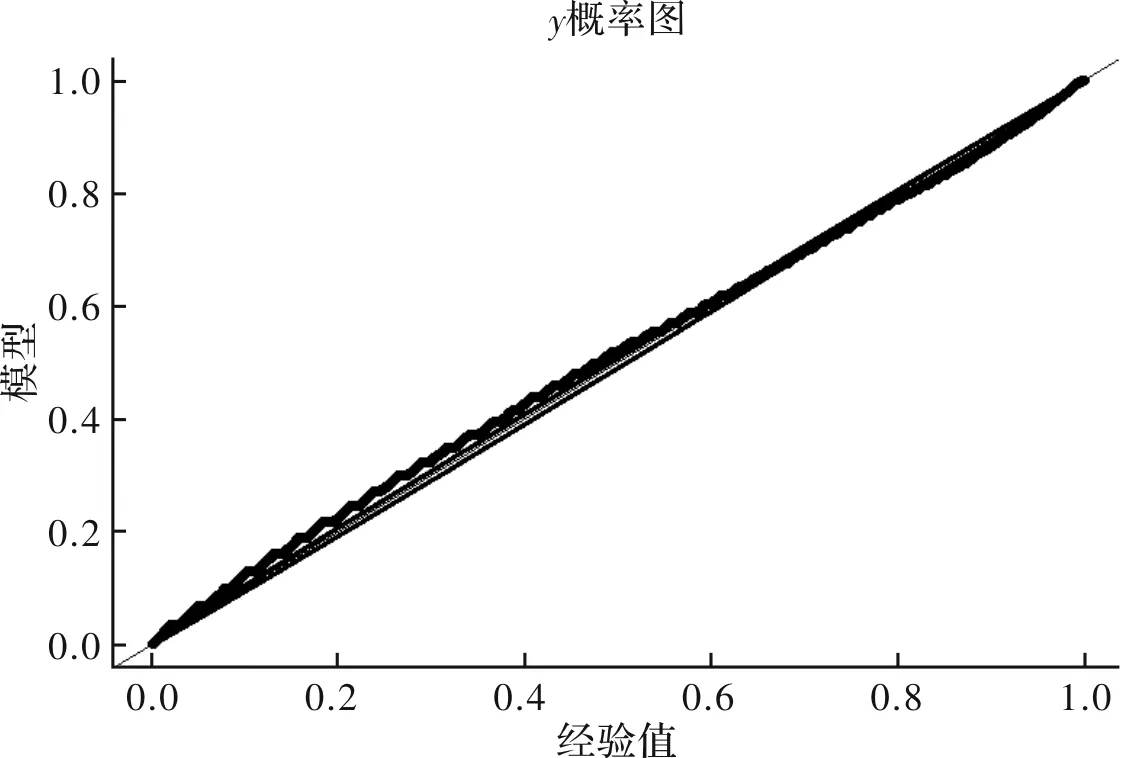


4.2 同时发生的空调室外计算干、湿球温度

5 结论

