靠近迭代法获取湿球温度初探
刘银秀 熊守权
(1 湖北省气象信息与技术保障中心,武汉 430074;2 湖北省气象服务中心,武汉 430205)
0 引言
湿球温度是表征大气物理状态的一个要素。是气象台站曾经的最基本测定项目之一。进入21世纪后,由于我国地面气象观测系统的自动化,相对湿度值由仪器自动测定,各气象台站基本停止了湿球温度要素观测,但在实际气象服务中,有时还要用到湿球温度:如核电厂冷却塔设计中,确定最终热阱系统的容量时,必须规定设计基准气象参数,首先确认了内陆核电站最终热阱关键气象参数之一为空气湿球温度[1];再如大容量火电机组凉水塔效率的计算[2];还有湿热地区城市热环境评价[3]等。如何获取新时期湿球温度的历史资料,不少学者进行了诸多探索。王海军[4]为解决无湿球温度资料给工程设计带来的问题,分别设计了逼近法(实际上就是迭代法)和多元回归法估计湿球温度,指出采用逼近法估计湿球温度误差很小;湿球结冰对湿球温度的估计影响不大。目前国内很多学者多以气象学公式为基础,运用迭代法来完成湿球温度的插补[5-8]。朱业玉等[9]根据气压分布型特点和分段函数,提出利用干球温度和相对湿度来计算湿球温度的新方法。
魏华兵等[6]利用湿球温度的经验公式计算初始值,采用Execl电子表格完成湿球温度的迭代计算自动气象站湿球温度,并指出“迭代法进行推算时,要先给迭代变量赋予一个初始值,而初始值的选用对迭代过程的计算至关重要”。并根据指定气象站实测的气温和相对湿度资料用泰勒多项展开式对参数进行求算初始值,其初始值结果是“只有在气温为10~20℃,相对湿度为80%~90%时,计算误差稳定,而其他情况下,误差很不稳定,误差有时超过10%”。另外,其初始值资料不具备普适性。
朱业玉等[9]、魏华兵[6]在湿球温度求算过程中均使用了相对湿度。在《湿球温度查算表(甲种本)》中,相对湿度的分布情况比较宽泛:在气温相同的情况下,一个相对湿度可以对应3~6个湿球温度值。如t=48 ℃,U=1%时,对应了6个湿球温度值;t=45 ℃,U=15%时,对应了4个湿球温度值;t=36 ℃,U=13%时,对应了3个湿球温度值。程智等[5]指出,“从干球温度以下15℃的范围内选取湿球温度的估计值,每次将湿球温度估计值递增0.01 ℃(根据实际经验,15 ℃的范围是足够宽的),因此可以得到m+1个估计值”迭代次数1500次。
在实际气象资料服务中,作者感觉上述方法实现起来不够简捷,试图利用湖北省70多个站的近50万条包含湿球温度的历史记录,通过SQL Server数据库查询手段,采用气温、水汽压相等或约等的方法,对近年的资料进行关联查询获取湿球温度,以满足客户所需。但出现了要么找不到匹配值,要么找到了多个相互差异较大的值。受人工从《湿球温度查算表(甲种本)》中反查湿球温度过程的启发,盟生了建立“小型湿度查算表”,以水汽压不变、气温逼近的原理进行迭代计算的思路。
1 资料来源与方法
本文使用实际观测数据作为测试数据,为湖北气象档案室提供的区站号57476、57482两个站1981—1991年5—9月的定时观测数据,含定时气温、定时水汽压、定时相对湿度、定时气压、定时湿球温度等多个要素,共计11780条实测记录(剔除不明记录后)。
1.1 基本原理
《湿度查算表(甲种本)》中,湿度查算表是以戈夫-格雷奇(Goff-Gratch)公式为基础编制的。考虑到实际应用,如核电厂冷却塔设计中,所需资料均是相对高温的情况,故本文只进行了湿球未结冰(纯水面)状态下湿球温度的计算方法探讨。
(Goff-Gratch)公式中,纯水面饱和水汽压
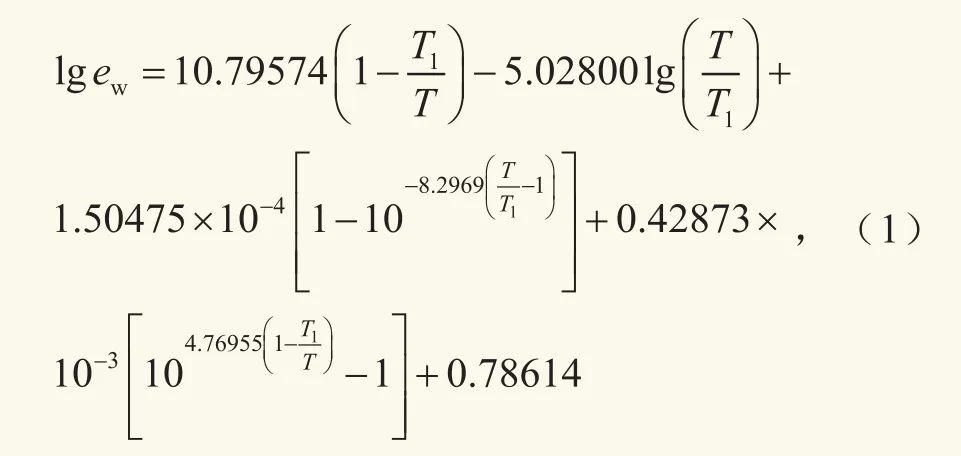
式中,纯水面饱和水汽压ew(单位:hPa,温度范围:-49.9~49.9 ℃);T1=273.16 K(水的三相点温度);T(K)=273.15+t ℃(绝对温度)。
干、湿球温度求空气中水汽压的计算公式

t为干球温度,tw为湿球温度,单位℃;为湿球温度tw所对应的纯水面饱和水汽压,A为干湿表系数。
湿度查算表中,取P=1000 hPa;在湿球未结冰时,A=0.667×10-3(℃-1)
由式(2)推导


另外,《湿球温度查算表(甲种本)》湿球温度气压订正值Δtw(℃)的公式为

P为实测本站气压;P0=1000 hPa;A的意义和取值同上,百叶箱通风干湿表A=Ai。
1.2 靠近迭代法实现步骤
靠近迭代法实现中,主要借助了SQL Server数据库、VBA两个工具。
首先需要建立一个纯水面饱和水汽压函数。利用式(1),通过自变量气温t可以直接获取对应的纯水面饱和水汽压ew。湿球温度tw所对应的纯水面饱和水汽压etw需要也通过此函数获得;其次建立小型湿度查算表:应用饱和水汽压函数和上述原理,构建从0~48 ℃,步长为3 ℃的小型湿度查算表(下称“小型湿度查算表”,示例见表1)。共包含0 ℃、3 ℃、6 ℃、9 ℃……直到39 ℃、42 ℃、45 ℃、48 ℃共17个气温对应的湿度查算表,总计2844条记录。每条记录含5个字段:t、tw、U、e、n分别表示气温(干球温度)、湿球温度、相对湿度、水汽压、对湿球温度进行气压订正时的订正参数。
被计算对象(实际观测数据)的对应数据入库,含区站号、时间、t1、p1、e1等信息;在入库时,要加上一个“序号”字段,为后期的各项处理,提供一个纽带。先用结构查询语言联表查询,查询条件为|e1-e|≤0.2,|t1-t|≥-3和|t1-t|≤10,然后对查询结果进行迭代。
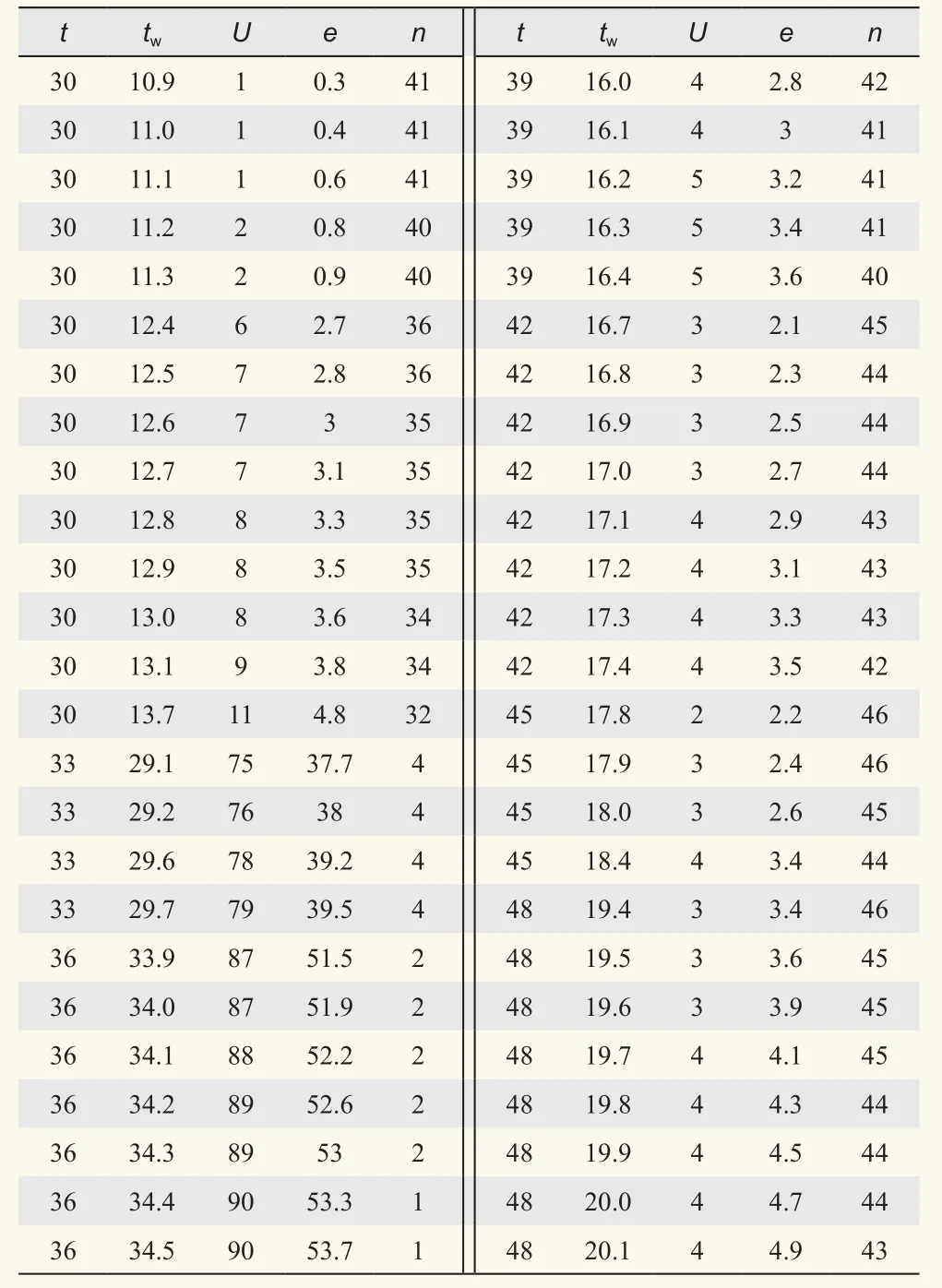
表1 小型湿度查算表示例Table 1 Example of a small humidity checklist
1.2.1 靠近迭代法整个流程变量说明
t、e、tw分别为从“小型湿度查算表”获取的气温、水汽压及对应的湿球温度;t1、e1、tw1分别为观测值气温、水汽压及对应的需要求取的湿球温度;t′、t′w分别为迭代时的临时气温值、迭代时的临时湿球温度,二者均随迭代的推进持续变化。Δtw=±0.1,为t′w的迭代步长。dif_t=|t1-t′|为迭代时的临时气温值与观测值气温的差值绝对值,是控制迭代终点的关键变量。k代表迭代次数。
1.2.2 迭代方法与经验
靠近迭代法是指利用式(4),以t所对应的湿球温度tw为基础,当t1<t时,Δtw=-0.1,称为负向迭代;反之,当t1>t时,Δtw=0.1,称为正向迭代。在正常迭代过程中,dif_t会渐渐由大变小,到达谷点(通常低于0.5)以后,再开始渐渐由小变大(见图1)。dif_t的谷点,所对应的临时t′w便是迭代所求的湿球温度。
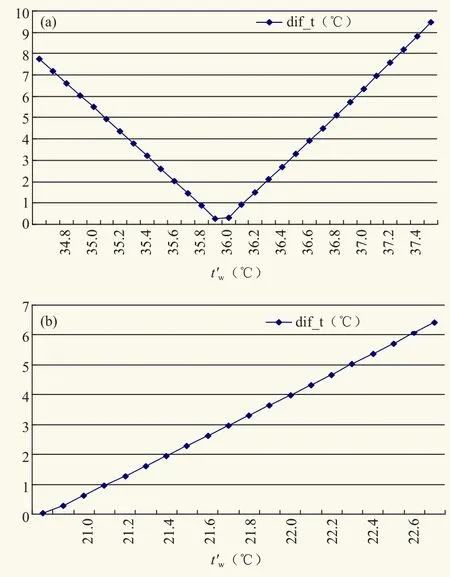
图1 dif_t随t′w的变化图Fig. 1 The change of dif_t with t′w
图1a为t=40,e=51.6,tw=34.7,t1=48 时,dif_t随t′w的变化图。图中,谷点tw1=36.0,dif_t=0.278427。
根据作者迭代经验,运用本迭代法时需要注意如下几点:
1)迭代起点为t′w=tw。当dif_t单调上升时,tw1会在起点。例如图1b:t=24,e=22.6,tw=20.9,t1=24.1时,tw1=20.9。
2)取迭代结果时,需满足tw1<t1。
3)迭代次数的上限设为100次足以满足迭代需求。
4)dif_t的谷点上限值设为0.5 ℃。
2 结果与分析
作者共进行了两种数据测试:在实际观测数据测试的基础上,为了考察靠近迭代法在各个数据段湿球温度结果的准确度,又进行了典型数据测试。
2.1 实际观测数据测试
选取江汉平原西部荆州和北部的孝感(区站号分别为57476、57482)两个站1981—1991年5—9月的定时观测数据,含定时气温、定时水汽压、定时相对湿度、定时气压、定时湿球温度等多个要素,共计11780条实测记录(剔除不明记录后)。通过与“小型湿度查算表”联合查询共查出60838条记录。实测记录每条对应1~21条查询结果(表2)。

表2 实测记录数对应查询结果数分布情况表(单位:条)Table 2 The number of measured records corresponding to the distribution of query results (unit: record)
60838条记录迭代次数分布情况:迭代次数出现次数最少1次,最多52次,87.2%的记录迭代次数在15次以内;92.9%的记录迭代次数在20次以内;98.5%的记录迭代次数在30次以内;迭代次数在35次以上的只有0.5%的记录。
设t′w1为测试对象历史资料中已有的与t1、e1对应的湿球温度。t′w1为t1、e1人工查算纸质《湿球温度查算表(甲种本)》得到的湿球温度。
计算湿球温度结果与实际观测结果的差值绝对值,共有53416条记录(占总数的87.8%)|t′w1-tw1|≤0.2,共有57277条记录(占总数的94%)|t′w1-tw1|≤0.3。对剩余的3561条|t′w1-tw1|>0.3的记录,在《湿球温度查算表(甲种本)》中,逐条通过实测气温、实测水汽压反查湿球温度:求算湿球温度结果与反查结果的差值绝对值,3373条|t′w1-tw1|≤0.1,只有186条|t′w1-tw1|=0.2。
因此,求算湿球温度结果与实际观测结果的差值绝对值均≤0.3,其中共有56977条记录(占总数93.7%)≤0.2。因此,当一条实测记录对应多条查询结果时,选取其中任一条结果均是可行的。
2.2 典型数据测试
选择0、5、10、15、20、25、30、35、40、45 ℃共10个t值,每个t值对应5个相对湿度值,U值分别为10%(或者5%)、30%、50%、70%、95%,合计50条记录。计算50条记录各自对应的e值,通过查《湿度查算表(甲种本)》获取相应的tw值。
50条记录,每条分别人为相应设置2组t1,e1值(|e1-e|=0.2),整个典型数据测试共100条数据:一组t1<t,另一组t1>t,两组中|t1-t|接近5 ℃。当t1<t时,二者差距要小一点。因为差距大了会超出极限情况:如t=0,e=5.8,取t1=-0.3。若t1=-3,对应的饱和水汽压仅为4.9,以上数值为基础负向迭代时,e=5.8就超出了极限,这种情况在实际中基本不会出现。迭代结果见表3(因表格太大,省略了5、15、25、30、35、45 ℃等t值)。
设t′w0为t1、e人工查算纸质《湿球温度查算表(甲种本)》得到的湿球温度,t′w1为t1、e1人工查算纸质《湿球温度查算表(甲种本)》得到的湿球温度。
从表3可见,最大迭代次数<30;|t′w0-tw1|≤0.1,其中96%的结果为0.0,表明迭代法的迭代精度在0.1以内;|t′w1-tw1|≤0.2,其中18%的结果为0.2,误差稍大,如果通过后文所述e-e1的水汽压差值订正,湿球温度订正后的误差均在0.1以内。
2.3 相关问题分析
2.3.1 水汽压相差0.2对湿球温度的影响
选取气温为0 ℃、6 ℃、12 ℃、21 ℃、30 ℃、45 ℃,相对湿度为5%、50%、95%时,从“小型湿度查算表”查询统计湿球温度每增加0.1 ℃时水汽压的变化值。
从表4可见,高温高湿的条件下,水汽压随湿球温度的变化大。在气温≤30 ℃,无论相对湿度多少(或者温度低于36 ℃,且相对湿度低于50%)的前提条件下,当Δe=e-e1=0.2时,如果对迭代的湿球温度结果减去0.1;当Δe=e-e1=-0.2时,如果对迭代的湿球温度结果加上0.1,湿球温度结果将更精确。一般湿度情况下,气温高于30 ℃时,水汽压的变化值0.2 hPa对湿球温度的精度影响在0.1 ℃以内,即使不结合e-e1,对迭代的湿球温度进行上述订正,所得湿球温度的误差≤0.2。
典型数据测试中,通过e-e1的水汽压差值对湿球温度tw1结果订正,订正后的湿球温度与查《湿球温度查算表(甲种本)》的结果相差均在0.1以内(表3)。
实际观测数据测试中186条|t′w1-tw1|=0.2的记录,对应实测气温为15~30 ℃,其中的182条Δe=0.2或Δe=-0.2,按上述规则进行了0.1 ℃的湿球温度tw1结果订正,进一步地提高了湿球温度求算结果的精度。
2.3.2 关于气压订正
整理式(5)得
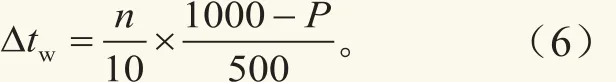
因为n>0,故|Δtw|与|1000-P|成正比。当n一定时,|1000-P|越大,|Δtw|越大。|Δtw|与|1000-P|同号:当P>1000时,Δtw<0;当P<1000时,Δtw>0。利用式(6)计算,得湿球未结冰时的“百叶箱通风干湿表湿球温度气压订正值表”(表5)。
湖北省非山区站,全年极端最高气压约为1040 hPa,极端最低气压约为980 hPa,最小相对湿度一般大于10%。当相对湿度>10%时,利用“小型湿度查算表”查询,n值的最大值为34。从表5中可知,不进行气压订正,靠近迭代法所求湿球温度的误差绝对值不超过0.2 ℃。
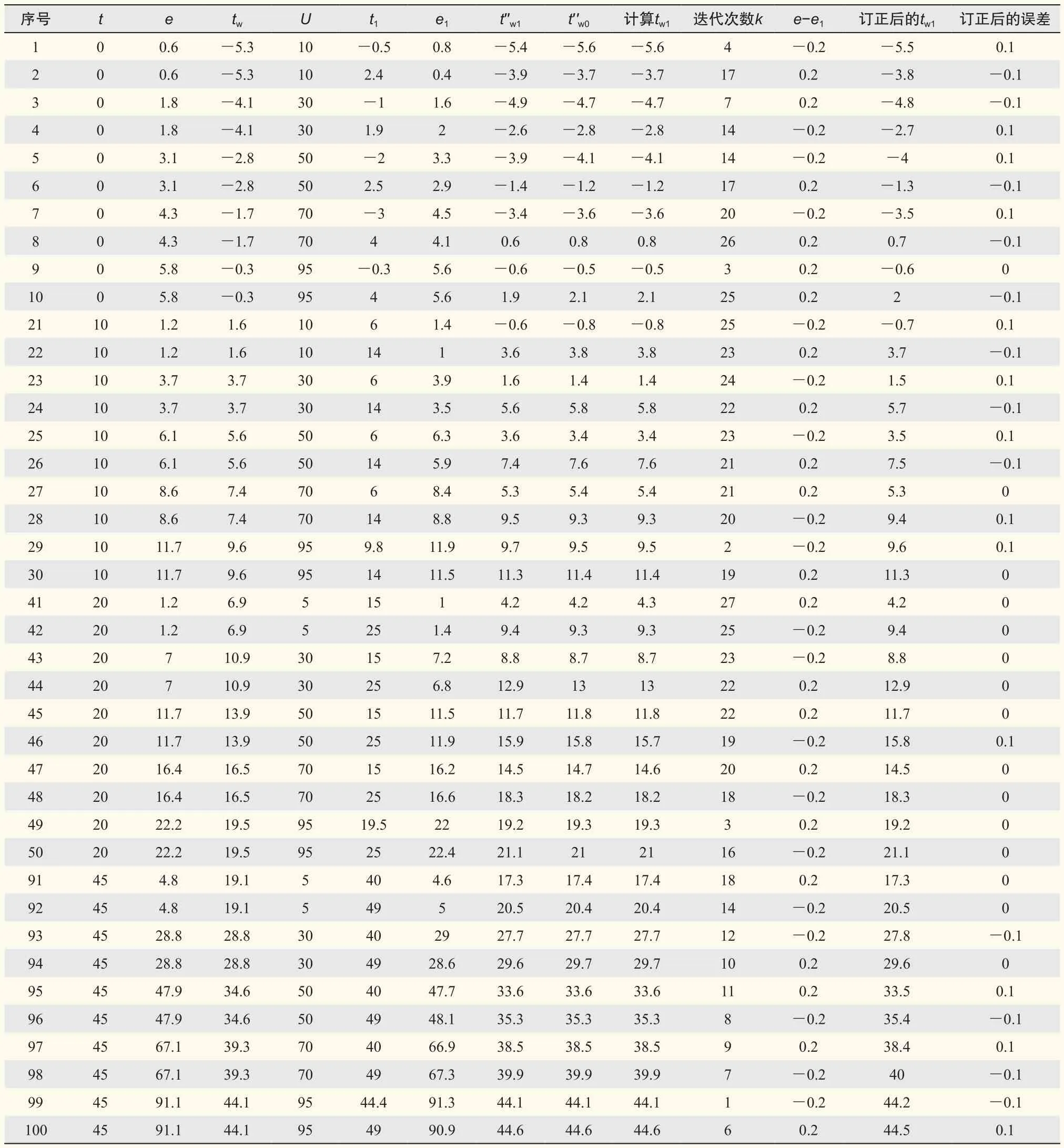
表3 不同温湿度段典型个例迭代情况表Table 3 Typical case of iterations of at different temperature and humidity sections
对于特殊条件下,有特殊需求时,亦可依据表5对tw1进行n值订正。
3 结论与讨论
本文探讨了气温在-5~49.9 ℃,水汽压已知,湿球未结冰条件下的自动气象站湿球温度求算方法。以建立饱和水汽压函数为基础,构建了步长为3 ℃的“小型湿度查算表”,是解决湿球温度迭代计算初始值难题的新尝试;经人工抽查校对,“小型湿度查算表”与《湿球温度查算表(甲种本)》相关内容几乎完全一致,更符合传统的气象标准;王海军、魏华兵、程智均是以气温不变,水汽压逼近的原理进行迭代计算的,而本文中靠近迭代法,是以水汽压不变,气温逼近的原理进行迭代计算,是不同于众学者方法的一种新的尝试;迭代过程试验最大值52次,控制在100次以内即可,节省了迭代时间。
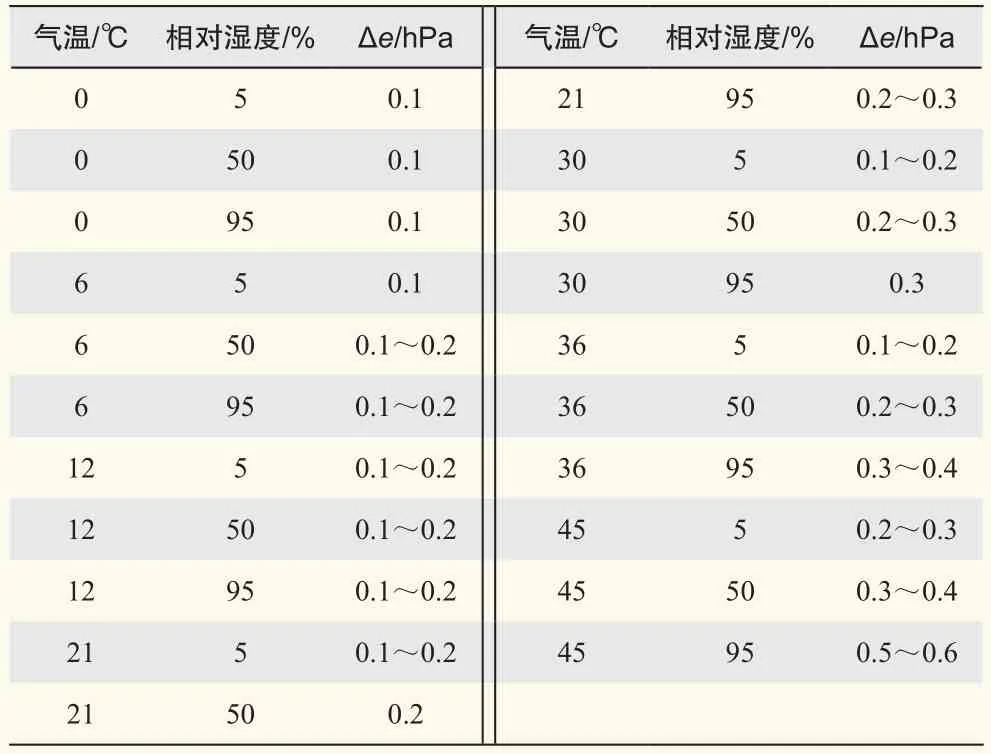
表4 不同温湿条件下Δtw=0.1时Δe值表Table 4 Δe value for different temperature and humidity(Δtw=0.1)
典型数据测试所得湿球温度与查《湿球温度查算表(甲种本)》的结果误差均在0.1或以内;历史数据测试误差93.7%在0.2或以内,所有误差在0.3或以内(其中不排除历史资料自身问题)。靠近查询、迭代求算获取自动气象站湿球温度的方法测试效果良好。
如果想进一步提高计算精度,不妨建立步长为2℃甚至1 ℃的小型湿度查算表,其记录数在10000条以内。用以上思路,得到小时甚至分钟的湿球温度记录也很容易。如因特殊需求,湿球结冰条件下的的湿球温度求算方法也可以依本文思路进行探求。
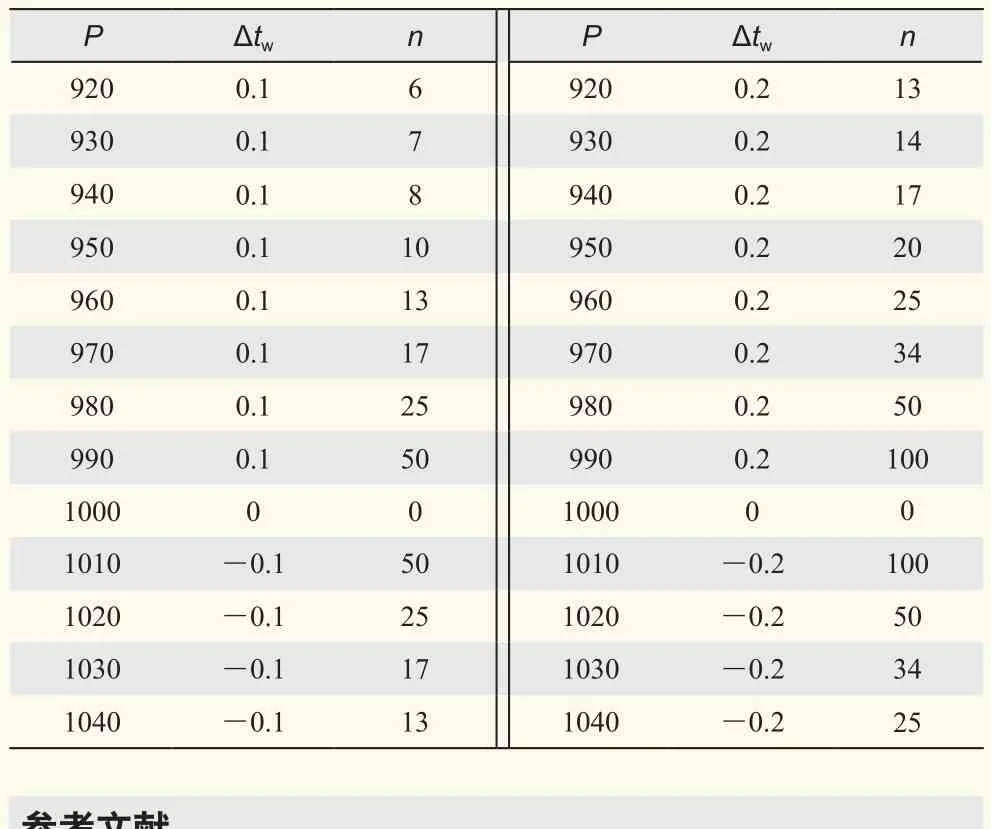
表5 百叶箱通风干湿表湿球温度气压订正值表Table 5 Corrected value of air pressure from louver box ventilation dry and wet table wet bulb temperature
 Advances in Meteorological Science and Technology2019年2期
Advances in Meteorological Science and Technology2019年2期
- Advances in Meteorological Science and Technology的其它文章
- 媒体扫描
- 新书架
- 甘肃省风能太阳能气象服务业务平台开发及应用
- 实际环境下光储离网型发电系统优化设计研究
- 中关村高企协气象科技专业委员会正式运行
- 辽宁省追踪式与最佳倾角斜面总辐射的推算与分析
