敷设空腔尖劈的声呐平台声学特性研究*

姚熊亮 计 方

(哈尔滨工程大学船舶工程学院 哈尔滨 150001)

敷设空腔尖劈的声呐平台声学特性研究*

姚熊亮 计 方

(哈尔滨工程大学船舶工程学院 哈尔滨 150001)

声呐平台;空腔尖劈;敷设方案;自噪声

基于变截面波导理论建立吸声系数方程,讨论了不同静压下尖劈吸声性能,开展了空腔尖劈声管测试,并将计算值与实验值进行对比分析。在此基础上,通过数值试验预报了声呐平台区的自噪声分布,对比分析了空腔尖劈敷设方案对其声学特性的影响。结果表明:随着静水压力的增大,尖劈吸声系数第一谐振峰向高频移动;高静压下,尖劈吸声系数下降较快。敷设空腔尖劈的声呐平台区的自噪声总声压级显著降低,尖劈部分优化敷设既要考虑全频段平台区的自噪声总声级,又要兼顾声呐基阵位置处的声压分布。

0 引 言

声呐性能的发挥不仅受基阵及导流罩功能的影响,还与声呐平台区自噪声的大小密切相关,平台区自噪声1 kHz降低3 dB,则本艇声呐的探测距离可增加30%[1]。空腔尖劈具有阻抗逐渐过渡的性质,在较宽的频带内具有优良的吸声性能。将其敷设于声呐平台区的后壁板以及将声呐平台区和上层建筑艏部分开的水平平台,可以有效降低声呐平台区自噪声,具有较强的工程应用价值。

文献[2]应用统计能量法预报了潜艇艏部平台的自噪声并进行了模型试验;文献[3]阐述了船舶声呐部位自噪声的产生机理及其控制技术,但并未涉及尖劈结构在声呐区的应用;文献[4]把尖劈材料和传声媒质的声学参数按面积做计权平均得到等效参数,按照平板型吸声结构的相应理论计算其吸声性能;文献[5]类比变截面管中的声传播特性,应用变截面波动方程建立了尖劈吸声系数计算方程,但并未研究静水压力对空腔尖劈吸声性能的影响。本文在上述文献的基础上,依据变截面波导理论建立吸声系数方程,讨论了不同静水压力下尖劈吸声性能,并将计算值与实验测试结果进行了对比。以空腔尖劈材料力学参数及吸声性能测试数据作为输入,通过数值试验研究了敷设空腔尖劈的声呐平台区的声学特性,对比分析了空腔尖劈敷设方式对平台区声学特性的影响,所得结论对舰艇艏部声呐平台区的声学设计以及尖劈材料配方优化具有一定的参考意义。

1 声呐平台区声自噪声特性分析

舰艇艏部声呐平台区主要由上、下平台,后壁,基阵支撑筒和导流罩组成,如图1所示。

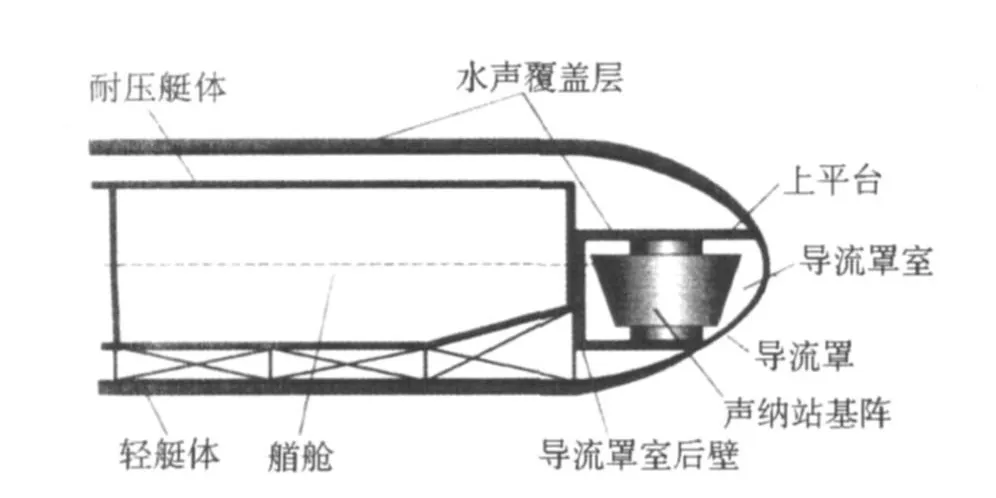
图1 敷设尖劈的声呐平台区示意图

舰艇声呐平台区总的声干扰取决于其所有水声分量的能量和为[6]:

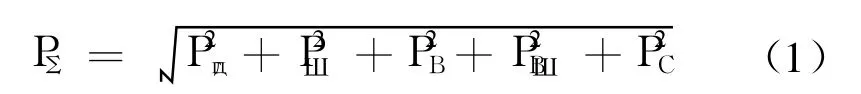
式中各干扰量分别为:水动力紊流干扰分量Pгд,水噪声干扰分量PШ,振动干扰分量PВ,设备空气噪声的干扰分量PВШ,结构干扰分量PC。由总干扰公式可见,个别分量级减少一定值,并不引起总干扰减少相应的值。

声呐平台区受简谐激励产生稳态动响应的同时,诱发结构噪声并向周围介质辐射,其辐射声功率为:

式中:ρ为介质密度;c为介质声速;s为辐射面的面积;σrad为辐射系数为辐射面振动的均方速度。式(2)经过运算后可得到辐射声压的表达式:

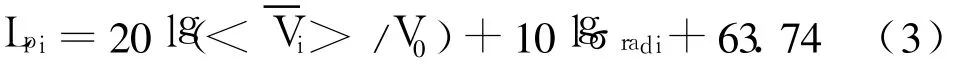
式中:均方速度基准值为V0=1.0×10-9m/s;和σradi分别为各辐射面的振动均方速度和辐射系数。

为了降低声呐腔内自噪声量级,声腔内部分钢结构表面敷设空腔吸声尖劈进行降噪处理,此时声腔内的自噪声是计及声学材料的减振和吸声性能。则式(3)变为[7]:

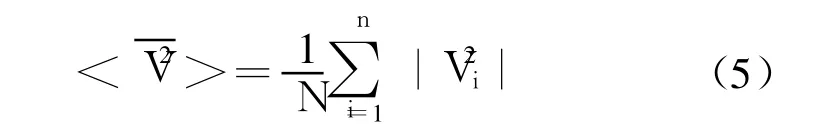
A为声腔内总吸声量

式中,Si和αi各为辐射面面积和敷设相应材料的吸声系数。求得各部分辐射噪声的声压级后,再进行合成,就可得到声腔内的总声压级为:

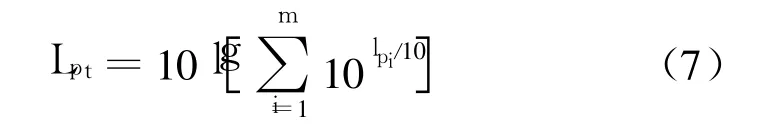
结构辐射系数σradi表示结构声辐射的能力,它与结构形式、尺寸大小和振动频率有关。σradi根据结构特点采用经验公式求取。其具体计算方法如下:

式中,σradi是第i部分结构的辐射阻。

由于声腔各部分结构的形式特征不同,计算辐射系数的方法也各不相同。根据实际声呐腔结构,上平台、下平台、后壁和导流罩按四边简支板架计算辐射阻,再按式(8)计算辐射系数,圆筒按圆柱壳计算声辐射系数。

2 空腔尖劈吸声性能计算及测试

2.1 尖劈吸声性能计算

本文应用变截面波导理论、对尖劈结构进行分层处理。设空腔尖劈为弹性媒质,不考虑空腔内充空气的切变应力,平面声波以垂直于尖劈横截面的方向入射到尖劈顶端和侧面,将尖劈等分成n个环形台面,S0,S1,S2,…,Sn分别为尖劈的底、环面和顶端的面积。

图2 尖劈分层处理示意图

入射到尖劈顶端和侧面的声波总能量可表示为:

其中Ii为声强。设IrjSj为尖劈第j个环形面上的声波反射能量,则总的反射能量和吸收能量分别为:

定义第Sj面的声强反射系数为:rj=Irj/Ii,则尖劈的吸声系数为:

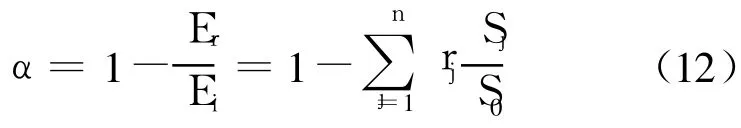
尖劈吸声结构的内截面(空腔)和围壁(吸声材料)的截面积沿对称轴x轴变化,则尖劈吸声结构的特性阻抗率ρc/S(x)是x的函数。假定其中传播的声波波阵面按截面的规律变化,则对应的声场应满足变截面形式的波动方程[5],这样带空腔尖劈吸声结构顶端和各环形面的声强反射系数rj可用变截面波导的声场理论计算:

第j个截面总的输入阻抗ZAi可以由变截面波导理论得出:

式(14)具体推导过程及式中参数含义见文献[10]。由反射系数与输入阻抗关系式求得声强反射系数rj,最后得到尖劈吸声结构的吸声系数α表达式如下:

式中ZAm是尖劈顶端输入声阻抗

其中ρwcw为入射声波所在介质的特性阻抗。

在静水压力作用下,空腔会产生径向和轴向变形,会使截面积发生变化,而轴向变形也会使尖劈的长度产生相应的变化,进而影响尖劈的吸声性能。尖劈材料密度变化不大,所以密度变化这里暂且忽略。在满足材料强度等因素要求的情况下,尖劈的吸声系数仍可以用前述分层介质变截面波导计算。本文采用有限元法计算尖劈在静水压力作用下的变形,假设应力—应变关系为线性[11],首先获得尖劈内部腔体和外部结构的几何变形数据,然后根据这些数据重新建立吸声系数的计算方程,计算其吸声性能。

2.2 空腔尖劈吸声性能测试

利用水声无源材料声脉冲管数字测试系统,对含有空腔的尖劈样品的法向声吸收特性进行测量。该系统主要用于水声材料样品在声软末端或声硬末端情况下复反射系数的测量,根据复反射系数的测量结果计算试样的吸声系数、输入阻抗、纵波声速和衰减、弹性模量等。声脉冲管法的数字测试系统组成示意图如图3所示。收发换能器位于声管的一端,向声管中发射脉冲调制的正弦波,经声管中的试样反射,再由同一换能器接收反射声波,系统的信噪比应该不小于20 dB。通过与柔性标准反射体反射波声压幅值和相位的相对比较,测量试样复反射系数的幅值和相位,进而通过计算得到试样的吸声系数等其他声学参数。

图5给出了不同静压下空腔尖劈吸声系数的计算值。可以看出,随着静水压力的增高,吸声系数曲线形状基本不变,但第一谐振峰向高频移动,这主要是由于在静水压力作用下空腔的有效容积变小、内径变细引起的;而高频段,吸声系数略有下降。图6为不同静压下尖劈样品吸声系数的实测值。可以看出,高静压下,整条曲线的吸声系数下降更快。

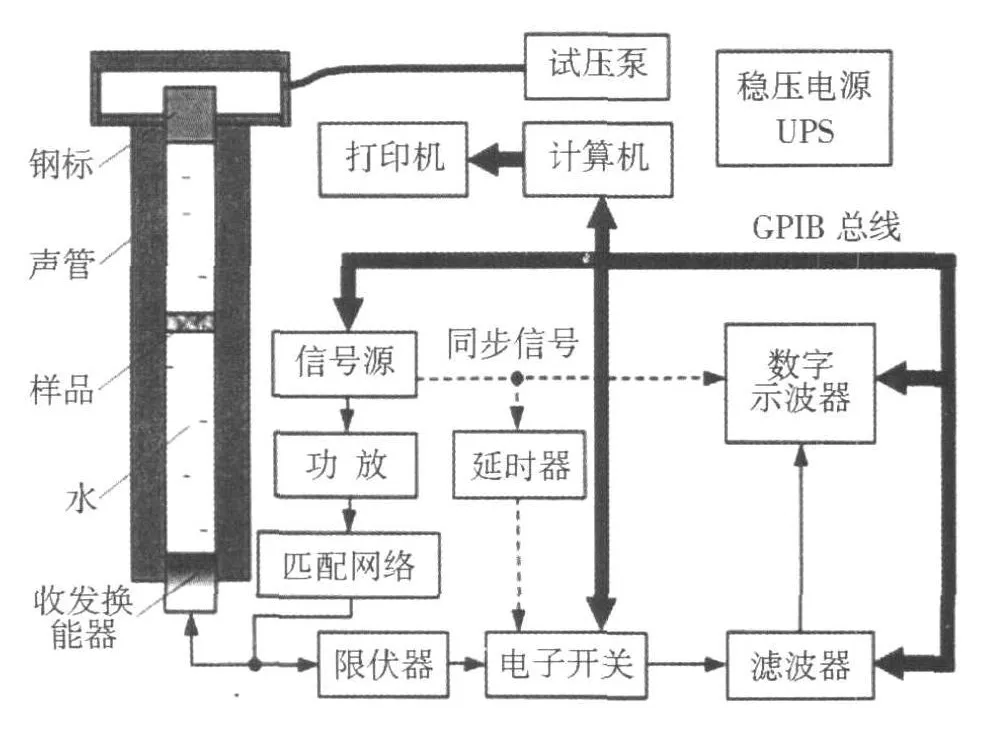
图3 声脉冲管法测试系统示意图

图4 尖劈样品实物

图5 不同静压下尖劈吸声系数计算曲线

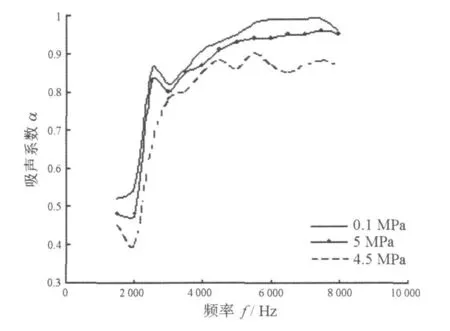
图6 不同静压下尖劈吸声系数实测曲线

对比图5和图6,吸声系数计算值和实测曲线吻合较好,另外还可以看出,4.5 MPa下尖劈材料的物理参数发生了较大突变,使得尖劈的吸声性能明显下降。因此,在设计吸声尖劈时,除要保证常压下尖劈具有良好的吸声性能外,还要保证尖劈材料的物理参数在高压下不发生突变。

3 空腔尖劈在声呐平台区中应用研究

由于声呐平台区为一复杂的混响场,其自噪声具有多声源特征,声呐平台区自噪声的预报除定量估算自噪声的量级大小外,还可以通过分析掌握不同噪声源对平台区自噪声的贡献量,为空腔尖劈的优化敷设方案提供依据,量化自噪声控制措施及其的技术指标[8]。

本文应用壳、梁和3D等单元构造一个接近于实艇的声呐平台一体化有限元模型,该模型不仅在形状上和实际结构相似,而且所有的几何参数和物理参数都是正确的。同时以腔尖劈材料力学参数及吸声性能测试数据作为数值试验的输入,采用集成分析软件VA ONE,以声呐平台结构模态密度为判据,低频采用FEM+BEM方法,中高频采用SEA方法,数值计算了10 Hz～3 kHz的振动激励下,敷设空腔尖劈的声呐平台区的结构振动及自噪声响应,从而验证空腔尖劈的吸声作用。

敷设空腔尖劈的声呐平台区自噪声预报的关键技术有:

(1)声呐平台区结构“一体化”技术。为平台区结构提供符合实际的有效支持,排除平台区因假设边界支承条件带来的误差;

(2)流固耦合处理。基于势流理论,采用BEM方法[9],开发了附连水质量三维计算程序,计算声呐平台区结构各阶湿模态的附加质量;

(3)空腔尖劈的处理。计算振动响应主要考虑材料的物理性能和几何参数,在求解辐射声压时考虑其吸声性能,数值分析空腔尖劈对声呐平台区声学特性的影响。

图7 声呐平台结构模型

图8 空腔尖劈几何模型

为了对比分析空腔尖劈的减振降噪作用,以及不同敷设方式对平台区振动和声辐射特性的影响,从吸声尖劈的敷设方式方面设计了三种计算工况。具体工况描述如表1所示:

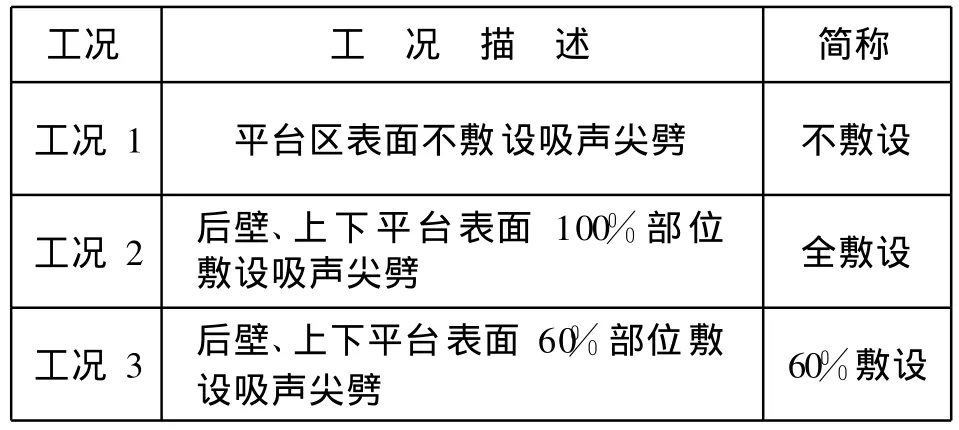
表1 空腔尖劈敷设工况

图9给出了声呐平台区自噪声总声压级不同敷设工况下的对比曲线。可以看出,空腔尖劈明显削弱了声呐平台区自噪声总声压级的峰值,曲线变化趋势和缓且全敷设与60%敷设工况曲线的变化趋势基本一致,其自噪声总声压级平均降低14 dB。60%敷设工况亦有较好降噪效果,声呐平台区自噪声总声压级平均降低11 dB,但是与全敷设工况相比中低频降噪效果要差一些。

图10给出了平台区后壁的辐射声压级不同敷设工况下的对比曲线。可以看出,后壁对声呐平台区自噪声总声级的贡献量最大,后壁的辐射声压级的幅值和变化趋势基本决定了平台区的自噪声特性。

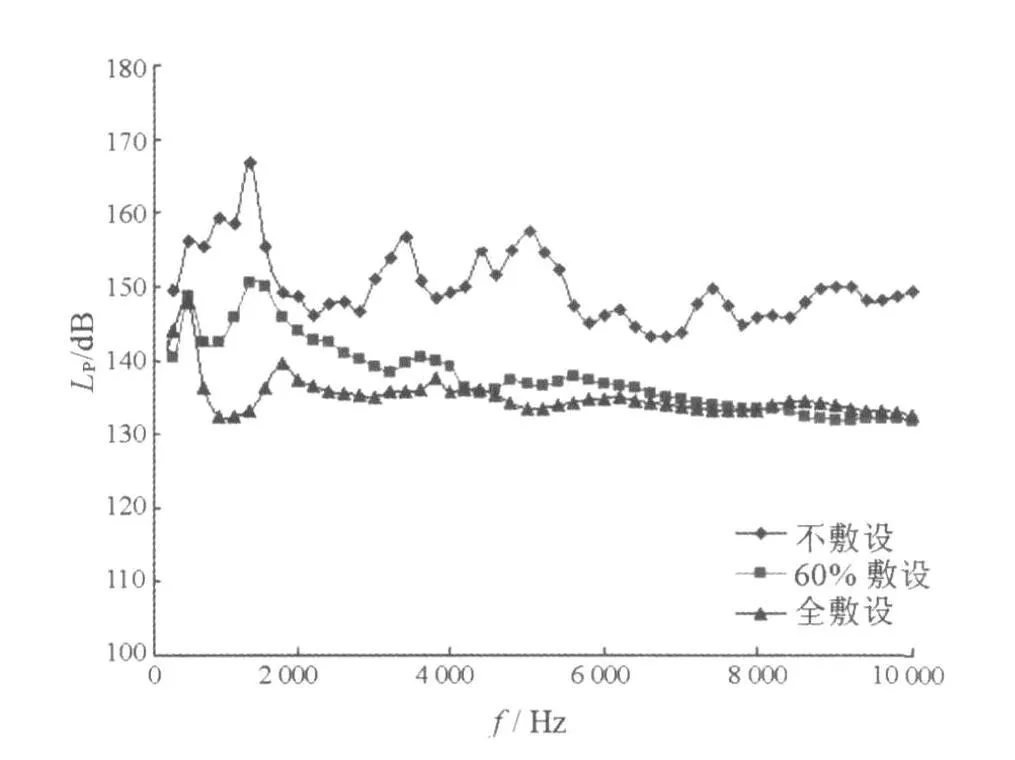
图9 自噪声总声压级对比曲线

图10 声呐平台区后壁自噪声对比曲线

从图11～图12可以看出(限于篇幅只给出部分结果曲线),空腔尖劈60%敷设工况下,上平台、声呐基阵安装位置的减振降噪效果甚至优于全敷设工况。因此,空腔尖劈的部分敷设方案既要考虑全频段声呐平台区的自噪声总声级,又要兼顾声呐基阵位置处的声压分布,从而最大程度地降低声呐平台区的自噪声,提高本艇声呐的探测距离和精度。

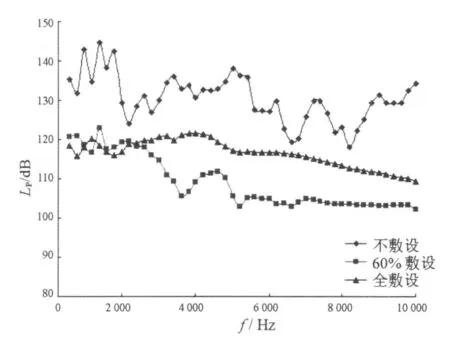
图11 声呐平台区上平台自噪声对比曲线

图12 声呐基阵处自噪声对比曲线

4 结 语

本文讨论了不同静压下尖劈吸声性能,开展了空腔尖劈声管测试,在此基础上,通过数值试验预报了声呐平台区的自噪声分布,对比分析了空腔尖劈敷设方案对其声学特性的影响,主要得到以下结论:

1)随着静水压力的增大,尖劈空腔形状和容积发生变化,吸声系数曲线形状基本不变。但第一谐振峰向高频移动,高静压下尖劈吸声系数下降较快;

2)空腔尖劈全敷设工况声呐平台区的减振降噪效果最好,平台区后壁对自噪声总声级的贡献量最大;

3)空腔尖劈的部分敷设方案既要考虑全频段声呐平台区的自噪声总声级,又要兼顾声呐基阵位置处的声压分布。

[1] GREMER L,HECKLM.Structure-borne sound[M].Berlin:Herdeiberg.N.Y.,1973.

[2] 王祖华,骆东平,肖邵予.潜艇首部声呐平台区中、高

频自噪声预报[J].舰船科学技术,1995,2:53～57.[3] 俞孟萨,叶剑平,吴有生等.船舶声呐部位自噪声的预

报方法及其控制技术[J].船舶力学,2005,(5):66～70.

[4] N.B.Miller.Reflections from gradual transition sound absorbers[J].Journal of the Acoustical Society of America,1958,30(10).

[5] 王仁乾,马黎黎,缪旭弘.带空腔尖劈吸声器吸声性能的研究[J].声学技术,1999,18(4):146～157.

[6] GIDEON M.Response of ribbed panels to reverberant acoustic fields[J].Journal of the Acoustical Society of America,1962,34(6):809～826.

[7] KoSH.Reduction of structure-borne noise using an airvoided elastomer[J].Journal of the Acoustical Society of America,1997,101(6):3306～3312.

[8] DhanakMR.Response of a sonar array to turbulent boundary layer noise on a cylinder[J].Journal of Sound and Vibration,1993,168(2):229～241.

[9] Von Estorff O.Boundary Element in Acoustics[M].WIT Press,2000.

[10] 缪旭弘,顾磊等.基于分层媒质模型的声学性能仿真研究[J].计算机仿真,2003,20(10):74～80.

[11] 姜闻文,陈光冶等.静水压变化下橡胶结构吸声性能的计算与分析[J].噪声与振动控制,2006,(5):55～57.

Acoustic Characteristics of Sonar Platform Laying of Cavity Wedge

Yao Xiongliang Ji Fang

sonar platform;cavity wedge;laying scheme;self-noise

This paper constitutes the sound absorption coefficient equations based on the non-uniform wave guide theory,discusses the wedge sound absorption ability with different hydrostatic pressures,and the results are compared with the sound pipe test of cavity wedge.Furthermore,the self-noise distribution of sonar p lat form is predicted through numerical experimentation and the influence of cavity wedge laying schemes to sonar platform acoustic characteristics is analyzed.The results show that the first resonance peak moves to the higher frequency with the increment of hydrostatic pressure,and the absorption coefficient of the cavity wedge decreases more sharply with the high hydrostatic pressure.The laying of cavity wedge obviously reduces the total self-noise level of the sonar platform,and the part laying method of wedge must consider the total self-noise level of platform in the full range of frequency bands,and also the sound pressure distribution of sonar array.

U661.44

A

1001-9855(2010)03-0029-06

2009-12-12

国防重点预研项目(40*********01);国际科技合作基金资助项目(2007DFR 80340)

姚熊亮(1963-),男,教授,博士生导师,主要从事船舶及海洋工程动力学研究。

计 方(1984-),男,博士研究生,主要从事船舶振动噪声控制。