船体纵骨的热点应力分析*

贵志飞 吴剑国 詹志鹄

(1.浙江工业大学建筑工程学院 杭州310014;2.中国船级社上海审图中心 上海 200135)

船体纵骨的热点应力分析*

贵志飞1吴剑国1詹志鹄2

(1.浙江工业大学建筑工程学院 杭州310014;2.中国船级社上海审图中心 上海 200135)

热点应力;应力集中系数;有限元分析;纵骨

运用MSC.Patran/Nastran软件,对典型船舶纵向构件进行了热点应力分析,讨论了4种不同因素对节点热点处的应力集中系数的影响,并总结了其变化规律。

0 引 言

疲劳破坏是船舶结构的主要破坏形式之一,各个节点连接处是疲劳强度的重要校核点。目前,对船体结构进行疲劳分析时,名义应力法是最简单也是应用最为广泛的方法。但是,在研究形状复杂的焊接接头疲劳强度时,难以明确地给出其名义应力,分析得到的结果分散性很大,且很难给出精确的SN曲线图。而采用热点应力评定时,可以对几类焊接节点形式给出一条S-N曲线,即以一条S-N曲线可以表示不同节点形式焊趾处的疲劳强度,因而可以大大减少节点形式按疲劳强度划分的级别[1],简化了节点形式,比用名义应力法具有一定的优越性。

热点应力方法最早应用于焊接管节点的疲劳分析,现在它的应用范围越来越广,已经发展到了所有类型的板结构。热点应力法的关键问题之一是确定热点应力值和应力集中系数。所谓的热点应力是指焊接构件节点处最为可能发生疲劳裂纹的起始点(通常在焊趾附近)的应力,多采用有限元计算或应变片实际测量法求解结构热点应力。目前,已有许多学者对此做了研究,如文献[2]、[3],规范[4]中也已给出了一个应力集中系数综合表,但并不够详细。

本文是在此基础上,运用MSC.Patran/Nastran软件,对典型的船舶纵骨进行了热点应力分析,讨论了4种不同因素对节点热点处的应力集中系数的影响,并总结了其变化规律,对规范中应力集中系数综合表做进一步的补充。

1 热点应力法的基本原理

1.1 热点应力计算

一般情况下用单元表面最大主应力值计算热点应力δh

[5],因为与裂纹扩展方向垂直的±45°范围内的最大正应力对疲劳裂纹的扩展起关键作用。所以本文运用两点线性外推法,取单元表面插值点处的最大主应力值进行线性外推,计算得到热点应力值,如下式所示:

式中 σt/2、σ3t/2——距焊趾t/2、3t/2处的最大主应力值,其中t为板厚;

若网格划分时无法控制在t/2及3t/2点处,这两点处的应力σ应根据所选有限元节点处的应力用Lagrange插值法求得,如图1所示。计算公式为:

式中:σ1、σ2、σ3、σ4——有限元节点1、2、3、4处的最大主应力值;C1C2C3和C4为系数,应按下列各式计算:

式中 x──插值点距焊趾的距离,mm;

x1、x2、x3、x4──有限元节点1、2、3、4距焊趾的距离,mm。

图1 热点应力计算方法

1.2 应力集中系数

热点应力与名义应力的比值称为应力集中系数,且应按下式计算:

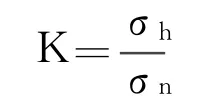
式中 σh——热点应力,N/mm2;

σn——名义应力,N/mm2。

本文名义应力值的计算是根据纵骨上的弯曲应力范围计算公式计算:

式中 S3e——海水动压力作用下纵骨的弯曲应力范围,N/mm2。

s──纵骨间距,cm;

l──纵骨跨距,跨距点取在沿端部肘板高度方向上,从纵骨面板量起至等于纵骨一半腹板高度的点,cm;

Ws──纵骨连带板的净剖面模数,cm3;

x──纵骨端部到疲劳计算点的距离,cm。

参见文献[4];

Δp──作用在纵骨上的海水动压力范围,kN/mm2。

2 纵骨热点应力计算模型

本文有限元模型采用四节点板壳单元,热点附近的单元尺寸不大于受力构件的厚度,范围按下面的规定选取:

(1)纵向范围从热点处向前后分别延伸2个纵骨跨度,两端的强框架并未建模;

(2)横向范围从热点处向左右分别延伸2个纵骨间距;

(3)垂向范围延伸至内底板处。

由于只考虑节点在侧向压力作用下热点处的应力集中系数的变化规律,所以只在模型的底板处施加侧向压力。由于内底结构(包括垂向挺筋端部)离热点分析区域有足够的距离,根据圣维南原理,内底结构的边界条件对热点处应力影响不大,改变其端部边界条件试算表明了这一点,故取内底处的边界条件为固定。模型纵向两端、横向两侧由于对称性,也均取固定。具体有限元模型见图2。

图2 有限元模型

本文是以一艘27 000 t散货船中的纵骨节点为热点应力评估对象,通过比较分析,随着侧向压力值的变化,热点处的热点应力值和名义应力值都将发生变化,而由两者相比所得的应力集中系数几乎保持不变,且当改变底板厚度时,也能得到上述一致结论,具体分析过程可参见本文作者的后续论文。

3 不同节点形式的计算及结果

本文主要考虑了纵骨节点的加水密补板和非水密补板两种节点连接形式,如图3所示。

图3 精细网格的有限元模型

为了改善纵骨端部的局部应力范围,可通过加大纵骨尺寸、改善纵骨形式、以及添加肘板等方式[6],本文考虑了四种相关因素对两种节点形式疲劳性能的影响。具体如下:

(1)软踵尺寸改变对结构的影响;

(2)软趾尺寸改变对结构的影响;

(3)软趾圆弧半径改变对结构的影响;

(4)加设背肘板对结构的影响。

对有限元分析得到的节点应力值进行了分析和整理,得到一系列热点应力值对应的应力集中系数,如图4～图11,并将所得的热点应力集中系数汇总于表1。

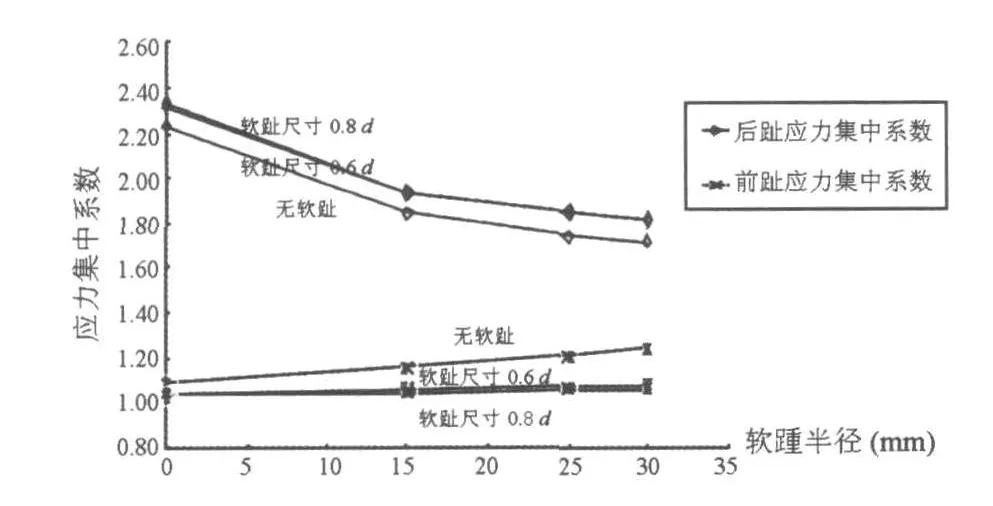
图4 软踵半径变化(非水密)

图5 软踵半径变化(水密)

图6 软趾尺寸变化(非水密)

图7 软趾尺寸变化(水密)

图8 软趾半径变化(非水密)

图9 软趾半径变化(水密)

图10 背肘板半径变化(非水密)

图11 背肘板半径变化(水密)

表1 侧向压力下应力集中系数汇总表(不考虑横舱壁与横向框架之间相对位移)

注:a为纵骨节点后趾,f为纵骨节点前趾。

由此可见:

(1)开设软踵时,节点后趾的热点应力值和应力集中系数减小,而前趾热点应力值和应力集中系数几乎保持不变。逐渐加大软踵的半径值,前趾和后趾的热点应力值及应力集中系数几乎保持不变。所以对节点踵部进行开孔处理,能够有效改善节点的疲劳性能,但过大的开孔并不能进一步改善其疲劳性能;

(2)在同一软踵下,设置软趾能有效减小前趾的热点应力值和应力集中系数,但会增大后趾的热点应力值和应力集中系数;

(3)随着软趾尺寸的增大,后趾的热点应力值及应力集中系数略有增大,前趾的热点应力值略有减小,而前趾的应力集中系数几乎保持不变。对不同的软踵开孔半径值,前后趾的热点应力值和应力集中系数变化的趋势相同;

(4)设置背肘板能够较为显著的减小后趾的热点应力值和应力集中系数,可见这是改善节点疲劳性能较为有效的途径;

(5)通过对节点加水密补板和非水密补板的两种连接形式的有限元分析可知,两者规律基本相同。未加设背肘板时,在前趾处,节点两种连接形式的热点应力值和应力集中系数相差不大;在后趾处,加非水密补板连接形式算得的应力集中系数较大。在加设背肘板时,节点两种连接形式的前后趾热点应力值和应力集中系数都相差不大。

4 结 语

本文以一艘27 000 t散货船中的纵骨节点为研究对象,总结了部分因素对其热点处应力集中系数的影响规律。但纵骨的腹板高度与纵骨跨距之比不同,以及内外底纵骨间垂向挺筋的腹板高度和长度与纵骨跨距之比不同都会对其应力集中系数有所影响,此还有待继续研究。

[1] 霍立兴.焊接结构的断裂行为及评定[M].北京:机械工业出版社,2000.

[2] SHI Li-juan,CUI Wei-cheng.An Investigation into the Uncertainty in the Calculated Hot-spot Stresses of a Shipside Structure Detail[J].Journal of Ship Mechanics,2002,6(6):85～91.

[3] WAN Zheng-quan,XU Bing-han.Stress Concentration Factors of Cutout for Longitudinal[J].Journal of Ship Mechanics,2002,6(3):28～36.

[4] 钢质海船入级规范(2006)[M].中国船级社,2006.4.

[5] Hobbacher A.Recommendations for fatigue design of welded joints and components[C].IIW Document XIII-1539-96/XV-845-96,Update June 2002.23～31.

[6] 邱海荣.基于双壳油船结构共同规范的疲劳损伤计算[D].大连理工大学硕士研究生学位论文,2006.12.

Hot Spot Stress Analysis of Hull Longitudinals

Gui Zhifei Wu Jianguo Zhan Zhihu

hot spot stress;stress concentration factor;finite element analysis;long it udinals

Based on the method of hotspotstress,a typical form of hull long it udinals is analyzed in this paper by MSC.Patran/Nastran software.This paper discusses the influences of four different factors on stress concentration factor(SCF)for hot spots of ship connections,and summarizes their variation trend line.

U663.2

A

1001-9855(2010)03-0011-05

2009-11-30

贵志飞(1985-),男,汉族,浙江衢州人,硕士研究生,主要从事钢结构分析与研究工作。

吴剑国(1963-),男,汉族,江苏吴县人,教授,主要从事钢结构分析与研究工作。

詹志鹄(1970-),男,汉族,湖北人,高级工程师,主要从事船体结构强度分析和研究工作。