直扩系统中IIR格型滤波器抑制窄带干扰新方法与性能分析

龚文飞 吴嗣亮 李加琪

①(北京理工大学信息与电子学院 北京 100081)②(北京交通大学电子信息工程学院 北京 100044)

1 引言

直接序列扩频(DSSS)通信技术以其良好的隐蔽性、保密性、抗多径衰落特性以及抗干扰能力而被广泛应用于军事通信、卫星通信、移动通信等领域。但是，当干扰强度超出扩频增益所能够提供的抑制能力时，需要采取一定的信号处理手段来增强系统抗强干扰能力[1−2]。

在现有的众多抑制窄带干扰的信号处理手段中，时域自适应陷波干扰抑制技术具有实现简单、抗干扰性能好等优点而受到人们的广泛重视[3−5]。二阶IIR陷波器按照结构可以分为直接型和格型两种，相比直接型IIR陷波器，因格型IIR陷波器不仅可以准确地控制滤波器的陷波频率，也可以准确地调整陷波器的带宽，同时具有更好的收敛特性以及更为准确的频率估计[6]，且对有限字长效应敏感性比较低，成为近来研究较多的窄带干扰抑制方法。格型IIR陷波器的性能与陷波频率估计精度和陷波深度有关，Regalia提出一种非梯度搜索的格型自适应算法[7]，简化了运算量，然而该方法在收敛后，陷波频率存在偏移，影响了陷波性能。文献[8]采用全局输出信号作为参数调整的反馈信号，降低陷波频率偏移的影响。文献[9]通过调整陷波器的陷波深度来提高系统的抗干扰性能。上述方法分别从运算量、陷波频率和陷波深度的角度研究了陷波器的性能，对最优陷波带宽的选择上却未曾提及。为了提高陷波性能，统筹考虑陷波频率、陷波带宽和滤波器的收敛速度和实时性，本文提出了一种时域和频域相结合的窄带干扰抑制方法，先对接收信号进行最优加窗处理和FFT变换。由于窄带干扰将在频域出现极大的峰值，采用了频谱校正技术，实现干扰频率的精确估计，同时根据干扰频率的估计精度和干信比(JSR)来控制陷波的宽度和深度，自适应地调整IIR格型陷波器中的对应的陷波频率参数，更有效地实现窄带干扰的抑制。

2 自适应IIR格型陷波器

二阶自适应IIR格型陷波器的传递函数H(z)为

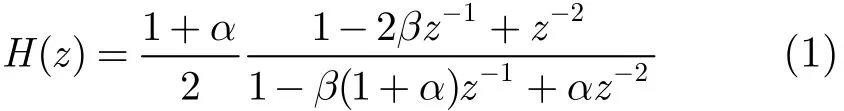
其对应的结构如图1所示。

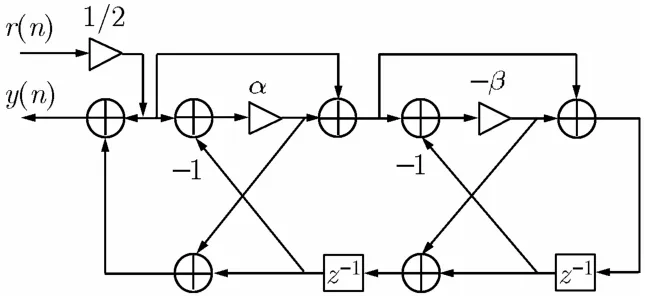
图1 二阶格型IIR陷波器

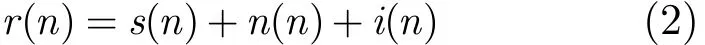
设经过A/D采样后直接序列扩频信号由3部分组成，即式中r(n)是接收到的含有窄带干扰的和加性高斯白噪声的卫星导航信号，s(n)是卫星导航信号，n(n)是高斯加性白噪声，i(n)是窄带干扰。这里取单频正弦信号作为窄带干扰模型，其表达式如下：

接收到的卫星导航信号经过IIR陷波器之后，输出信号的功率可以表示为

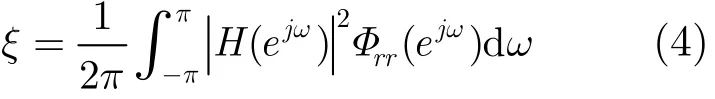
式中|H(ejω)|2是系统响应函数的模平方，(ejω)是接收到的含有窄带干扰的和加性高斯白噪声的卫星导航信号的功率谱，它们分别可以表示为[10]

式中Φss(ejω)为卫星信号的功率谱密度，是加性高斯白噪声的方差。

由于卫星信号的功率和加性高斯白噪声的功率相比干扰的功率小很多，这里假定(ejω)=0，=0。则输出信号的功率可以表示为

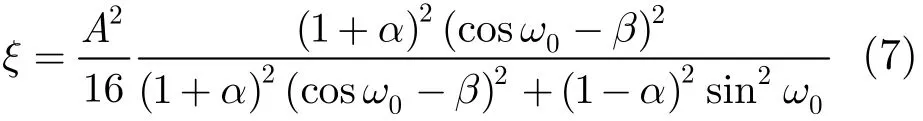
因为所采用的是IIR窄带陷波器，在输入信号功率一定的情况下，通过改变不同的陷波位置，也即改变参数β，输出信号的功率ξ应该存在最小值。由式(7)可知，β=cos ω0可使输出功率最小。

考虑到实际工作中，干扰信号的频率难以做到很精确的估计，所以选择陷波带宽要包含频率估计的误差区间。，设频率估计的误差区间为ω1＜ω＜ω2，对应的干信比为JSR，为了达到干扰的完全抑制，当ω1＜ω＜ω2，应有如下不等式成立

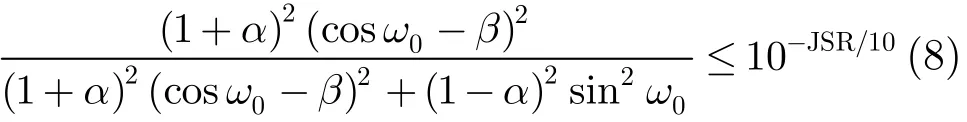
为了在干扰完全抑制的情况下做到有用信号损失最小，可令陷波带宽Δω=ω2−ω1，则当ω=ω1和ω=ω2时，式(8)的等号成立，从而可以求得

由式(9)可以看出，陷波带宽系数α是陷波带宽Δω单调函数，在一定信干比JSR条件下，随着α逐渐接近于1，陷波器的带宽逐渐减小；干扰检测模块检测到没有干扰存在时，可以将设置α=1，此时滤波器变成一个直通滤波器，对有用信号没有损失。

3 基于IIR格型滤波器抑制窄带干扰新方法

图2所示的是本文提出的时域与频域相结合的窄带干扰抑制原理框图。接收到的卫星导航信号经A/D转换后分为两路，分别送入频域处理模块和时域处理模块。其中，频域处理模块由最优加窗模块、FFT变换模块、干扰检测模块、频谱校正模块和IIR陷波系数生成模块组成。时域处理部分由IIR格型陷波模块构成。

为了充分提高系统的实时性，在陷波处理过程中，时域处理部分仅仅做IIR陷波，而较为复杂IIR陷波参数估计过程由频域处理来完成。尽管当前用于时域滤波的IIR陷波器系数是由前一时间单位接收到的数据块估计出来的，但在实际电磁环境中，干扰信号比较稳定，所以该方法对干扰抑制效果几乎不会产生影响。与传统的基于FFT频域干扰抑制方法相比，不仅其复杂度大大降低，而且实时性却有很大提高。

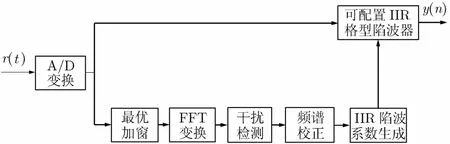
图2 改进的时域频域相结合窄带干扰抑制框图

在有用信号损失最小化的情况下要实现干扰得到最大化抑制，干扰频率的精确估计和最优陷波带宽的选择是关键。

3.1 干扰频率精确估计

要实现窄带干扰的有效抑制，干扰信号频率的精确估计是关键。由于FFT变换谱峰搜索存在栅栏效应，为了精确估计干扰信号的频率，可考虑通过时域加窗的方法来降低栅栏效应的影响[11,12]，同时选择易于工程实现的幅度比值频谱校正方法来进行频谱校正。较窄的窗函数主瓣和较低的旁瓣有利于提高频率校正精度。但是主瓣窄和旁瓣小本身是一对矛盾，因此，在实际应用中，要根据需要，综合考虑折中的办法选取最优窗函数。

在FFT频谱检测中，广义余弦类窗函数较为常用，其表达式为

式中的K和ai确定了不同类型的窗函数。

综合硬件所能支持的计算量和窗函数性能考虑，选择K=2情况下的最优窗函数，具体参数选择为a0=3/8，a1=1/2，a2=1/8[13]。

由Rife频率估计方法[14]可以推导出K=2情况下的最优窗函数下的估计值为

因Rife频率估计方法由最大值和次大值两个点进行线性插值来实现的，所以也可以考虑采用由最大值连同临近最大值的左右的各一个点采用抛物线插值和牛顿插值来实现频率估计。通过下面的仿真比较了3种插值方法的频率估计性能。

仿真条件：输入信号为含有窄带干扰的和加性高斯白噪声的卫星导航信号，卫星信号为调制PN码的GPS卫星信号，干扰信号为单频正弦信号，干信比为60 dB，信噪比为-37 dB。信号采样频率为64 MHz，FFT点数取N=1024，选择窗函数为K=2情况下的最优窗函数进行加窗处理，信号频率与其FFT幅度最大处对应频率的相对偏差δ以0.01为单位步进，变化范围为0～0.5，对每一个频率偏差分别做100次Monte-Carlo实验。最后得出频率估计 (以Δf=1/T 为单位)的均方根误差随相对偏差δ的变化关系如图3所示。

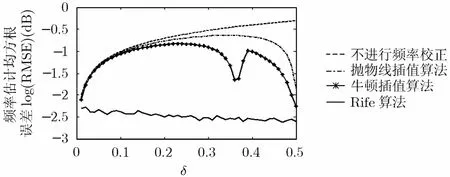
图3 不同的频谱校正方法性能比较

通过仿真可以看出用线性插值的Rife方法优于用抛物线插值法和牛顿插值法，原因在于对于单频干扰信号，在干信比较大的情况下，随着逐渐增大，幅度第3大的谱线所对应的幅度相比最大值和次大值来说迅速减小，最小可以小2～3个数量级，这会给插值带来很大的误差。但此时采用Rife频率估计方法效果更好，另外Rife方法也更易于硬件实现。

3.2 最优陷波带宽分析

在干扰被有效抑制的情况下，根据频率估计的误差来选择合适的陷波宽度是减小有用信号损失的关键。为了分析Rife方法的频率估计误差与干噪比及FFT长度的关系，设U0=real(Z0)，U1=real(Z1)，其中Z0和Z1分别为叠加在频谱最大值A0与次大值A1上的噪声，其表达式分别为

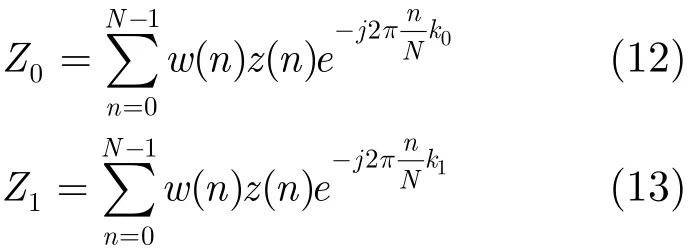
式中w(n)为最优窗函数，z(n)=s(n)+n(n)为输入扩频信号加信道噪声，直扩系统中扩频信号s(n)可以近似看成一个白噪声，信道噪声n(n)是服从高斯分布的白噪声，在扩频增益比较大时，到达接收机的信号功率可以远小于接收机的噪声功率(例如在典型的扩频系统GPS卫星导航系统中，卫星信号到达地面用户接收机时相当微弱大约为-160 dBW，比接收机热噪声还要低约30 dB)，因此在频域上扩频信号s(n)的频谱的幅度远小于信道噪声n(n)的频谱的幅度。由DFT变换的过程可知，Z0和Z1可以看成是输入序列z(n)分别经过中心频率为2π(k0/N)和2π(k1/N)、频率响应为的窄带滤波器之后采样的输出，所以Z0和Z1可以近似看作是窄带高斯噪声。

在干噪比JNR比较大的情况下，接收到的含有窄带干扰的和加性高斯白噪声的卫星导航信号r(n)=s(n)+n(n)+i(n)的DFT在最大和次大谱线处的幅度可以分别近似表示为[15]

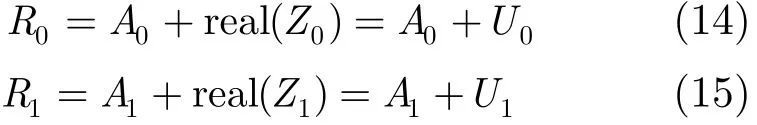
由式(11)可知

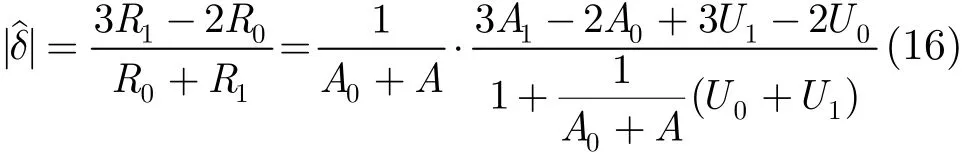
将式(16)进行泰勒级数展开，在干噪比JNR比较大的情况下，忽略高次项，于是的估计值可以近似表示为

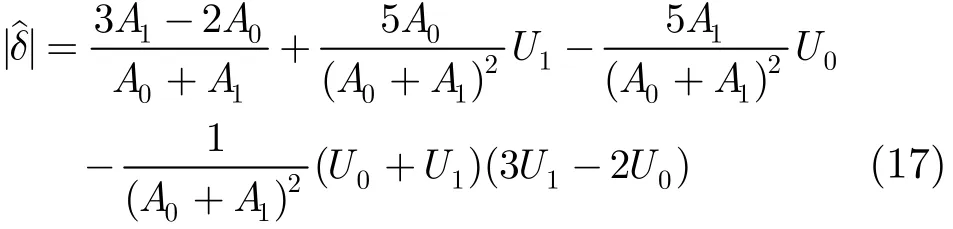
在干噪比JNR比较大、频率分辨率比较高的情况下，式(17)的最后一项远小于前三项，可以忽略不计，所以式(17)又可以近似表示为

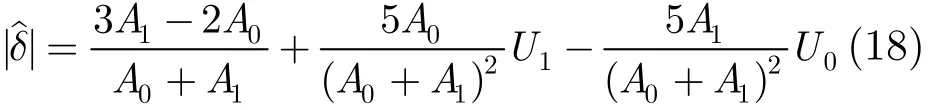
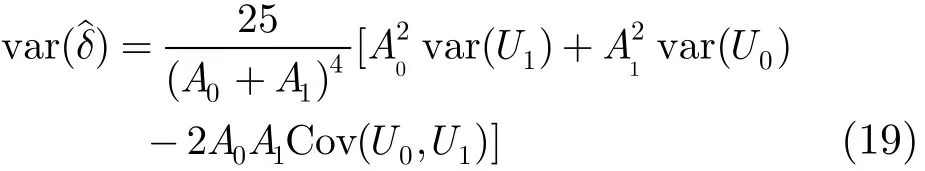
由式(14)和式(15)可知

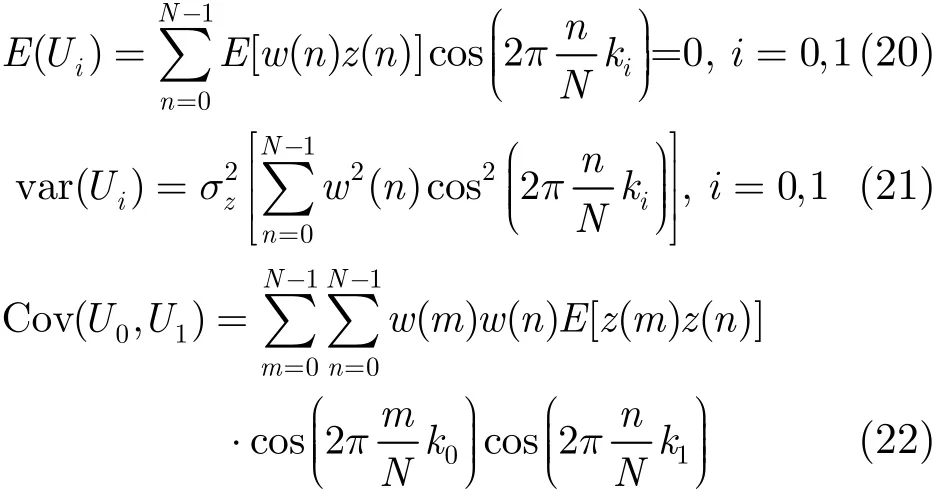
由于z(n)可以看成是白噪声序列，当m≠n时，E[ z(m) z(n)]=0，所以式(22)可以简化为

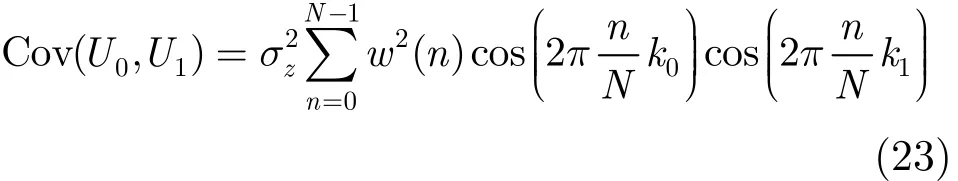
为了验证理论分析结果与仿真结果的相符合，进而求出最优陷波带宽，这里假定式(18)中的估计为的无偏估计，则估计值|δ|的均方根误差为

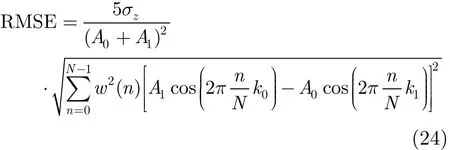
图4是在同2.1节中的仿真条件下的理论推导的估计值|δ|的均方根误差与Monte-Carlo仿真的频率估计均方根误差的比较曲线，由图可以看出，理论推导结果和仿真结果基本相符，随着的增大，估计误差逐渐降低，这是由于随着的增大，次大谱线的幅度相比噪声的幅度越来越大，也即噪声对次大谱线的影响越来越小，从而估计估计精度越来越高。

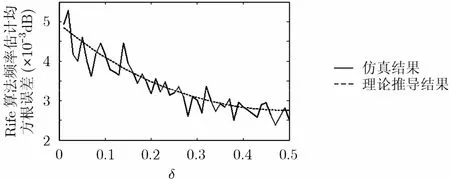
图4 Rife方法的频率估计误差理论推导与仿真结果

设最优陷波带宽为Δω，为了使干扰得到尽量抑制，陷波带宽Δω应该包含的估计误差区间，为了定量表示≤+Δω/2的概率，这里取

由于U0和U1可以近似认为高斯分布，设x=A0U1, y=A1U0，则x和y联合概率密度函数可以表示为

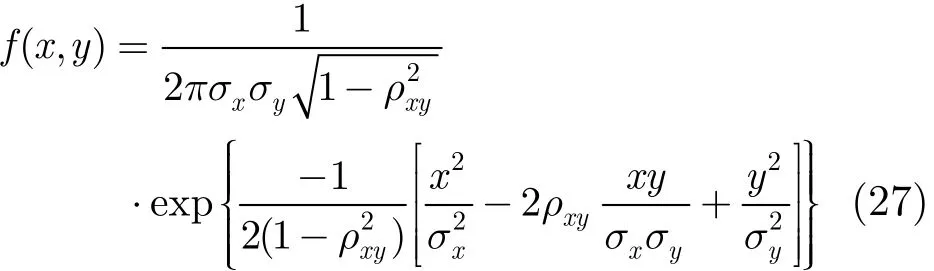
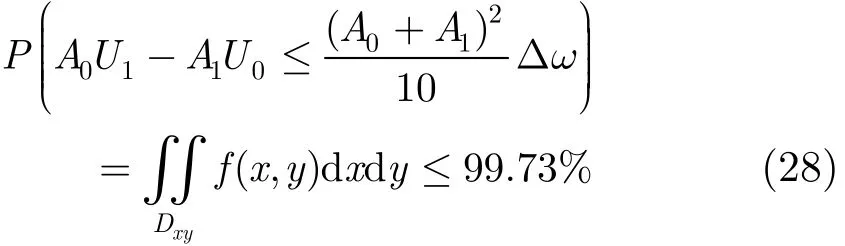
式中Dxy对应与区间：

4 性能仿真

为了验证本文所提出基于频谱校正的时域频域相结合的窄带干扰抑制方法的性能，这里对其进行了如下仿真。

仿真条件设置如下：输入信号为含有窄带干扰的和加性高斯白噪声的卫星导航信号，为了便于比较，干扰信号为单频正弦信号，干信比为60 dB，信噪比为-37 dB，扩频码取GPS的PN码，扩频码速率为10.23 MHz。选择窗函数为K=2情况下的最优窗函数进行加窗处理，为了方便与FFT 本身的频率分辨率Δf=1/T 对比, 下面在仿真过程中均采用干扰信号频率与其DFT幅度最大处对应频率的相对偏差δ来进行分析。信号采样频率为64 MHz，有用信号的中心频率为15.5 MHz，干扰信号的频率为15.5 MHz+δΔf，相对偏差δ以0.01为单位步进，变化范围为0-0.5，对每一个频率偏差分别进行有无频谱校正的窄带陷波，从而对比两种情况下，陷波器性能随相对偏差δ的变化曲线。FFT变换的点数取N=1024。

图5比较了5系数开环FIR滤波[16]，开环IIR陷波[9]和本文陷波方法陷波之后的信干噪比SJNR与信干比SJR随相对频率偏差δ变化曲线。图 5(a)为信干比SJR随相对频率偏差δ变化曲线，由图可见，不同的频率偏差下，没有采取频谱校正的窄带陷波之后信号的干信比差别很大，尽管开环FIR方法陷波输出的SJR高于本文方法，但这是以牺牲有用信号为代价的，且两者输出的SJR均大于零，也即滤波以后干扰远远低于噪声，对总的信干噪比几乎没有影响。由于本文输入信干噪比和频率估计误差选择最优的陷波带宽，在干扰被有效抑制的情况下减小了有用信号的损失，由图5(b)信干噪比SJNR随相对频率偏差δ变化曲线可以看出，本文方法陷波之后输出的信干噪比较开环IIR陷波方法信干噪比改善最大接近1.13 dB，较开环FIR方法信干噪比改善最大接近1.68 dB。

图6从误码率的角度仿真验证了本文不同频率偏差下不同陷波的方法的性能，对应误码率理论值表达式为信噪比为-37 dB对应的载噪比C/N0=36 dBHz ，数据率取500 bps，仿真数据比特数为1000000。由图可以看出，本文所采用的陷波方法的性能最好，更接近于理论值；开环IIR陷波方法性能随着相对频率偏差δ变大而逐渐变差；开环FIR方法性能最差，不同频率偏差下误码率趋于一定值，这主要是开环FIR方法陷波带宽较大，且大于最大频率偏差，但这带来了更多有用信号的损失，致使抗干扰性能下降。

图5 不同频率偏差下陷波的性能比较

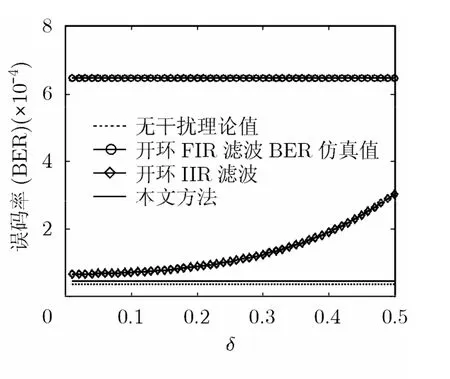
图6 不同频率偏差下陷波的误码率性能比较

5 结论

本文提出了基于IIR格型陷波器时域频域相结合的窄带干扰抑制新方法，运用符合稳定性和实时性要求的时域频域并行陷波处理结构，采用频谱校正技术精确地估计出干扰信号的频率，根据频率误差确定出最优陷波带宽，从而在有用信号损失达到最小情况下有效抑制干扰。较大程度地改善了接收机在窄带干扰环境下的工作性能，是一种工程实用性较高的抗窄带干扰方法。

[1] Milstein L B. Interference rejection techniques in spread spectrum communications [J]. Proceedings of the IEEE, 1988,76(6): 657-671.

[2] 徐向东，孟藏珍，袁俊泉. 基于递归最小二乘的DS-SS系统抗窄带干扰技术[J]. 电子与信息学报, 2007, 29(11):2779-2782.Xu Xiang-dong, Meng Cang-zhen, and Yuan Jun-quan. The technique of narrowband interference rejection for DS-SS systems based on RLS algorithm [J]. Journal of Electronic &Information Technology, 2007, 29(11): 2779-2782.

[3] 郭艺，王世练，张尔扬. 适应开环FIR滤波器抗窄带干扰方法研究[J]. 电子与信息学报, 2007, 29(4): 959-962.Guo Yi, Wang Shi-lian, and Zhang Er-yang. Study on open-loop adaptive FIR filter approach for interference suppression [J]. Journal of Electronic & Information Technology,2007, 29(4): 959-962.

[4] 张春海，朱江，王世练等. 可用于DSSS系统时变干扰抑制的IIR滤波器设计[J]. 信号处理, 2007, 23(4): 495-499.Zhang Chun-hai, Zhu Jiang, and Wang Shi-lian, et al.. The design of IIR filters for time-varying interference suppression in DSSS communication systems [J]. Signal Processing, 2007,23(4): 495-499.

[5] Qin P and Cai P. A novel algorithm of adaptive IIR lattice notch filter and performance analysis [J]. Journal of Shanghai University (English Edition), 2007, 11(5): 485-489.

[6] Cho N and Lee S. On the adaptive lattice notch filter for the detection of sinusoids [J]. IEEE Transactions on Circuits and Systems, 1993, 40(7): 405-416.

[7] Regalia P A. An improved lattice-based adaptive IIR notch filter [J]. IEEE Transactions on Signal Processing, 1991,39(9): 2124-2128.

[8] 张世平，赵永平，张绍卿等. 一种改进的自适应格型陷波算法及其收敛性分析[J]. 电子学报, 2004, 32(2): 338-341.Zhang Shi-ping, Zhao Yong-ping, and Zhang Shao-qing, et al..A modified adaptive algorithm of lattice notch filter and its convergence analysis [J]. Acta Electronica Sinica, 2004, 32(2):338-341.

[9] Won J and Cho N. Narrow-band interference suppression in direct sequence spread spectrum systems using a lattice IIR notch filter. In Proc. IEEE ICASSP'2001, Salt Lake City,2001, 4: 2236-2240.

[10] Hirano K, Nishimura S, and Mitra S. Design of Digital Notch Filters [J]. IEEE Transactions on Communications, 1974,22(7): 964-970.

[11] Dusan A. Dynamics of frequency estimation in the frequency domain [J]. IEEE Transactions on Instrumentation and Measurement, 2007, 56(6): 2111-2118.

[12] Irini S R, Branimir D R, and Veljko D P. Extremely flat-top windows for harmonic analysis[J]. IEEE Transactions on Signal Processing, 2007, 56(3): 1025-1041.

[13] 王晓君，陈禾，仲顺安. 改进的脉冲雷达信号加窗DFT频谱校正算法[J]. 北京理工大学学报, 2008, 28(2): 164-167.Wang Xiao-jun, Chen He, and Zhong Shun-an. Improved correction algorithm of windowed DFT spectrum for pulsed radar signal [J]. Transactions of Beijing Institute of Technology, 2008, 28(2): 164-167.

[14] 王旭东，刘渝，邓振淼. 基于修正Rife算法的正弦波频率估计及FPGA实现[J]. 系统工程与电子技术, 2008, 30(4):621-624.Wang Xu-dong, Liu Yu, and Deng Zhen-miao. Modified Rife algorithm for frequency estimation of sinusoid and implementation in FPGA [J]. Systems Engineering and Electronics,2008, 30(4): 621-624.

[15] 齐国清，贾欣乐. 插值FFT估计正弦信号频率的精度分析[J].电子学报, 2004, 32(4): 625-629.Qi Guo-qing and Jia Xin-le. Accuracy analysis of frequency of sinusoid based on interpolated FFT [J]. Acta Electronica Sinica, 2004, 32(4): 625-629.

[16] Amin G M. Interference Mitigation in Spread Spectrum Communication Systems Using Time-Frequency Distributions [J]. IEEE Transactions on Signal Processing, 1997,45(1): 90-101.