基于最大自相关及最小能量比的MB-OFDM-UWB系统定时算法

戈立军 赵迎新 吴 虹 金宇昂

(南开大学信息技术科学学院 天津 300071)

1 引言

超宽带(UWB)无线通信技术具有功率谱密度低、传输速率高、抗多径干扰能力强等特点，将被应用于短距离高速无线通信、穿透成像和测量等方面。实现UWB的体制有多种，其中多频带正交频分复用(MB-OFDM)技术被建议作为室内个人通信IEEE 802.15.3a的物理层标准[1]，并被欧洲ECMA-368标准采纳[2]。正交频分复用(OFDM)是一种高效的数据传输技术，它通过相互正交的子载波并行的传输数据，频带利用率高，抗多径干扰能力强。OFDM技术已在通信等领域得到广泛的应用，例如欧洲标准DAB，DVB，ADSL，IEEE802.11a和HIPERLANⅡ等。在传统窄带OFDM系统中，若定时偏差超前但不超过保护间隔，则只带来子载波间干扰(ICI)，需要用信道估计的方法在频域补偿，若滞后则还会带来符号间串扰(ISI)，造成信噪比损失，系统性能严重下降[3]。

文献[1,2]提出的MB-OFDM超宽带系统与传统单频带OFDM系统不同，具有以下特点：不同频带具有不同的信道响应和载波频偏；对于功率受限的UWB系统，采用零后缀(ZP)而不是循环前缀(CP)以避免功率损失；采用由时频码控制的跳频机制，从而错误的定时位置会造成错误的解跳频，系统性能极具恶化。目前已有一些关于MB-OFDM系统定时同步的文献，但是针对ECMA-368标准并同时给出帧检测及粗细定时完整方案的文献很少。文献[4]给出了UWB信道下定时偏差对OFDM系统的影响。文献[5,6]采用基于信道估计序列的最大似然估计(ML)法，利用信道信息进行细定时。文献[7]采用最大后验概率(MAP)法，性能好于ML法，但是需要已知信道分布参数。ML法和MAP法都基于传统CP-OFDM系统，且需要先信道估计，故较为复杂。文献[8]给出了无需信道估计的基于ZPOFDM系统的盲符号定时同步方法，但是没有阐述如何将其应用于多频带系统及能量比值的比较范围。在文献[9]中，粗细定时同步均采用基于同步序列的最大自相关法，但此法为多径受限，其细定时位置表示的仍是最强径，而不一定是第1径，所以细定时后误差仍较大。另外，对于UWB的ZPOFDM系统，较小的定时偏差可以通过重叠相加(OLA)法进行频域信道均衡的同时来补偿[10]。设保护间隔长度为Ng，多径数为L，则OLA法可描述为将定时后的OFDM符号的最后Ng个数与开头Ng个数相加并置于开头，使ZP-OFDM符号变成等效的CP-OFDM符号。当残余定时偏差d属于[-(Ng-L),0]时，重叠相加操作后相当于OFDM符号在时域的循环移位，故可以在频域用导频来补偿，否则将引入ISI，使系统性能下降。本文在综合已有研究基础上，通过进一步算法改进和仿真给出了适用于标准多频带OFDM超宽带系统的定时同步的完整方案，旨在通过适当的定时算法把残余定时偏差控制在[-(Ng-L), 0]范围内，从而可以利用OLA法连同信道一起来补偿。用基于前导序列第1频带信息的最大自相关法进行帧检测及粗定时，用基于全部3个频带信息的最小能量窗比值法进行细定时，研究表明该定时同步方案具有良好的性能以及较低的复杂度。

2 系统参数及信道模型

ECMA-368标准规定了一种超宽带的MBOFDM系统，系统简要框图如图1所示。该系统传输速率可高达480 Mbps，频带使用未划分的3.1 GHz-10.6 GHz，并将其分为14个子频带，每个子带带宽为528 MHz，3个子带为一组，时频码控制的跳频机制实现射频部分载波中心频率的转换。FFT长度为128，其中包括100个信息子载波、12个导频子载波、10个保护子载波、1个直流子载波和5个空子载波。发送端IFFT后加入长度为37的ZP作为保护间隔，组成长度为165的OFDM符号。每帧开始为前导序列，由24个同步符号及6个信道估计符号组成。同步序列在时频域的结构如图2所示，其时频码为1，2，3，1，2，3。

图1 MB-OFDM-UWB系统简略框图

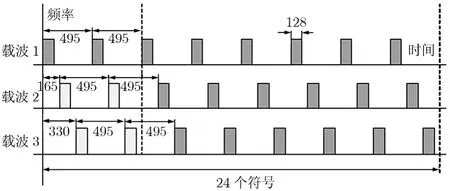
图2 前导同步序列

IEEE 802.15.3a工作组推荐的UWB信道冲激响应可以表示为[10]

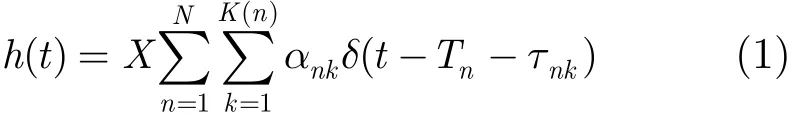
其中X是对数正态随机变量，代表信道的幅度增益；N是观测到的簇的数目，K(n)是第n簇内收到的多径数目，α=pnkβnk，pnk为等概率+1和-1的离散随机变量，βnk是第n簇中第k条路径的服从对数正态分布的信道系数。Tn是第n簇到达时间，τnk是第n簇中第k条路径的时延，二者都服从泊松分布。另外，多径平均功率成双指数衰减模型

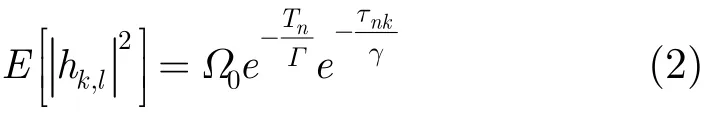
其中E[.]表示统计平均，Ω0为首达径的平均功率，Γ为簇到达率，γ为径到达率。IEEE 802.15.3a工作组确定了4种标准UWB信道模型CM1-CM4，4种模型的上述变量的分布参数不同，其中CM4信道最为恶劣，如表1所示[8]。

表1 UWB-OFDM信道模型参数

3 本文提出的定时同步方法

3.1 帧检测及粗定时

本文参照文献[3]所述的自相关方法，但相关窗长度的选择不同，并且粗定时后需要对定时位置进行修正来为细定时做铺垫。接收机在帧检测及粗定时之前不启动解跳频，下变频的本地振荡器初始于第1频带中心频率上。利用第1频带的前两个同步符号进行帧检测及粗定时，然后根据定时位置启动解跳频。

帧同步利用第1子频带的前两个训练符号，进行自相关检测，

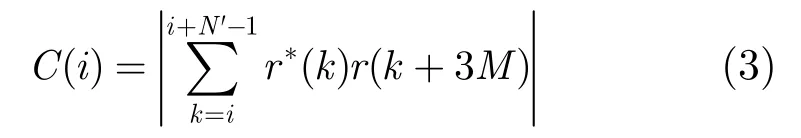
其中M=165为符号长度，i=1,2,…为采样点序号，N'为相关窗口长度。仿真确定一门限值G，当连续3个C(i)大于G时，确认为检测到了帧，设此时对应的i=μ。然后进行粗定时，在i∈[μ, μ+M]范围内找C(i)的最大值，并将此最大值对应的位置ict定为粗定时同步位置。

设正确的定时位置为T，定义定时偏差为

为避免由于ZP造成的自相关峰出现平坦区域，N'取128，本文第4节的仿真表明与文献[3]的132相比具有更好的相关峰。

假设在某一信道模型CMi下粗定时偏差范围为di∈[ai,bi]，i=1, 2, 3, 4。若要使用OLA均衡方法对定时偏差进行补偿，需要定时偏差di∈[-(Ng-Li), 0]，其中Ng=37，不同信道模型下的多经数见表1。本文对粗定时位置做−δct的修正，使不出现定时滞后的情况，则修正后的定时同步位置为

其中δct为粗定时的最大滞后长度为

则定时偏差为

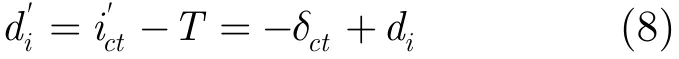
另外，式(3)的自相关需要进行N'次复数乘法和N'-1次复数加法运算，即4N'次实数乘法和4N'-2次实数加法，式(4)需要进行M次比较运算，可以看出N'的大小会影响算法复杂度。

3.2 细定时同步

粗定时后启动解跳频，利用3个频带信息进行细定时。本文参照文献[8]所述的盲同步方法，并在此法基础上进行改进，使之适用于多频带系统，并给出能量比值的滑动比较范围。细定时基于前导序列中每个频带的第3个符号，利用系统保护间隔为零的特点，来做两连续滑动窗口能量的比，在一定范围内找最小能量比值确定符号起始位。

其中H为能量窗口长度，q为频带序号，分子表示3个频带前一窗口能量和，分母表示3个频带相邻后一窗口能量和。为保持较低复杂度，可以不估计信道多径数L，而是根据经验选择一个较大的L，从而窗口长度H小于等于Ng-L即可。寻找最小能量比值的范围由粗定时结果决定，令γ=min(ai)，可知修正后在所有UWB信道模型下的总的粗定时偏差范围为d'∈[ai-δct, 0]，则在i∈[,+δct−γ]范围内对能量比值进行比较找出最小值从而确定细定时同步位置ift。

此细定时方法所确定的最小能量窗比值的位置是ZP和OFDM数据符号的相邻处，即符号起始位置。所以粗定时后的解跳频必须基于修正后的粗定时位置，即不能出现滞后解跳的情况。否则，由于错误解跳的部分会被匹配滤波器滤掉，符号的滞后解跳造成OFDM符号的开头数据被滤除，相当于开头数据近似变成ZP，则最小能量窗比值的位置将滞后，细定时性能无法得到保证。而若定时超前，匹配滤波滤掉的错误解跳频的部分为OFDM符号的末尾数据，最小比值位置不受影响。

在细定时后，用与粗定时同样的方法对定时偏差做修正，使不会出现定时滞后的情况，以便使用OLA法进行频域信道均衡来联合补偿信道及残余定时偏差。二次修正后的定时位置为

其中δft为细定时最大滞后偏差，其值由仿真来确定。此外，该同步方法是对某一窗口求能量，即求模方，与相位无关，所以此法不受载波频偏的影响，即对频偏不敏感。

上面说的最小能量窗比值法基于单个符号，可以改进为先对连续多个符号的多个窗口求能量和，再求其比值，以进一步提高性能。其能量比值表示如下：

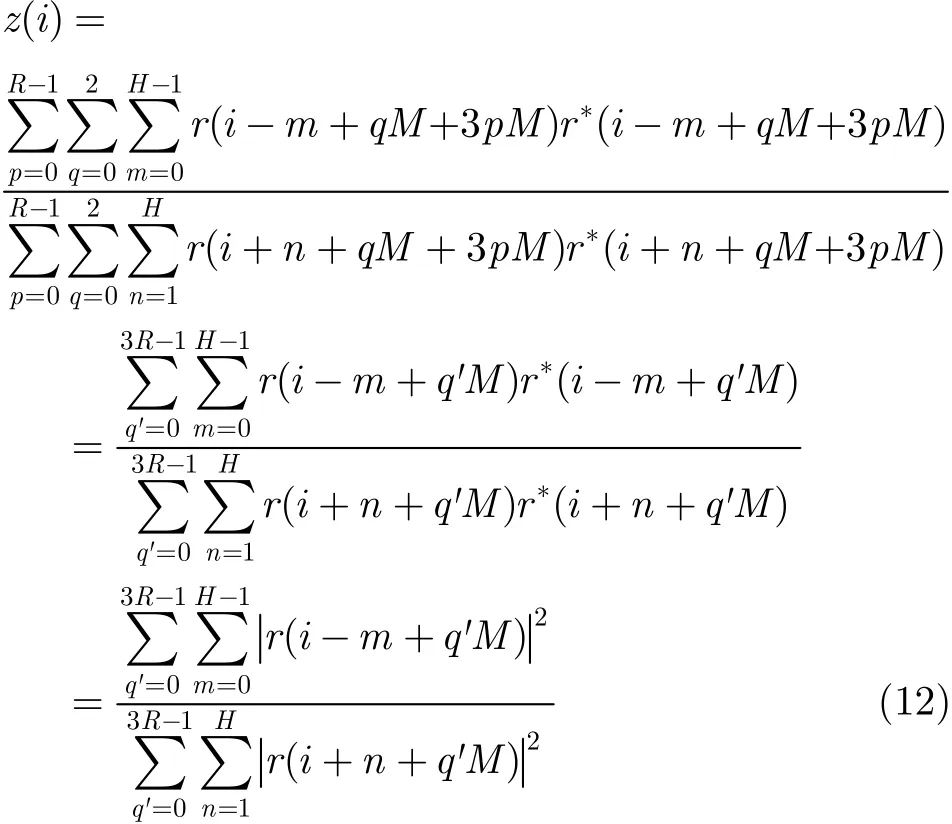
其中R为所用的每个频带的符号数。根据该比值确定定时位置的方法同式(10)。

下面分析一下细定时算法的运算量，R个符号下，式(12)需要进行12RH次实数乘法运算，12RH-2次实数加法运算及1次实数除法运算。式(10)需要进行δct−γ次比较运算。可以看出，能量窗口长度H及符号个数R会影响算法复杂度。

4 性能仿真

对ECMA-368规定的UWB系统进行仿真，信道时变，其参数设为每帧变化一次。如图3所示为帧检测和粗同步中的相关值C(i)，可以看到窗口长度N'为128对应的相关峰十分尖锐，其最大相关值对应横坐标为5949，即粗定时位置唯一。而文献[8]采用的132会使相关峰出现平坦区域，即最大相关值对应的横坐标是一段区域[5945,5949]，这样即使没有任何干扰的情况下，粗定时位置也会出现误差，粗定时性能受到影响，而且N'为128时的运算量相对较低。图4为信噪比为0 dB，CM4信道下，N'取128时，不同门限值G对应的虚警和漏警概率，可以看出G取0.35～0.5时性能最佳。

图5为AWGN，CM1-CM4信道下信噪比为0 dB，N'取128，G取0.425时的粗定时偏差概率图。可以看出CM4信道下定时性能最差，偏差最大。其最大超前偏差为2，最大滞后偏差为32，则修正值δct=32。容易看出几种信道模型下均不能满足对于所有都属于[-(Ng-Li), 0]。例如，在CM4信道下，d∈[9,32]，修正后，∈[-23, 0]。由表1，L=26，

图3 帧检测和粗同步中的自相关峰

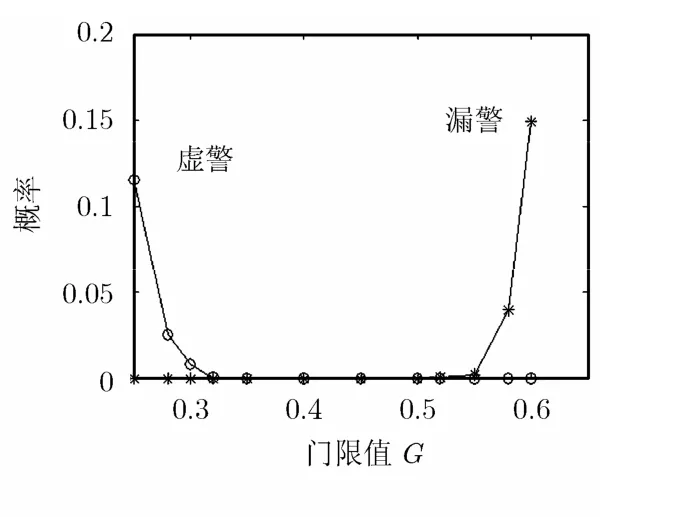
图4 不同门限下的虚警和漏警概率

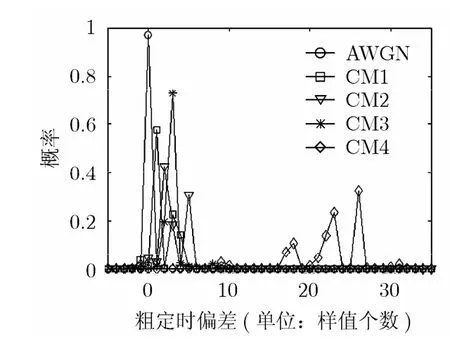
图5 不同信道模型下的粗定时偏差概率

图6 不同能量窗长度下的细定时均方根误差曲线

图7 不同符号数下的细定时均方根误差

44[-(Ng-L4), 0]=[-11,0]。[-23,0]不属于[-11,0]，故OLA法无法纠正；在CM1信道下，d1∈[-1，8]，修正后，∈[-33,-24]，由表1，L1=8，[- (Ng-L1),0]=[-29,0]。[-33,-24]不属于[-29,0]，OLA法同样无法纠正。所以需要细定时，细定时比较范围为[,+34]。为保持较低复杂度，不估计信道多径数，而是根据经验选择一个较大的多径数26，则能量窗长度H小于等于11。图6为CM4信道下，能量窗口长度为5，6，8，10和11时的细定时偏差的均方根误差(MSRE)曲线。可以看出，12 dB时不同窗口长度的MSRE均小于2。另外，并不是窗口越大效果就越好，信噪比较高时不同长度窗口性能相近，信噪比较低时窗口长度的增加也不会使性能提高。所以，考虑到复杂度，应该选用较小的H。图7为CM4信道下、窗口长度为5时，利用单个符号和多个符号求能量比值的MSRE曲线，其分别为采用前导序列的第3个符号、第3至第6个符号以及第3至第8个符号。可以看到，9 dB时不同符号数下的MSRE均小于2，并且符号数越多定时性能越好，因为利用多个符号可以起到平滑噪声的作用。在信噪比较低时，符号数的增加会使性能有很大提升，信噪比越高，性能提高就越不显著。所以，如果系统应用在信噪比较好的环境中，那么可以选择符号数R较小以降低复杂度；如果环境恶劣或时好时坏，那么应该使R较大，以复杂度的增加换取性能的提高。

通过上述仿真，综合考虑到实现复杂度，我们最终确定能量窗口长度为5，利用前导序列的第3至第8共6个同步符号进行细定时。图8为AWGN，CM1-CM4信道下信噪比为0 dB时的细定时偏差概率图。可以看到，细定时的最大滞后偏差为3，则修正δft=3，容易看出这样能够保证在所有信道模型CM1-CM4下，二次修正后的细定时偏差均落在[-(Ng-Li), 0] 内。至此我们达到了预期目标，残余的定时偏差可以被频域信道均衡所吸收。

图8 不同信道模型下的细定时偏差概率线

5 结论

本文针对IEEE 802.15.3a提案及ECMA-368标准采用的多频带OFDM超宽带系统，通过算法改进和仿真给出了适用于该系统的定时同步的完整方案。用基于前导序列第1频带信息的最大自相关法进行帧检测及粗定时，用基于全部3个频带信息的最小能量比值法进行细定时，同时对粗细定时位置先后两次进行修正。该方案兼顾了定时同步性能与系统实现复杂度，用复杂度较低的算法来实现对定时偏差的有效纠正，残余的定时偏差可以在频域被信道估计及均衡吸收。

[1] IEEE Std. Multi-band OFDM physical layer proposal for IEEE 802.15 Task Group 3a[S]. 2004.

[2] ECMA Std. High rate ultra wideband PHY and MAC standard[S]. 2005.

[3] 李平，赵志辉，张振仁. OFDM系统建模仿真及同步偏差分析[J]. 系统仿真学报，2007, 19(13): 3042-3046.Li Ping, Zhao Zhi-hui, and Zhang Zhen-ren. Simulation of OFDM system model and synchronization errors analysis[J].Journal of System Simulation, 2007, 19(13): 3042-3046.

[4] Wang Yue and Dong Xiao-dai. Comparison of frequency offset and timing offset effects on the performance of SC-FDE and OFDM over UWB channels[J]. IEEE Transactions on Vehicular Technology, 2009, 58(1): 242-250.

[5] Minn H, Bhargava V, and Letaief K. A robust timing and frequency synchronization for OFDM systems[J]. IEEE Transactions on Wireless Communications, 2003, 2(4):822-839.

[6] Minn H, Bhargava V, and Letaief K. A combined timing and frequency synchronization and channel estimation for OFDM[J]. IEEE Transactions on Communications, 2006,54(3): 1081-1096.

[7] Berger C R, Zhou Sheng-li, and Tian Zhi, et al.. Performance analysis on an MAP fine timing algorithm in UWB Multiband OFDM[J]. IEEE Transactions on Communications, 2008, 56(10): 1606-1611.

[8] 李长青，刘丹谱，乐光斯. UWB-OFDM系统的符号盲同步方法[J]. 电子与信息学报，2007, 29(8): 1895-1899.Li Chang-qing, Liu Dan-pu, and Yue Guang-xin. A robust blind symbol-timing synchronization for UWB-OFDM systems[J]. Journal of Electronics & Information Technology,2007, 29(8): 1895-1899.

[9] Li Y, Minn H, and Rajatheva R M A P. Synchronization,channel estimation, and equalization in MB-OFDM Systems[J]. IEEE Transactions on Wireless Communications,2008, 7(11): 4341-4352.

[10] Muquet B, Wang Z, and Giannakis G, et al.. Cyclic prefixing or zero padding for wireless multicarrier transmisions?[J].IEEE Transactions on Communications, 2002, 50(12):2136-2148.