基于网络编码的分层媒体多播中的层速率分配优化

林晓斌 许胤龙 詹 成 王青山

①(中国科学技术大学计算机科学与技术学院 合肥 230027)②(安徽省高性能计算重点实验室 合肥 230027)③(合肥工业大学理学院 合肥 230009)

1 引言

随着网络技术的快速发展，视频会议、远程教学、交互视频游戏等众多流媒体应用受到广泛的关注。由于网络的异构性，同一个多播会晤中各接收节点可能具有不同的接收带宽。单速率多播中，所有接收节点以相同速率接收服务，不适合异构网络。而多速率多播在同一个多播会晤中以不同的速率为不同接收节点提供服务，更适合大规模异构网络的多媒体应用。

分层多播(累积分层多播)[1]是一种广泛应用的多速率多播技术。在分层多播中，源节点将多媒体数据编码成一个基础层和若干增强层。基础层包含最基本数据，能够独立解码；而增强层k只有在基础层，增强层1，增强层2，…，增强层k−1都收到时才能解码。接收节点收到的分层数量越多服务质量越好。各接收节点可以根据各自的带宽接收相应层数的分层数据。

在传统的网络通信中，中间节点收到数据后对数据不进行任何处理，只实现存储转发。而利用网络编码(network coding)[2]，中间节点对收到的数据进行编码处理后再转发，接收节点收到足够的编码数据后，通过解码操作即可得到所有参与编码的原始数据。通过网络编码，中间节点可以增加每次传输的有效信息量，从而提高网络吞吐量。Ahlswede等人[2]、Koetter等人[3]证明了利用网络编码多播组可以达到的最大多播速率等于源节点到各接收节点的最大流的最小值。Li等人[4]证明了利用线性网络编码多播组就可以达到最大多播速率。Sanders等人[5]则提出了构造线性编码的多项式时间算法来保证多播组能达到最大多播速率。

近年来，基于网络编码的多速率媒体多播引起了一些专家学者的关注。文献[6-9]研究了多速率多播的问题，但没有考虑分层之间的优先级，不符合分层多播中高层数据依赖低层数据解码的特性。在每层速率已知的前提下，Zhao等人[10]、Xu等人[11]、Wu等人[12]分别研究了基于网络编码的分层多播。由于这些工作都假定各层速率是预先固定的，不能根据网络拓扑动态分配各层速率，从而不能充分利用网络带宽。在层速率可变的假定下，Zhang等人[13]研究了基于网络编码的层速率分配问题。由于该问题是一个非线性整数规划的问题，他们提出了确定层速率的近似算法ApproxIVM。但该算法根据少数最大流较小的接收节点的最大流来确定层速率，会导致多数最大流较大的接收节点不能充分利用带宽；且每一分层速率确定后，文中没有给出算法用于分配每层数据所需的链路带宽，从而不能充利用网络带宽。

针对每层速率可变的分层多播问题，本文研究了基于网络编码的层速率优化分配算法。该算法首先将网络图按接收节点的总数分解成子图，然后将这些子图按分层层数进行合并，在合并后的各子图中接收节点的最大流的最小值即是优化分配的各层速率大小。相比低带宽接收节点优先的层速率分配算法ApproxIVM[13]，本文的算法居于全局优化，能够满足不同接收节点的带宽需求。模拟实验表明本文算法能够显著提高网络吞吐量，提高网络带宽的利用率。

2 问题模型

本节对基于网络编码的分层媒体多播中的层速率分配优化问题进行简要的形式化描述。表1给出几个重要的变量。

将网络用有向图G(V, E, s, T)表示，其中V是节点集，E是边集，s是源节点，T是所有n个接收节点的集合，即T={t1, t2,…,tn}⊆V 。边(u, v)表示节点u和节点v之间的链路，c(u, v)表示链路(u, v)的容量。假定s上的视频数据经编码器分层编码后形成m(m≤n)个具有顺序关系的层：第1层(基础层)，第2层(增强层1)，…，第m层(增强层m−1)。为保证各接收节点能够正确地解码接收的网络编码数据包，本文限定对分层编码的视频文件进行网络编码时只是在同一分层的数据包之间进行。因为如果允许不同分层的数据包之间进行网络编码，可能造成低带宽的接收节点由于只能接收部分的网络编码包，从而不能正确解码。

表1 模型的部分变量

由文献[11,13]，基于网络编码的分层媒体多播中的层速率优化分配问题可模型化为以下数学规划：

数学规划的目标是最大化各接收节点的接收速率总和，即网络吞吐量。约束条件(1)和条件(2)是分层媒体数据的解码条件，即第k层在第1层到第k−1层都接收的前提下才能解码。约束条件(3)是从源节点s到每一特定接收节点ti(∀ti∈T)的第k(∀k=1,2,…,m)层的数据流的平衡条件。约束条件(4)是基于网络编码的带宽使用特性：同一层数据流之间不竞争链路带宽。约束条件(5)保证每条链路的带宽使用在其容量限制之内。

3 启发式算法

在分层媒体多播中，网络各链路为每层数据分配链路带宽。根据各链路为m层数据分配的链路带宽，网络图G (V, E, s, T)被分解成m个子图Gk(Vk, Ek,s, Tk)(1≤k≤m)。Gk(Vk, Ek, s, Tk)是第k层数据在网络G (V, E, s, T)中的传输图，其中Ek={(u, v)|fk(u, v)＞0,(u, v)∈E}，V为与E中的边关联的节点集合, Tk是接收第k层的接收节点集合。在层速率固定(即在问题模型的数学规划中，bk是已知常量，此时数学规划为整数线性规划)的情形下，文献[13]证明了数学规划的可行解对应于将网络图分解的各子图中的各参数，文献[10,11]设计了相应的算法根据给定的各层速率将网络图分解成子图。而在层速率可变(即在问题模型的数学规划中，bk是需优化的变量，此时数学规划为非线性整数规划)的情形下，本文通过证明定理1从而求解各层的优化速率并得到各层相应的传输子图。

定理1 在图G(V, E, s, T)按最大化吞吐量最优分解的m个子图Gk(Vk, Ek, s, Tk)(1≤k≤m)中，从s到Tk的各接收节点最大流的最小值minmaxflow(Gk)是第k层的最优层速率。

证明 不妨设在传输子图Gk(Vk, Ek, s, Tk)中从s到ti(ti∈Tk)的最大流maxflow(ti)=min-maxflow(Gk)。若min-maxflow(Gk)＜，则ti不能收到第k层，即ti∉Tk，矛盾。若min-maxflow(Gk)＞，利用算法LIF[5]设定网络编码系数，对在子图Gk(Vk,Ek, s, Tk)中传输的数据包进行网络编码，能够保证Tk中的所有接收节点都以min-maxflow(Gk)接收数据，与题设是第k层的最优层速率矛盾。因此，min-maxflow(G)=。 证毕

由定理1，优化分配m层的层速率即是将网络图优化分解成m个传输子图，每个传输子图中从源到各接收节点的最大流的最小值即是优化的层速率。由于直接将网络图分解成m(m≤n)个子图较困难，本文先设计算法NRAA(N-layer Rate Allocation Algorithm)将网络图按接收节点的个数n分解成n个传输子图Hl(Vl, El, s, Tl)(1≤l≤n)，其中E={(u, v)|yl(u, v)＞0,(u, v)∈E}且yl(u, v)表示n层机制下链路(u, v)为第l层分配的带宽，Vl是与El中的边相关联的节点集合，Tl是接收n层机制下第l层的接收节点集合；然后设计算法MRAA(M-layer Rate Allocation Algorithm)将n个子图Hl(Vl, El, s, Tl)(1≤l≤n)合并成m个子图Gk(Vk,Ek, s, Tk)(1≤k≤m)，在合并而成的各子图中接收节点最大流的最小值即是优化分配的m层机制下的各层速率。

3.1 算法NRAA

将图G (V, E, s, T)分解成n个子图，则每个接收节点都能按照各自的接收带宽接收分层数据。假定图Rl(Vl, El, s, Tl)是网络图G (V, E, s, T)为n层机制下的第1层到第l−1(2≤l≤n)层分配链路带宽后的残余图。由定理1，我们可根据图Rl(Vl, El, s, Tl)中从s到Tl的各接收节点的最大流来确定n层机制下第l层速率，并设计如下算法NRAA：如果所有接收节点的最大流都大于0，则以最大流的最小值为第l层速率，各链路为第l层优化分配链路带宽以构造传输子图Hl(Vl, El, s, Tl)(1≤l≤n)。否则如果最大流等于0的接收节点个数δ≥1，则删除当前最大流为0的全部接收节点并确定第l层到第l+δ−1层的速率为0，即本文允许空层的存在。重复上述操作，直至n层机制下各层速率和各层传输子图都得以确定。在算法NRAA构造的各层传输子图Hl(Vl,El, s, Tl)(1≤l≤n)中利用算法LIF[5]作为网络编码方案，能够保证Tl中的所有接收节点都能以图Hl(Vl, El, s, Tl)中从s到Tl的各接收节点的最大流的最小值作为接收速率接收n层机制下的第l层数据。

算法NRAA与算法ApproxIVM[13]有些相似，但不同的是：算法ApproxIVM是通过m(m≤n)次迭代地取残余图中的非零最大流的最小值来确定m层机制下的各层速率；且对于层速率优化的关键部分(即层速率确定后如何优化分配为满足该层速率所需的链路带宽)，算法ApproxIVM没有给出相应的链路带宽分配策略，从而直接影响下一层速率的大小，本文则在算法NRAA中提出如下启发式算法NALBA(New Algorithm for Link Bandwidth Allocation)为第l(1≤l≤n)层数据优化分配链路带宽，进而从残余图Rl(Vl, El, s, Tl)中优化分解出n层机制下第l层传输子图Hl(Vl, El, s, Tl)。

因为本文以图Rl(Vl, El, s, Tl)中从s到Tl的各接收节点的最大流的最小值为第l层速率，所以图Rl(Vl, El, s, Tl)中最大流最小的接收节点的路径带宽全部分配给第l层数据。因此，在非最小最大流的接收节点的各路径上为第l层数据分配带宽时，应让它们充分利用最大流最小的接收节点路径上为第l层数据必需分配的带宽。根据此思想，算法NALBA详细过程如下：

在图Rl(Vl, El, s, Tl)中，根据算法Edmonds-Karp[14]计算从s到ti(ti∈Tl)的最大流maxflow(ti)，并找出最大流经过的路径集合Pi。假设maxflow(ti)经过路径的流量是，经过链路(u, v)的流量是Fi(u, v)。令表示Tl中最大流最小的接收节点集合。确定Tl中接收节点的最大流的最小值min为第l层速率。要使中的所有接收节点都能接收第l层数据，则在链路(u, v)上需分配的带宽f'(u, v)=max{Fi(u, v)|ti∈}。对最大流大于min的每个接收节点ti(ti∈Tl−)，都分别执行如下各步骤为第l层分配链路带宽(表2)。

表2 第l层分配链路带宽

表2中第(3)步对均匀分摊网络带宽到各路径的处理方法，可参见文献[10]的Heuristic Approach。在算法NALBA中，路径为从s到ti(ti∈)的第l层数据分配的带宽=，路径为从s到ti(ti∈Tl−)的第l层数据分配的带宽=preFlo+evenFlo。n层机制下链路(u, v)上为通往ti(ti∈Tl) 的第l层数据分配的带宽：

因此，n层机制下链路(u, v)为第l(1≤l≤n)层数据分配的总带宽为

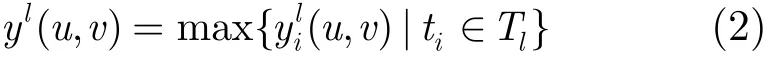
证明 算法NALBA对所有接收节点执行相同操作，所以我们以单个接收节点ti(ti∈Tl)为例进行分析。不妨设ti为非最小最大流的接收节点。首先执行算法Edmonds-Karp[14]计算maxflow(ti)并找出ti的路径集Pi，时间复杂度为O(| Vl||El|2)。其次，算法NALBA为第l层分配链路带宽各步骤的时间复杂度为O(|El|)。综上，对单个接收节点ti所需执行操作的时间复杂度为O(| Vl||El|2)+O(|El|)=O(| Vl||El|2)。共有|Tl|个接收节点，因此算法NALBA的时间复杂度为O(| Tl||Vl||El|2)。 证毕

基于算法NALBA分配n层机制下各层传输子图的链路带宽，本文设计算法NRAA如表3所示：

表3 本文设计算法NRAA

在算法NRAA构造的图Hl(Vl, El, s, Tl)(1≤l≤n)中利用算法LIF[5]作为网络编码方案，能够保证Tl中的所有接收节点都接收到n层机制下的第l层数据。

由算法NRAA优化分配n层机制下的层速率列表A=＜a1, a2,…,an＞，并得到n层机制下各接收节点的接收速率列表C=＜c1, c2,…,cn＞，则根据算法NRAA的设计思想显然易证以下性质。

性质1 若由算法NRAA得到的各接收节点的接收速率c1, c2,…,cn满足c1≤c2≤…≤cn，则ci(1≤i≤n)与n层机制下各层速率a1, a2,…,an之间的关系满足ci=a1+a2+…+ai。

定理3 在网络G (V, E, s, T)中，n(|T|=n)层机制下的层速率优化分配算法NRAA的时间复杂度为O(| V||T|2|E|2)。

证明 算法NRAA的时间复杂度是由n次调用算法NALBA决定的。而由定理2，在网络G (V, E,s, T)的残余子图Rl(Vl, El, s, Tl)中，算法NALBA的时间复杂度为O(| Tl||Vl||El|2)，其中Vl⊆V, El⊆E, Tl⊆T。所以算法NRAA的时间复杂度为n*O(| T||V||E|2)=O(| V||T|2|E |2)。 证毕

3.2 算法MRAA

为优化分配m(m≤n)层的层速率，本文将由算法NRAA预先分成的n层视频数据合并成m层。假定由算法NRAA优化分配的n层机制下层速率列表A=＜a1, a2,…,an＞，接收节点接收速率的有序列表C=＜c1, c2,…,cn＞(其中c1≤c2≤…≤cn)。在最大化网络吞吐量的目标下，将n层合并成m层的过程等价于在最大化的目标下，将有序列表C划分成m个子列表C1, C2,…,Cm。其中|Ck|表示子列表Ck的元素个数，min(Ck)表示子列表Ck中的最小值。上述划分即是将n个接收节点划分成m个接收组Q1, Q2,…,Qm，在接收组Qk中有|Ck|个接收节点且组中的所有接收节点都能以速率min(Ck)接收在m层机制下从第1层到第k层的共计k层的分层数据。因此可优化分配m层机制下各层速率为

对于有序列表划分成子列表的问题，Gau等人[15]证明了有序列表的最优划分一定是有序划分，并提出了把元素个数为n的有序列表划分成m个有序子列表的多项式时间算法FALP(Fast Algorithm for List Partition)。

不妨设有序列表C=＜c1, c2,…,cn＞(其中c1≤c2≤…≤cn)，经算法FALP划分成有序子列表(每个子列表的元素从小到大排序)为：C1=＜c1, c2,…,ci1−1＞(注：i0=1),C2=＜ci1,ci1+1,…,ci2−1＞,…,Cm=＜cim−1,cim−1+1,…cn＞，则接收节点集合T={t1, t2,…,tn}被分成的m个接收分组：

因此，m层机制下，Tk=Qi。在组Qk(1≤k≤m)中的接收节点的接收速率都为cik−1，又根据式(3)，优化分配m层机制下各层速率为

而由算法NRAA的性质1：ci=a1+a2+…+ai(1≤i≤n)，因此优化分配m层机制下第k(1≤k≤m)层速率为

即m层机制下的第k(1≤k≤m)层数据是由n层机制下的第ik−2+1层到第ik−1层共ik−1−ik−2层数据合并而成的。因此m层机制下第k(1≤k≤m)层的传输子图Gk(Vk, Ek, s, Tk)的链路带宽fk(u, v)与n层机制下的各传输子图Hl(Vl, El, s, Tl)(1≤l≤n)的链路带宽yl(u, v)满足以下等式：

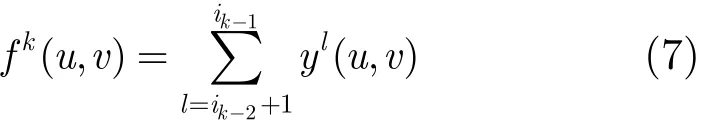
综上，本文设计算法MRAA将算法NRAA构造的n层机制下的n个传输子图合并成m个传输子图，优化分配m层机制下的各层速率。算法MRAA如表4所示。

表4 本文设计算法MRAA

在算法MRAA构造的第k(1≤k≤m)层传输子图Gk(Vk, Ek, s, Tk)中，利用算法LIF[5]作为网络编码方案，能够保证Tk中的所有接收节点都能以式(6)所示的速率接收m层机制下的第k层数据。

定理4 在网络G (V, E, s, T)中，m(m≤n=|T|)层机制下的层速率分配算法MRAA的时间复杂度为O(| V||T|2|E|2)。

证明 算法MRAA由3步组成。第1步，调用算法NRAA，时间复杂度为O(| V||T|2|E|2)；第2步，按接收速率排序结果对接收节点重新编号，时间复杂度为O(n2)=O(| T|2)；第3步，调用算法FALP，时间复杂度为O(mn2)=O(m| T |2)。所以总时间复杂度为O(| V||T|2|E|2)+O(| T|2)+O(m| T|2)=O(| V||T|2|E |2)。 证毕

4 模拟实验

本文通过C++模拟实验进行算法性能评价。首先比较为各层视频数据分配链路带宽的新算法NALBA、随机分配策略RANDOM、算法Heuristic Approach[10]的均匀分配策略；然后比较层速率全局优化分配算法MRAA、低带宽接收节点优先的层速率分配算法ApproxIVM[13]、层速率固定的算法Heuristic Approach[10]。

文献[16]表明为满足网络的异构性并保持合理的额外开销，在分层多播中分层层数为4层是较为合理的值。因此本文在实验中取分层层数m=4。

在应用网络编码的前提下，从源节点到某特定接收节点的最大流的值反映该接收节点的可接收带宽的大小。在实验中本文先采用平均标准化接收速率ANR(Average Normalized Rate)[6]如式(8)所示(其中ri表示ti接收到的各分层数据的总速率，maxflow(ti)表示从s到ti的最大流，T是所有接收节点的集合。)对各算法进行比较。参数ANR反映网络中各接收节点对各自可接收带宽的平均利用率。参数ANR越大，表明各接收节点的实际接收带宽越趋近各自的可接收带宽。但是本文的优化目标是吞吐量，因此本节定义标准化的总接收速率NTR(Normalized Total Rate)如式(9)所示(式(9)中各变量与式(8)含义一致。)来表示整个网络的实际接收带宽总和占可接收带宽总和的比例，反映整个网络的带宽使用总量，即网络吞吐量。

4.1 参数ANR比较实验

图1采用50个节点和10个接收节点的随机网络拓扑。在算法MRAA的步骤1，即执行算法NRAA时，分别执行随机分配路径带宽的RANDOM策略，算法Heuristic Approach的均匀分配策略和算法NALBA 3种不同的方案为每层数据分配链路带宽，得到算法MRAA的3个不同结果。图1中RANDOM策略最差。因为RANDOM策略在各路径上为每层数据随机分配带宽，没有考虑带宽的有效分配。在图1中，当网络的节点平均度从5增加到8时，算法NALBA相比算法Heuristic Approach的均匀分配策略对ANR参数的改进在图1(a)中由3%增加到7%，在图1(b)中由5%增加到10%。这是因为节点度越大，从源节点到不同接收节点的路径之间有公共链路的可能性越大，所以算法NALBA在非最小最大流的接收节点的路径上为各层分配带宽时，让那些与最大流最小的接收节点的路径有公共链路的路径共享最小最大流接收节点的路径上为该层视频数据必需分配的带宽能够节省更多的带宽。

图2采用100个节点，接收节点个数在[4,40]以步长为4变化，链路容量均匀分布在[1,20]的随机网络拓扑。图2是算法MRAA，算法ApproxIVM，算法Heuristic Approach的比较结果。其中在层速率固定的算法Heuristic Approach中，本文假定从源节点到各接收节点的最大流的范围已知为[Min,Max]，源节点根据此范围固定第1层的速率为Min，其他层的速率相等且为(Max−Min)/(m−1)，m为分层层数。从图2中可以看出，MRAA相比ApproxIVM和Heuristic Approach对ANR参数的改进在图2(a)中平均分别为6%和20%，在图2(b)中平均分别为10%和19%。因为MRAA根据网络拓扑从全局的角度优化分配各层速率，并且采用算法NALBA为各层有效分配链路带宽；ApproxIVM只根据网络中最大流最小的4个接收节点的最大流来确定4层视频数据的速率而且在各链路为每一层数据分配带宽时采用随机分配的方式，这些都使得网络ANR参数受影响；而Heuristic Approach中各层速率固定，没有根据网络拓扑分配各层速率，因此其ANR参数最差。

4.2 参数NTR比较实验

图1 NALBA, RANDOM, Heuristic Approach算法的参数ANR比较

图2 MRAA, ApproxIVM, Heuristic Approach算法的参数ANR比较

图3 NALBA, RANDOM, Heuristic Approach的参数NTR比较

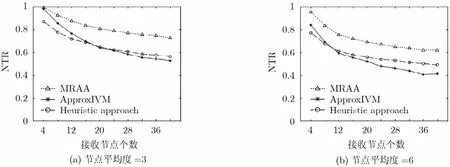
图4 MRAA, ApproxIVM, Heuristic Approach的参数NTR比较

当以NTR为比较参数时，重复上述实验得到实验结果如图3和图4。图3与图1相似，而图4与图2相比有些变化。在图4中，MRAA相比Heuristic Approach和ApproxIVM对网络吞吐量的提高在图4(a)中平均分别为16%和15%，在图4(b)中平均分别为14%和18%。因为MRAA考虑全局最优，使得所有接收节点都能充分利用带宽，所以各接收节点的平均带宽利用率和网络吞吐量都是三者中最优的。在图4(a)和图4(b)中，随着接收节点个数的增加，层速率固定的算法Heuristic Approach的吞吐量反而大于层速率经部分优化分配的算法ApproxIVM。因为本文设定Heuristic Approach根据接收节点最大流的范围固定各层速率；而ApproxIVM根据少数低带宽接收节点的最大流分配各层速率，从而导致多数最大流较大的高带宽接收节点只能以低速率接收分层数据，不能充分利用带宽，从而影响网络吞吐量，尤其是当接收节点较多时。

5 结束语

本文研究了基于网络编码的分层媒体多播中的层速率分配优化问题。证明了将网络图按分层层数最优分解成的各网络子图中的接收节点的最大流的最小值即是各层的最优层速率，并根据此思想提出了时间复杂度为O(| V||T|2|E|2)的启发式算法MRAA优化分配各层速率。模拟实验表明本文的算法能够显著改善网络吞吐量，提高各接收节点的平均带宽利用率。本文的研究工作基于单会晤多播的情形，而在多会晤情形下基于网络编码的分层媒体多播中的层速率分配优化问题要复杂得多，我们将以此作为将来进一步的研究工作。

[1] McCanne S, Jacobson V, and Vetterli M. Receiver-driven layered multicast. Proc. of ACM SIGCOMM 1996, Stanford,CA, USA, Aug. 1996: 117-130.

[2] Ahlswede R, Cai N, and Li S R, et al.. Network information flow. IEEE Transactions on Information Theory, 2000, 46(4):1204-1216.

[3] Koetter R and Medard M. An algebraic approach to network coding. IEEE/ACM Transactions on Networking, 2000, 11(5):782-795.

[4] Li S R, Yueng R W, and Cai N. Linear network coding. IEEE Transactions on Information Theory, 2003, 49(2): 371-381.

[5] Sanders P, Egner S, and Tolhuizen L. Polynomial time algorithms for network information flow. Proc. of the 15th Annual ACM Symposium on Parallel Algorithms and Architectures (SPAA), San Diego, CA, USA, June 2003:286-294.

[6] Sundaram N, Ramanathan P, and Banerjee S. Multirate media stream using network coding. Proc. of the 43rd Allerton Conference on Communication, Control, and Computing, Monticello, IL, USA, Sep. 2005.

[7] Wu X, Ma B, and Sarshar N. Rainbow network problems and multiple description coding. IEEE Transactions on Information Theory, 2008, 54(10): 4565-4574.

[8] Shao M, Wu X, and Sarshar N. Rainbow network flow with network coding. Proc. of NetCod 2008, Hong Kong, China,Jan. 2008: 1-6.

[9] Shao M, Dumitrescu S, and Wu X. Toward the optimal multirate multicast for lossy packet network. Proc. of ACM Multimedia 08, Vancouver, BC, Canada, Oct. 2008: 765-768.[10] Zhao J, Yang F, and Zhang Q, et al.. LION: Layered overlay multicast with network coding. IEEE Transactions on Multimedia, 2006, 8(5): 1021-1032.

[11] Xu C, Xu Y, and Zhan C, et al.. On network coding based multirate video streaming in directed network. Proc. of the 26th IPCCC, New Orleans, Louisiana, USA, Apr. 2007:332-339.

[12] Wu Y. Distributing layered content using network coding. 5th IEEE Annual Communications Society Conference on Sensor,Mesh and Ad hoc Communications and Networks Workshops,San Francisco, CA, USA, June 2008: 1-4.

[13] 张牧, 张顺颐, 刘伟彦. 多速率多播最大吞吐量问题研究. 电子与信息学报, 2008, 30(1): 16-20.Zhang M, Zhang S, and Liu W. On the optimal multi-rate throughput for multicast. Journal of Electronics &Information Technology, 2008, 30(1): 16-20.

[14] Cormen T H, Leiserson C E, and Rivest R L, et al..Introduction To Algorithms (Second Edition). Massachusetts:MIT Press, 2001: 643-698.

[15] Gau R, Haas Z J, and Krishnamachari B. On multicast flow control for heterogeneous receivers. IEEE/ACM Transactions on Networking, 2002, 10(1): 86-101.

[16] Yang Y R, Kim M S, and Lam S S. Optimal partitioning of multicast receivers. Proc. of ICNP 2000, Osaka, Japan, Nov.2000: 129-140.