基于奇异值分解更新的多元在线异常检测方法

钱叶魁 陈 鸣

①(解放军理工大学指挥自动化学院 南京 210007)②(解放军防空兵指挥学院 郑州 450052)

1 引言

所谓网络异常是指网络运行偏离正常状态的情况。导致网络异常的原因很多，包括网络设备误配置、网络故障、网络安全事件(分布式拒绝服务攻击、蠕虫传播等)以及不寻常的用户行为等。异常检测对于保证网络的正常运行具有重要意义，一直是网络研究的热点问题。

Lakhina等人[1,2]提出的基于PCA的异常检测算法奠定了多元异常检测的基础。Jin等人[3]运用流量活动图分解的方法对骨干网流量进行了分析，揭示了各种网络异常行为；Torres等人[4]运用流量聚类的分析方法推断P2P网络的异常行为。这些方法都是一种离线的分析方法，无法适用于在线分析和检测异常的需要。而现有的网络异常在线检测算法[5]大都仅仅关注单条链路的流量异常或单条端到端路径的性能异常。国内有关网络流量异常检测的文献很多，但是大多是针对某种特定异常的离线检测方法[6,7]。因此，网络管理员亟需一种既能够在线地检测网络异常，又能够取得很好的检测性能的算法。

本文正是以此作为研究目标，提出一种基于奇异值分解更新的多元在线异常检测算法(MOADASVDU)。主要创新点包括以下两个方面：(1)利用奇异值分解的更新算法，提出了一种全网络异常的在线检测算法MOADA-SVDU，并对该算法的复杂度进行了分析；(2)通过分析因特网实测的流量矩阵数据集及模拟试验，证实了MOADA-SVDU算法的有效性。

2 MOADA-SVDU算法

本节首先描述能够刻画网络流量完整视图的流量矩阵模型，然后利用奇异值分解更新的方法以增量的方式建立能够刻画网络流量变化规律的常态模型，由此提出一种增量的多元在线异常检测算法MOADA-SVDU，最后对该算法的存储开销和时间复杂度进行理论分析。

2.1 流量矩阵模型

定义1 流量矩阵 假设某自治系统(Autonomous System, AS)有n个边界路由器，以一定的时间间隔(周期)连续地被动测量任意一对边界路由器之间的流量，然后将这些测量值排列成一个p×T的矩阵X，它表示所有这些流量测量值的时间序列。其中，T表示测量的周期数，p表示每个周期内测量获得的流量测量值的个数，即p=n×n；第i列表示在第i个周期内流量测量值向量，通常用Xi表示，第j行表示第j个路由器对之间流量测量值的时间序列。矩阵X称为AS的路由级流量矩阵，简称为流量矩阵。根据选择的流量测度，可以定义基于不同测度的流量矩阵：分组数矩阵、流数矩阵、字节数矩阵等。

2.2 MOADA-SVDU算法

流量异常检测的前提是建立网络流量的常态模型，然后根据这个常态模型来分析获得的测量样本，从而确定它们是正常的还是异常的。在离线异常检测中，通常以批处理的方式建立常态模型，从而确定在这批测量样本中哪些属于异常；而在在线异常检测中，通常要以增量的方式建立常态模型，每步只处理单个测量样本，判断该测量样本是否属于异常，并利用该测量样本更新常态模型。

许多规模较大的AS(如Abilene)通常具有十几个边界路由器。如果将AS所有边界路由器间的流量测量值看作一个输入向量Xi，则该向量Xi是存在于高维空间pℝ中的一个多元变量，流量矩阵X可以看作高维空间pℝ中多元变量的时间序列其中T表示测量的周期数。而PCA是处理类似流量矩阵高维数据的一种最有效的方法，它能够通过降低维度的方法实现最小均方意义下原始数据的重构。

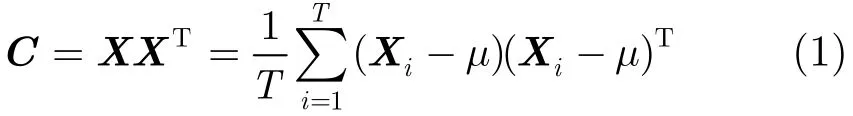
奇异值分解(Singular Value Decomposition,SVD)是实现PCA的另一种重要方法。直接对归一化的输入向量进行SVD如下：

因此

由式(1)-式(4)可以看出：对X的协方差矩阵C进行谱分解得到的特征向量矩阵与直接对X进行SVD得到的特征向量矩阵完全相等；而对X的协方差矩阵C进行谱分解得到的特征值矩阵是直接对X进行SVD得到的奇异值矩阵Σ的平方，即=2ΛΣ。因此，可以直接对X进行SVD，求取协方差矩阵C对应的特征值矩阵和特征向量矩阵，从而实现PCA。

但是，SVD同样属于批处理算法，它要求流量矩阵X必须提前给定。为了以增量的方式计算特征值矩阵和特征向量矩阵，本文引入一种SVD更新算法[8]。

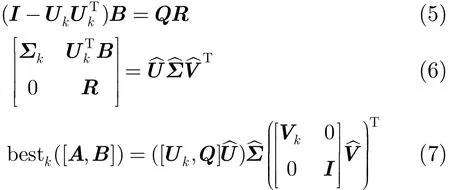
其中式(5)是对矩阵(I−Uk)B执行QR分解；式(6)是对矩阵[Σk,B;0,R]执行SVD；式(7)是根据式(5)，式(6)计算得到的有关参数计算矩阵[Ap×n,Bp×r]的秩-k近似矩阵。

本文在4.1节将通过实测数据分析表明MOADA-SVDU算法得到的残余向量与PCA算法得到的残余向量基本相同，而且对于同样的流量测度，相邻时期的流量矩阵对应的Q统计量阈值非常接近。因此，可以将前一阶段的流量矩阵作为训练集，并在该训练集上执行PCA算法以获得Q统计量阈值，然后以此作为下一阶段MOADA-SVDU算法的异常检测阈值。

基于以上基本原理，本文提出一种基于奇异值分解更新的多元在线异常检测算法MOADASVDU，算法流程见表1。

表1 MOADA-SVDU算法

对于在线异常检测算法来说，存储开销和时间复杂度是至关重要的两个指标。MOADA-SVDU算法可以分为两个阶段：在初始化阶段，需要存储X1；在增量检测阶段，需要存储Uk、Σk、Vk以及x。因此，MOADA-SVDU算法总的存储开销为p×n+p×k+k×k+n×k+p×1，而PCA算法的存储开销为p×T的流量矩阵。由于n≪T, k≪p，所以MOADA-SVDU算法的存储开销远小于PCA。

MOADA-SVDU算法在增量检测阶段的计算瓶颈是式(5)的QR分解和式(6)的SVD，其时间复杂度分别为Ο(p)和Ο(p×k)；而PCA算法的计算瓶颈是对整个流量矩阵执行谱分解，其时间复杂度为Ο(T×p2)。显然，MOADA-SVDU算法的时间复杂度远低于PCA。

3 算法评价

为评价MOADA-SVDU算法的检测性能，本文采用了两种方法：对因特网实测数据的分析以及对模拟试验数据的分析，并在同等条件下与PCA算法进行比较。

3.1 因特网实测数据的分析

(1)数据集 利用从Abilene实测得到的流量矩阵数据集[1,2,9]来评价MOADA-SVDU算法的检测性能，数据集的具体描述见表2。

(2)检测结果 选择表2中4种不同流量测度的数据集：Dataset1，Dataset2，Dataset4和Dataset5，分别画出输入向量2-范数的平方、PCA算法计算获得的残余向量2-范数的平方以及MOADA-SVDU算法计算获得的残余向量2-范数的平方，如图1(a)-1(d)所示。可以看出，MOADA-SVDU算法不仅实现了网络流量异常的在线检测，而且在大部分情况下都具有与PCA算法类似的检测性能。

异常检测阈值是影响MOADA-SVDU算法检测性能的重要参数，为了验证以Q统计量作为阈值的可行性，计算并画出表2中数据集Dataset1～Dataset6对应的Q统计量，其中Dataset1～Dataset3对应的Q统计量如图2(a)所示，Dataset4～Dataset6对应的Q统计量如图2(b)所示。可以看出，虽然不同测度的流量矩阵对应的Q统计量差异很大，但相邻时期的流量矩阵对应的Q统计量非常接近，这验证了3.2节中阈值选取方法的可行性。

表2 Abilene流量矩阵

图1 PCA和MOADA-SVDU算法对实测数据的检测结果

图2 不同的流量矩阵对应的Q统计量

3.2 模拟试验数据的分析

(1)模拟方法 考虑到网络流量通常由3种成分的流量构成[10]：近似周期性的正常成分、高斯噪声成分和异常成分。因此，我们产生这3种成分来并按照适当比例人工合成流量矩阵中每条OD流。具体步骤如下：

第1步 利用3种不同周期的正弦波叠加来模拟正常的OD流，并构造基准流量矩阵。

第2步 在第1步产生的基准流量矩阵的每条OD流上加入零均值的高斯噪声，获得不含异常的基准流量矩阵。

第3步 在第2步产生的含噪音的基准流量矩阵中以一定的规则加入各种典型异常，异常的合成步骤如图3所示。

由于本文重点关注流量大小异常的检测，所以本文模拟4种最常见的流量异常：阿尔法(alpha)异常、(分布式)拒绝服务攻击(DoS, DDoS)、闪拥(flash crowd)、入口/出口移动(ingress/egress shift)异常。这4种异常的具体特征见表3。

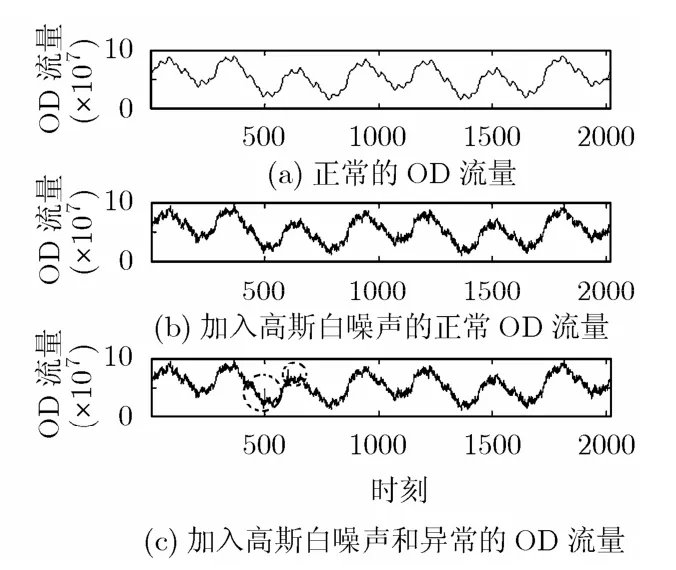
图3 异常的合成步骤

表3 异常类型及其特征

可以用4个参数来描述这4种网络流量异常[11]：持续时间、流量变化大小、源-目的数以及形状函数。当网络异常出现时，可以用两种方式模拟流量大小的变化：一是通过为基准流量矩阵中部分OD流乘上一个乘法因子，二是通过为基准流量矩阵中部分OD流加上一个常数项。源-目的数是指异常所涉及的OD流的数目，记号(1,1)表示异常涉及单个源和单个目的地，这可能是由于拒绝服务攻击或阿尔法事件，(N,1)表示异常涉及N个源点和1个目的地，这可能是由于出现了分布式拒绝服务攻击或闪拥，(2,2)表示异常涉及2个源点和2个目的地，这可能是由于入口/出口移动事件引起的。形状函数是用来模拟各种异常的变化行为，这些行为可以用不同的形状函数及其组合来表征。以上4个参数的可能取值见表4。

(2)检测结果 采用上述方法模拟4种不同的网络异常，来评价算法的检测性能。当模拟阿尔法事件或拒绝服务攻击时，从第1000时刻开始产生异常，持续时间为4个周期，将某条OD流的流量大小从增加20%迅速增加至80%。当模拟分布式拒绝服务攻击或闪拥事件时，从第1500时刻开始产生异常，持续时间为6个周期，将5条OD流的流量大小从增加10%迅速增加至50%，然后又逐渐降低至10%。当模拟入口/出口移动事件时，从第1700时刻开始产生异常，持续时间为40个周期，将某条OD流的流量大小减少50%，即为某条OD流的流量大小乘以0.5，且将减少的这部分流量加到另一条OD流上。检测结果如图4(a)所示，MOADA-SVDU算法能够非常准确地检测出这3种人造异常，与PCA算法的检测结果几乎完全相同。KRLS算法[9]的检测结果如图4(b)所示，显然无法通过设置某一阈值来检测异常，其中δt表示投影误差。因此，MOADA-SVDU算法的检测性能明显优于KRLS算法。

表4 异常参数及其取值

下面进一步研究MOADA-SVDU算法的敏感性。从第1000时刻开始产生异常，持续时间为10个周期，将某条OD流的流量大小从5%逐渐增加至50%，检测结果如图5(a)所示，在前4个周期，由于异常流量较小，所以无法被检测到，而从第1004-1009时刻成功检测到异常，由此可见，异常流量越大，MOADA-SVDU算法的检测性能越好。在第1500时刻，将某条OD流的流量大小增加20%，持续时间为5个周期，在第1550时刻，将某10条OD流的流量大小同时增加20%，持续时间也为5个周期，检测结果如图5(b)所示，异常分布范围越广，算法的检测性能越好，由此可见MOADA-SVDU算法尤其适合检测那些局部影响不大但影响范围较广的异常，如DDoS攻击。

4 结束语

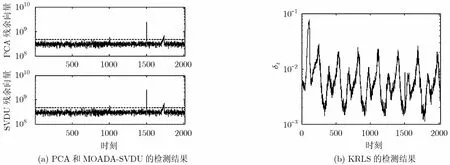
图4 PCA, MOADA-SVDU和KRLS算法对模拟试验数据的检测结果

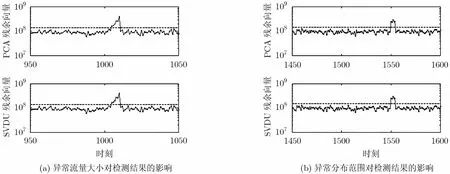
图5 MOADA-SVDU算法的敏感性分析

本文提出了一种基于奇异值分解更新的多元在线异常检测算法MOADA-SVDU，Abilene实测的流量矩阵数据和模拟试验数据分析表明该算法不仅实现了网络流量的在线检测，而且取得了与批处理算法PCA类似的检测性能，完全能够满足网络管理员在线有效地检测网络异常的需要。近期的研究表明PCA异常检测器自身也会遭受方差注入攻击[12]，且流量矩阵可能出现丢失元素值的情况[13]，因此下一步我们将研究更为鲁棒的PCA异常检测方法。

[1] Lakhina A, Crovella M, and Diot C. Diagnosing network-wide traffic anomalies[C]. SIGCOMM, Portland,Oregon, USA, 2004: 224-235.

[2] Lakhina A, Crovella M, and Diot C. Mining anomalies using traffic feature distributions[C]. SIGCOMM, Philadelphia,Pennsylvania, USA, 2005: 164-175.

[3] Jin Y, Sharafuddin E, and Zhang Z L. Unveiling core network-wide communication patterns through application traffic activity graph decomposition[C]. SIGMETRICS,Seattle, WA, USA, 2009: 86-91.

[4] Torres R, Hajjat M, and Rao S G, et al.. Inferring undesirable behavior from P2P traffic analysis[C]. SIGMETRICS, Seattle,WA, USA, 2009: 156-167.

[5] Logg C, Cottrell L, and Navratil J. Experiences in traceroute and available bandwidth change analysis[C]. SIGCOMM Workshop, Portland, Oregon, USA, 2004: 81-90.

[6] 吴志军, 张东. 低速率DDoS攻击的仿真和特征提取[J]. 通信学报, 2008, 29(1): 71-76.Wu Z J and Zhang D. Attack simulation and signature extraction of low-rate DDoS[J]. Journal on Communications,2008, 29(1): 71-76.

[7] 谢逸, 余顺争. 基于Web用户浏览行为的统计异常检测[J].软件学报, 2007, 18(4): 967-977.Xie Y and Yu S Z. Anomaly detection based on web users’browsing behaviors[J]. Journal of Software, 2007, 18(4):967-977.

[8] Zhao H, Yuen P C, and Kwok J T. A novel incremental principal component analysis and its application for face recognition[J]. IEEE Transactions on Systems, Man, and Cybernetics-Part B: Cybernetics, 2006, 36(3): 873-886.

[9] Ahmed T, Coates M, and Lakhina A. Multivariate online anomaly detection using kernel recursive least squares[C].INFOCOM, Los Angeles, USA, 2007: 387-396.

[10] Lakhina A, Papagiannaki K, and Crovella M, et al..Structural analysis of network traffic flows[C]. SIGMETRICS,New York, NY, USA, 2004: 156-167.

[11] Soule A, Salamatian K, and Taft N. Combining filtering and statistical methods for anomaly detection[C]. IMC, Boston,USA, 2005: 168-179.

[12] Rubinstein B, Nelson B, and Huang L. Stealthy poisoning attacks on PCA-based anomaly detectors[C]. SIGMETRICS,Seattle, WA, USA, 2009: 168-179.

[13] Zhang Y, Roughan M, and Willinger W, et al..Spatio-temporal compressive sensing and Internet traffic matrices[C]. SIGCOMM, Barcelona, Spain, 2009: 110-121.