含旋转部件目标双基地ISAR微动特征提取及成像研究

朱仁飞 张 群② 罗 迎 朱小鹏

①(空军工程大学电讯工程学院 西安 710077)②(复旦大学波散射与遥感信息国家教育部重点实验室 上海 200433)

1 引言

双基地逆合成孔径雷达(Bi-ISAR)因其具有良好的 “四抗性能”，以及对目标成像时不受目标运动方向限制等特点使之成为雷达成像领域的一个重要研究方向[1−4]。而微多普勒效应(micro-Doppler effect)是指目标或目标结构中的微动部件使目标回波信号的多普勒频率发生展宽，并会使目标像产生模糊现象[5−8]。实现目标微动信息的有效分离与提取，除了可以得到清晰目标主体像外，还能获得目标的精细运动特征，并且进一步确定目标微动部件与目标主体之间的位置关系，从而为目标的识别与分类提供更为丰富的信息。

近年来，许多有效的微多普勒信息分离与提取技术相继被提出，如时频分析技术[9]、匹配追踪法[10]、经验模式分解(EMD)[11]、扩展Hough变换法[12]等。但这些方法都是针对单基雷达的，其在收、发分置的双基地雷达系统中是否适用则还尚未研究。本文以自然界中最为常见的微动形式——旋转运动为例，首先建立了含旋转部件运动目标的双基地ISAR系统数学模型，并详细分析了目标结构部件旋转所产生的微多普勒效应。在分析研究了目标微多普勒在距离-慢时间谱图域的表现形式及其特点后，针对双基地雷达收、发分置的特殊空间构成，修正了基于扩展Hough变换的谱图域提取目标微动信息的方法，最终获得双基体制下雷达目标的真实微动信息和清晰主体像。

2 双基地雷达系统微多普勒信息分析

2.1 双基地雷达微多普勒数学原理

在图1所示的双基地ISAR平面内，含旋转部件的雷达目标以速度V沿水平方向运动。雷达坐标系(X, Y)以发射雷达TX为原点，基线为X轴，假设双基地雷达的基线长度为L，则接收雷达RX的坐标为(L,0)。在目标模型中包含两类典型的散射点，即(1)与双基地雷达之间只存在平动关系的目标主体散射点，它包括目标中心O(xO,yO)、旋转中心Q(xQ,yQ)和其它非旋转点；(2)旋转点P，其旋转半径、频率以及初相分别为r, ω, θ。

图1 运动目标双基地雷达系统

由于目标主体散射点只存在平动，所以在慢时间tm时刻，主体散射点i到发射雷达和接收雷达的距离RTi(tm),RRi(tm)可分别表示为

则tm时刻点i的双基地雷达距离和为

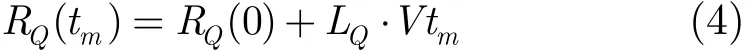
在双基地雷达系统中，目标尺寸远小于目标中心到收、发雷达之间的距离，而且旋转点的距离变化量(旋转半径)是微小的变化量。因此，旋转点P到收、发雷达之间的距离RRP(tm),RTP(tm)可以分别近似为其在RXQ(tm),TXQ(tm)上的投影RTM(tm)和RTN(tm)，其中RXQ(tm),TXQ(tm)分别表示为tm时刻旋转中心Q与收、发雷达之间的连线。

如图2所示，旋转点P以Q中心作周期性的旋转，并假设在tm时刻，旋转点P到旋转中心Q的距离矢量为rP(tm)，则其在目标本地坐标系(x, y)中的坐标为

通过投影近似，点P到发射、接收雷达距离可写为

图2 旋转点距离计算示意图

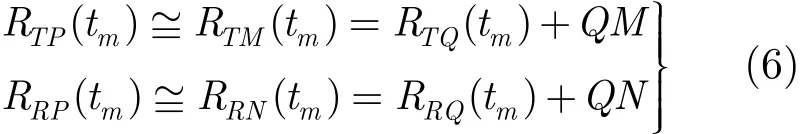
其中QM , QN分别为矢量rP(tm)在TXQ(tm),RXQ(tm)上的投影距离，且有

由于目标尺寸较小，所以目标上任意散射点的发射、接收角都可以用目标中心O的发射、接收角(∠OTXRX,∠ORXTX)来近似。在双基地ISAR成像累积时间内(一般大约为3～5 s)，目标的运动会导致角(∠OTXRX,∠ORXTX)发生变化(一般在数度左右)，但相对目标部件旋转所引起∠PQM,∠PQN 的变化，其时变性基本可以忽略。因此，可以将角(∠OTXRX,∠ORXTX)视为常数，并令其分别等于αT,αR。则式(7)可近似写为

将式(8)代入式(6)，并整理后可得到旋转点P的双基地距离和为

将旋转中心Q的双基地雷达距离和RQ(tm)代入式(9)，则有

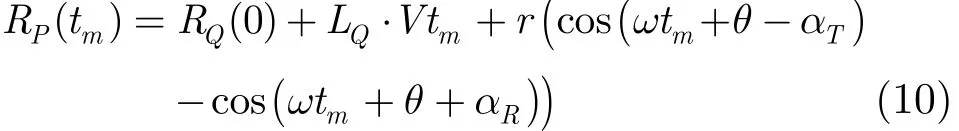
2.2 含旋转部件目标的双基地ISAR回波信号分析

假设双基地ISAR系统发射线性调频信号，则目标上任一散射点i的回波信号可写为

其中fc, Tp, μ分别为雷达信号的中心频率、脉冲宽度和调频率，rect(˙)为矩形窗函数。若以目标中心O为参考点，则由式(3)可得tm时刻参考点的瞬时距离Rref(tm)为

将式(12)代入式(11)可得参考点的回波信号为

其中Tref为参考信号的脉冲持续时间，一般地，它略大于雷达信号脉冲宽度Tp，对目标回波信号进行拉伸处理后，可得

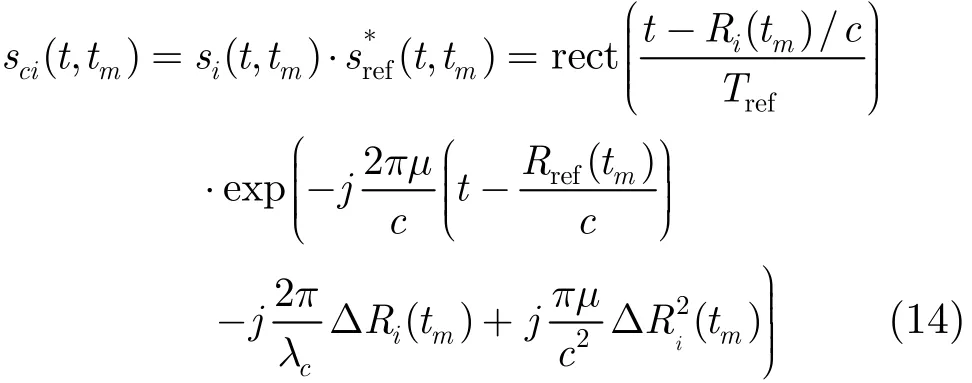
其中ΔRi(tm)表示在tm时刻，目标散射点和参考点的双基地雷达距离和之间的差值。

其中式(14)中的相位项分为3部分，第1项为距离项，该项变换后可获得目标散射点的距离分布信息；第2项是多普勒项，它包含目标运动产生的多普勒频率信息；第3项为剩余视频相位，它会使多普勒有轻微改变[13]。对式(14)中相位项的第2项分别求关于慢时间tm的导数，可得旋转中心Q和旋转点P产生的多普勒频移分别为

从式(16)中可以看出：旋转中心点产生Q的多普勒频率是与慢时间tm无关的常数，它只与目标的平动有关，该结论对目标所有主体散射点成立；旋转散射点产生的多普勒频率由随目标主体平动产生的多普勒频率和自身旋转所产生的微多普勒频率项构成。

对目标回波信号Sci(t, tm)求关于快时间t的傅里叶变换可得

从式(17)可以看出，经过快时间变换后的回波信号在任一tm时刻都是一系列波形为sinc函数的尖脉冲。尖脉冲在频率轴上的峰值出现的频率为fi=−ΔRi(tm)⋅μ/c ，它与ΔRi(tm)成一一对应的关系，通过对其乘以因子−c/μ，就可以分别得到目标散射点与参考点双基地雷达距离和之间差值ΔRi(tm)，也就可以得到各散射点的分布信息。则旋转中心Q和旋转点P在频率轴上的峰值位置所对应的频率为

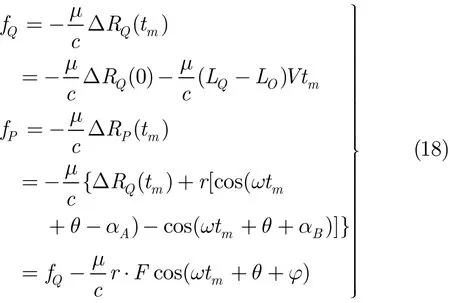
为附加相位项。在式(18)中，(LQ−LO)⋅Vtm与ΔRQ(tm)相比，其值基本可以忽略。例如，在仿真实验的第3种参数配置下，当ΔRQ(tm)=4.22 m 时，由(LQ−LO)⋅Vtm在两次回波信号中产生的距离差仅仅为0.03 mm，所以忽略这一项是可行的。因此可以有ΔRQ(tm)≅ΔRQ(0)，将其代入式(18)后，可得

从式(19)可以看出：旋转中心点在频率轴上出现的位置是固定的，它与慢时间tm无关，其它目标主体散射点也同样如此；旋转散射点在频率轴上的位置会随慢时间作周期性变化。因此，作为频率(或距离)-慢时间的2维函数，含旋转部件目标的双基地ISAR回波谱图，将由目标主体散射点产生的直线谱和旋转点产生的正弦曲线谱组成，且旋转点对回波信号调制产生的正弦曲线谱变化周期与其旋转周期相同。式(19)同时说明，旋转点在谱图上产生的正弦曲线还受到了目标与空间几何位置的调制，具体表现在双基地空间关系影响因子和附加相位项的影响，这一点与单基雷达体制下的微多普勒效应有本质区别。

3 改进的扩展Hough变换算法

扩展Hough是谱图域微多普勒信息提取的较为有效的方法之一[12]。根据扩展Hough变换理论，可以使用4参数公式将谱图上的正弦曲线描述为

其中d为最大幅度，w是角频率，w=2π/Tr，Tr是正弦曲线的周期，ϕ0代表初始相位，l描述了正弦曲线在频率(距离)轴的位置。通过从谱图域中提取的曲线参数信息，经过换算就可以得到目标的微动信息，并进一步实现目标微动信息的分离。

在双基地ISAR系统中，由于双基地空间位置对目标曲线谱产生的影响。使得利用扩展Hough变换无法直接获得目标的真实旋转半径和相位信息。由于旋转相位包含了旋转部件出现的位置信息，不能精确估计旋转部件位置也就无法对目标特殊部件(如舰艇上旋转的雷达天线等)进行的有效干扰或精确打击；而不真实的旋转半径信息也会造成对目标的误判。因此，为了得到真实的旋转信息必须消除双基地空间因子F和附加相位项ϕ的影响，也就必须对扩展Hough方法进行修正和改进。图3给出了在双基地ISAR系统中，利用修正的扩展Hough方法提取和分离目标微动信息的流程示意图，其中虚线方框内表示修正步骤。

图3 双基地ISAR微动信息分离与提取流程示意图

4 仿真分析

图4 双基地雷达系统模型图

如图4所示，设定4组双基地雷达配置参数对比分析双基地ISAR系统中微多普勒的特点，对应的基线长度为别为(0,5,10,15) km。当基线长度为0 km时，收、发雷达处于同一位置，系统退化为单基体制雷达。假设雷达发射带宽为B=300 MHz 线性调频信号，其脉冲重复频率PRF=1000 Hz ，载频fc=10 GHz ，对应的波长λc=0.03 m 。假设目标以速度V=300 m/s沿基线平行方向运动，目标中心与发射雷达初始距离为10 km。

假设目标由 5个非旋转点和2个旋转点组成，如图5所示。其中：两个旋转点在目标坐标系中的初始坐标分别为(3 m,3 m)和(0 m,3 m)，且各自以半径(4 m,8 m)和频率(4 Hz,12 Hz)绕旋转中心旋转，其起始相位均为0。则图6给出了4种参数下的双基地ISAR信号距离-慢时间2维谱图，从图中可以看出：(1)含旋转部件目标的双基地ISAR 2维谱图由非旋转点产生的直线谱和旋转点产生的正弦曲线谱构成；(2)目标结构部件旋转所产生的正弦曲线谱的幅度受到目标的双基地空间位置的调制，使其具有鲜明的双基地特征。

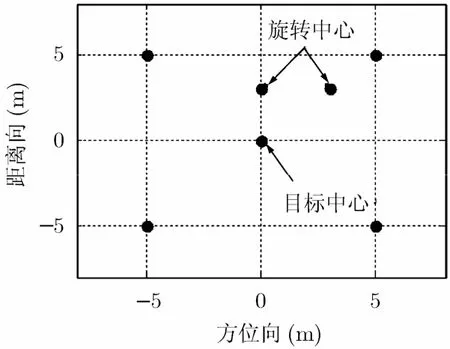
图5 目标散射点模型

表1给出了4种雷达系统配置参数下基线长度、双基地空间因子、附加相位以及利用扩展Hough方法和修正的扩展Hough方法所提取的目标旋转部件信息(半径和起始相位)。从表1可以看出：利用扩展Hough变换提取曲线谱参数所直接得到目标旋转点半径与其真实半径差异较大；而经过双基地空间因子换算步骤处理，即利用修正的扩展Hough变换所得到的旋转半径与目标旋转点真实半径基本一致。另外，通过表1中所给出的附加相位项，还能得到目标旋转部件真实位置信息。

图7给出了第3种参数配置下，微多普勒信息分离前后含旋转部件的双基地ISAR目标像。从图7可以看出：未分离微多普勒信息的目标双基地ISAR像出现模糊现象，在分离目标旋转部件产生的微多普勒信息后，将得到清晰的目标主体像。

5 结论

本文以含旋转部件目标为例，分析研究了双基地ISAR系统中目标结构部件微动所产生微多普勒信息的特点及其提取方法。研究结果表明：在双基地ISAR系统中，旋转形式的微动所产生的微多普勒频率服从正弦规律调制，但微多普勒频率变化振幅受目标与双基地雷达空间位置即双基地空间因子调制，使其具有鲜明的双基地特性。利用修正后的扩展Hough变换技术可以从双基地ISAR谱图中有效地提取目标的真实微动信息，并进一步得到分离目标微动信息后的清晰主体像，从而为基于双基地雷达目标的识别提供新的途径和方法。

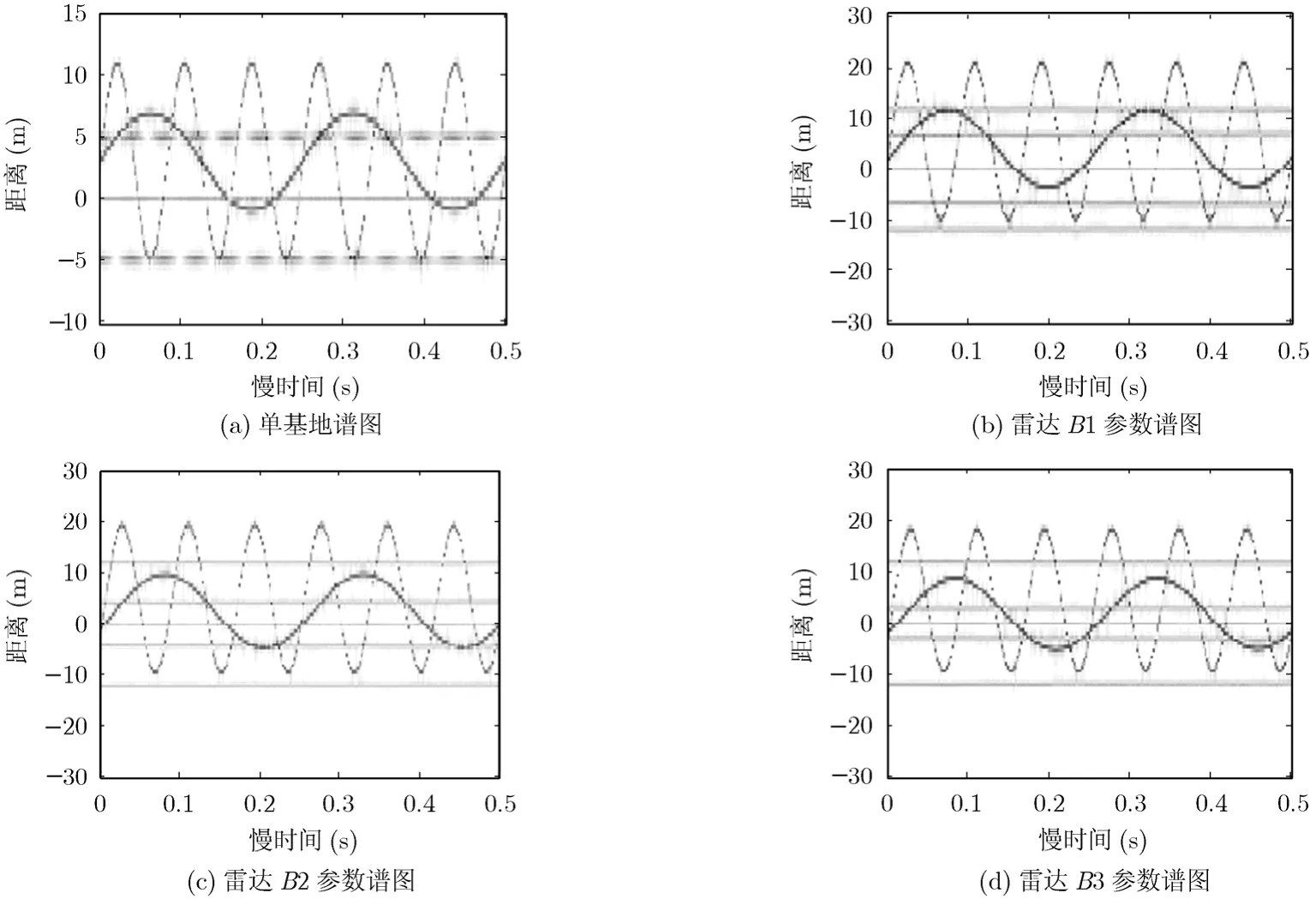
图6 含旋转部件目标双基地ISAR距离-慢时间谱图

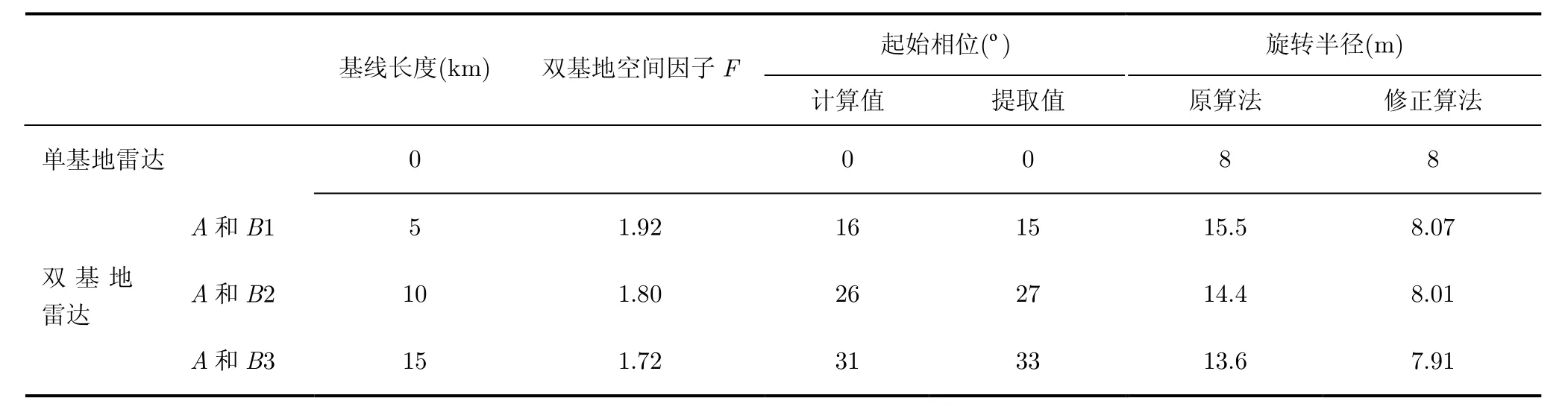
表1 4种雷达系统微动特征表

图7 微多普勒信息分离前后的含旋转部件目标双基地ISAR像

[1] Martorella M, Palmer J, and Litteton B. On bistatic inverse synthetic aperture radar [J]. IEEE Transactions on Aerospace and Electronic Systems, 2007, 43(3): 1125-1143.

[2] 高昭昭, 梁毅, 邢孟道等. 双基地逆合成孔径雷达成像分析[J].系统工程与电子技术, 2009, 31(5): 1055-1059.Gao Zhao-zhao, Liang Yi, and Xing Meng-dao, et al.. Analysis of ISAR imagery for bistatic radar [J]. Systems Engineering and Electronics, 2009, 31(5): 1055-1059.

[3] 张亚标, 朱振波, 汤子跃, 等. 双站逆合成孔径雷达成像理论研究[J]. 电子与信息学报, 2006, 28(6): 969-972.Zhang Ya-biao, Zhu Zhen-bo, and Tang Zi-yue, et al.. Bistatic inverse synthetic aperture radar image formation [J]. Journal of Electronics and Information Technology, 2006, 28(6):969-972.

[4] 黄艺毅, 王军锋, 刘兴钊. 双站ISAR成像算法的研究[J]. 信号处理, 2007, 23(4A): 514-517.Huang Yi-yi, Wang Jun-feng, Liu Xing-zhao. Research on bistatic ISAR imaging algorithm [J]. Signal Processing, 2007,23(4A): 514-517.

[5] Chen V C, Li F Y, and Ho S-S, et al.. Micro-Doppler effect in radar: phenomenon, model and simulation study [J]. IEEE Transactions on Aerospace and Electronic Systems, 2006,42(1): 2-21.

[6] Thayparan T, Lampropoulos G, and Wong S K. Distortion in the inverse synthetic aperture radar images of a target with time-varying perturbed motion [J]. IEEE Proceedings on Radar, Sonar and Navigation, 2003, 150(4): 221-227.

[7] 陈行勇, 刘永祥, 姜卫东, 等. 微动目标合成距离像数学分析[J], 电子学报, 2007, 35(3): 585-589.Chen Hang-yong, Liu Yong-xiang, and Jiang Wei-dong, et al..Mathematics of synthesizing range profile of target with micro-motion [J]. Acta Electronica Sinica, 2007, 35(3):585-589.

[8] 庄钊文, 刘永祥, 黎湘. 目标微动特性研究进展[J]. 电子学报,2007, 35(3): 520-525.Zhuang Zhao-wen, Liu Yong-xiang, and Li Xiang. The achievements of target characteristic with micro-motion [J].Acta Electronica Sinica, 2007, 35(3): 520-525.

[9] Chen V C, Li F, and Ho S S, et al.. Analysis of micro-Doppler signatures. IEE Proceedings -Radar Sonar Navigation, 2003,150(4): 271-276.

[10] Mallat S and Zhang Z. Matching pursuit with time-frequency dictionaries [J]. IEEE Transactions on Signal Processing,1993, 41(12): 3397-3415.

[11] Bai Xue-ru, Xing Meng-dao, and Zhou Feng, et al.. Imaging of micromotion targets with rotating parts based on empirical-mode decomposition [J]. IEEE Transactions on Geoscience and Remote Sensing, 2008, 46(11): 3514-3523.

[12] Zhang Qun, Yeo Tat-soon, and Tan Hwee-siang, et al..Imaging of a moving target with rotating parts based on the Hough transform [J]. IEEE Transactions on Geoscience and Remote Sensing, 2008, 46(1): 291-299.

[13] 保铮, 邢孟道, 王彤. 雷达成像技术[M]. 北京: 电子工业出版社, 2005: 26-28.