基于窄带测距信息的空间目标微动特征检测与估计

马 梁 王雪松 李永祯 刘 进

(国防科学技术大学电子科学与工程学院 长沙 410073)

1 引言

弹道中段时间长、目标运动简单，被认为是弹道导弹识别、拦截的关键阶段。在中段，由于不受空气阻力的影响和弹箭分离与诱饵释放时不可避免的横向干扰，弹头和诱饵在飞行过程中存在不同形式的微动[1]。弹头的进动频率一般为亚赫兹的量级，而对于诱饵和其它碎片，一般没有采取姿态控制方式，目标会呈现翻滚等随机的运动方式。其翻滚频率可达十几甚至几十赫兹[2]。弹头和诱饵在微运动特性上的差异为空间非合作目标探测与识别提供了一条可行的途径，也成为了弹道中段目标识别研究的热点领域之一。

文献[3,4]比较全面地分析了刚体和非刚体目标的微运动特点和微运动特征提取方法，为空间目标的微运动分析与识别建立了数学基础；在国内，国防科技大学、中国航天科工集团、西安电子科技大学等多家研究小组围绕空间目标微动特征提取开展了深入的工作，主要包括基于目标回波的微多普勒分析[5,6]和基于目标雷达特性(RCS，一维距离像等)的二次特征提取[7,8]等，但需要指出的是，微运动和微多普勒的概念最初来源于相干激光雷达，地基防御雷达在什么条件下可以检测出来袭目标的微运动信息目前在国内外尚无共识，关于这方面的分析还未见到公开报道。

线性调频信号由于具有脉冲压缩和使用简便等优点而被广泛运用于雷达和声纳，这种信号的一个显著特点就是具有很强的距离-多普勒耦合效应。在导弹攻防对抗条件下，为了实现3000～4000 km的作用距离，发射脉冲宽度增加到了毫秒量级，引起距离-多普勒耦合系数成数量级增大[9]。当这种形式的线性调频信号对微动目标进行照射时，由于微多普勒的存在，将会使雷达的测量距离发生偏差，这种偏差的大小甚至和雷达的距离分辨力相当，可以被窄带跟踪雷达所观测到，从而可以作为空间目标微动特征检测和参数估计的依据。

经分析可知，振动、旋转、锥旋等微运动造成的目标径向距离变化都可统一为余弦形式，在较短的观测时间内，可近似用匀速转动模型表征。本文首先比较了目标做匀加速直线运动和匀加速叠加匀速转动这两种不同运动时，雷达测量距离随时间变化规律的差异，指出匀速转动引起的测距偏差可达若干个距离分辨单元。在此基础上，提出了基于窄带测距信息的空间目标微动特征检测流程和参数估计新方法，依据典型参数，对检测概率和参数估计性能进行了仿真分析。最后，利用微动目标暗室动态测量实验的数据进一步验证了本文的观点和参数估计算法。

2 信号模型

当雷达发射线性调频信号时，由于存在距离-多普勒耦合效应，雷达对目标的测量距离Rmeas可以表示为[9]

其中Rn为第n个脉冲起始时刻时目标的真实距离，vn为第n个脉冲起始时刻时目标的径向速度，为由于噪声存在而引起的测量误差。Δt=f0τ/B 为距离-多普勒耦合系数，它是线性调频信号独有的特性，与目标运动状态无关。f0为雷达的载频，τ为脉冲宽度，B为线性调频脉冲的调制带宽。

根据雷达信号相关理论，在只考虑平稳高斯白噪声的影响时，距离测量误差可以认为服从零均值的高斯分布，其最小均方误差为[10]

其中c为真空中光速，S/N为信噪比。

2.1 目标做匀加速直线运动

当目标做匀加速直线运动时，目标距离Rn和速度vn可表示为

其中R1，v1为脉冲串中第1个脉冲起始时刻时目标的位置和速度，n为脉冲数，Tr为脉冲重复周期。

将式(3)代入式(1)可得目标做匀加速直线运动时，距离测量值随脉冲数n(时间)的变化规律为

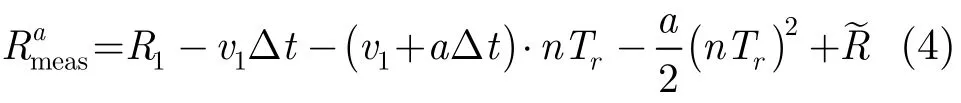
由式(4)可见，目标做匀加速运动时，其距离测量值随时间呈二次函数规律变化，当加速度不大时，近似为线性变化。图1(a)中的虚线给出了目标运动速度1000 m/s，加速度10 m/s2时，距离测量值随时间变化的曲线。

2.2 目标做匀加速直线叠加匀速转动

当目标相对于雷达做匀加速直线运动的同时叠加了匀速转动，目标距离Rn和速度vn可表示为

其中Rω为转动半径，ω为转动速度，φ1为脉冲串中第1个脉冲起始时刻时目标转过的角度。

同理，将式(5)代入式(1)可得目标做匀加速运动叠加匀速转动时，距离测量值随脉冲数n(时间)的变化规律为

由式(6)可见，当目标做匀速转动时，其距离测量值和仅有平动时相比，将产生正弦规律的偏差，偏差的大小由线性调频信号的参数和目标的运动参数共同决定。

图1 两种运动目标探测距离随时间变化曲线

图1(a)中的实线给出了目标质心运动速度1000 m/s，加速度10 m/s2，转动半径Rω=1m，转速ω=4πrad/s ，雷达载频f0=10 GHz ，脉宽τ=3 ms，带宽B=10 MHz 时，目标探测距离随时间变化的曲线。将上述参数代入式(6)中可计算出由转动引起的测距偏差可达±37.7 m，而此时的距离分辨单元为15 m，因此，这种转动引起的偏差可以被跟踪雷达所观测到，以作为目标微动特征检测的依据。图1(b)给出了两种不同运动形式的目标距离测量值之差随时间的变化关系曲线。

3 目标微动特征的检测与估计

对中段目标而言，不进行机动时，目标质心加速度为地球引力加速度g，在数秒内，目标相对于地心转过的角度极小，因此，可认为目标质心加速度的方向和大小都未发生变化，近似做匀加速直线运动。而振动、旋转、锥旋等微运动造成的目标径向距离变化则可统一为余弦形式，因此可近似用2.2节所提到的匀速转动模型描述。

3.1微动特征检测

通过第2节分析可以看出，当目标进行匀加速直线运动时，其跟踪距离随时间呈二次函数规律变化。而当目标在平动的基础上叠加匀速转动时，跟踪距离将出现正弦规律的偏差，因此，对目标微动特征的检测可按照以下步骤进行。

假设待处理时间T内雷达共发射了N个线性调频脉冲，则

步骤1 记录时间T内，目标的跟踪距离序列R(n)，0≤n≤N −1；

步骤2 对R(n)按照二次多项式的形式进行最小二乘拟合，得到系数a1、a2、a3；

步骤3 由系数a1、a2、a3获得(n)=a1(nTr)2+a2(nTr)+a3；

则目标微动特征的检测问题就转化为如下的二元假设检验问题：其中H0假设目标做匀加速直线运动，H1假设目标做匀加速直线运动叠加匀速转动；(n)服从零均值的高斯分布，其方差由式(2)表征，Aω=

根据估计和检测的相关理论[11]，幅度、频率、初相都未知的正弦信号的检验统计量可表示为

判H1成立。其中maxI(f)表示信号周期图的峰值。

记虚警概率为Pfa，则而检测概率可表示为[11]

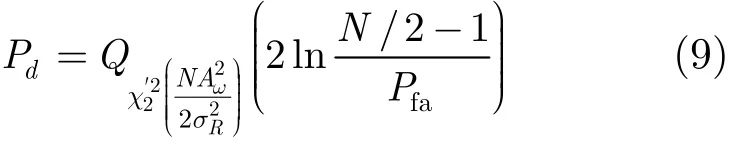
综上所述，基于窄带测距信息的目标微动特征检测的具体流程如图2所示，图中γ'为式(8)中不等式右端部分，即

由前面的分析可以看出，基于窄带测距信息的目标微动特征检测首先需要对目标建立稳定跟踪，因此，不妨令检测时的最小信噪比SNRmin=13 dB[9]，则由式(2)可得σR=1.31 m。若Pfa=10−12、N=480时，由式(9)可以算出，时，目标的微动特征检测概率大于90%，时，目标的微动特征检测概率趋近于1。对一般的空间目标而言，其旋转速度在亚赫兹到十几赫兹的量级，而旋转半径大都在0.5 m以上，若取目标旋转速度0.2 Hz，旋转半径0.5 m，雷达载频010 GHz f=，脉宽τ=1.5 ms，带宽10 MHz B=，此时检测概率趋近于1。可见，在导弹攻防对抗条件下，在对目标稳定跟踪后，按照本文提出的方法，可以实现极高概率的微动目标检测。

图2 基于窄带测距信息的目标微动特征检测流程

3.2 微动特征估计

在对微动目标正确检测的基础上，亦可完成对其旋转半径和旋转速度的参数估计，式(8)取最大值时的频率f0即为目标旋转速度的估计值，而Aω的估计值则可以表示为[11]

由式(10)，目标的旋转半径估计值可写为

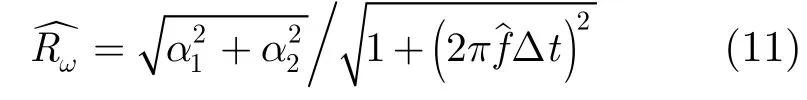
图3为旋转半径和旋转速度估计值随目标微动参数的变化规律的仿真结果。其中雷达载频f0=10 GHz，脉宽τ=1.5 ms ，带宽B=10 MHz ，脉冲重复周期PRI=8.5 ms ，虚警概率为10−12；目标距雷达的初始距离R1=500 km ，目标速度v0=4000 m/s，加速度a=10 m/s2，对4.08 s内的480个脉冲进行参数估计。

图3(a)给出了旋转速度为0.24 Hz时，转速估计的均值和标准差随旋转半径的变化规律。可以看出，目标旋转半径越大，对其转速的估计性能越高。图3 (b)给出了旋转半径为0.5 m时，旋转半径估计值的均值和标准差随旋转速度的变化规律，由图可见，随着旋转速度的增大，旋转半径的估计值并未收敛于其真值，而是发生了振荡性的变化，这是由于旋转速度的估计值只能是1/Ttotal的整数倍，目标的真实转速偏离1/Ttotal整数倍越多，的估计误差越大，从而旋转半径的估计误差也就越大。当对旋转速度遍历时，也就发生了如图3(b)中的振荡现象。

图3 参数估计统计量与目标微动参数的关系

4 暗室实测数据验证

在理论分析和仿真实验的基础上，设计了空间进动目标的暗室测量实验，实验场景如图4所示。目标体为作者所在的课题组自主设计开发的目标进动模拟实验平台。发射信号载频10 GHz，脉宽τ=1.5 ms ，带宽B=10 MHz ，脉冲重复周期PRI=14 ms ；目标距测量设备约15 m，进动轴与雷达视线的夹角为90°，参与检测和估计的脉冲数为500个，检测积累时间约7 s。

图5给出了表1中实验1条件下的实测数据处理结果，图5(a)为跟踪距离R(n)随时间变化的曲线，可以看出，当目标进动时，其探测距离变化约为±3 m，远远超出了目标真实位置的改变。由于目标未进行平动，因此可直接对R(n)做DFT以估计其进动频率，得到结果如图5(b)所示，表1则给出了不同实验条件下转动频率和转动半径的估计结果，可以看出，本文提出的参数估计方法能够较准确估计出目标的微动频率和转动半径。需要指出的是，由于暗室测量的噪声很小，表1中的估计结果都是在高信噪比条件下得到的，因此，在转动半径和转动速度都不大的情况下，同样可以实现参数估计。

图4 动态测量实验暗室环境

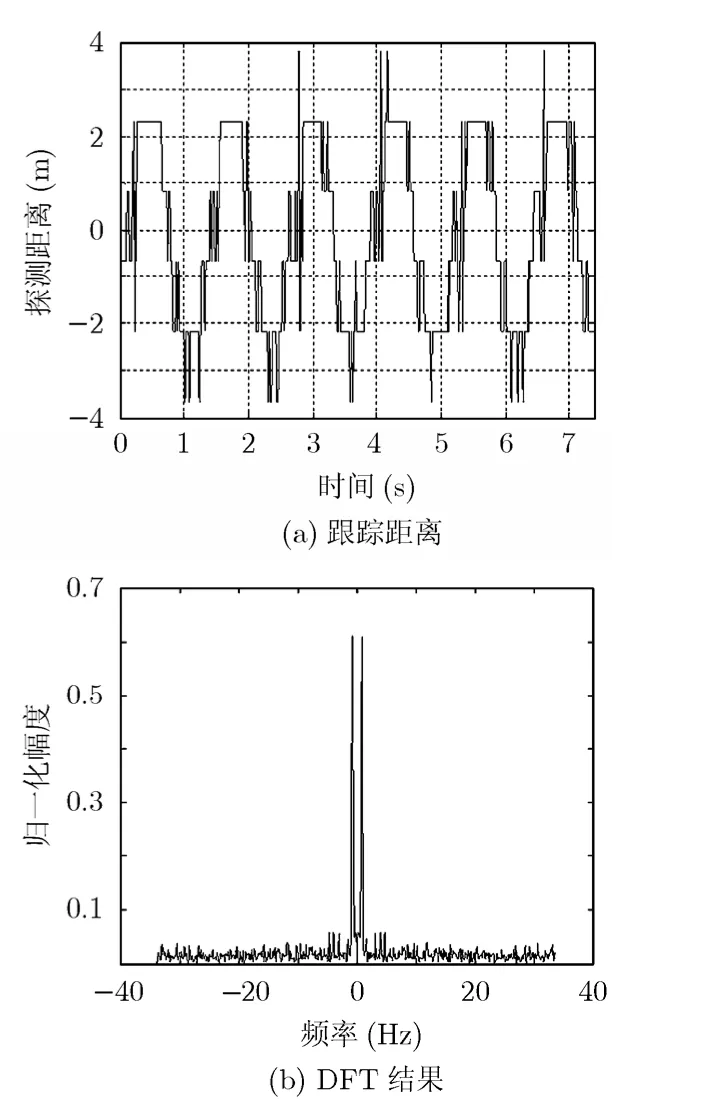
图5 实验1估计结果

表1 微动参数估计结果

5 结论

本文以空间微动目标检测为背景，研究了基于窄带跟踪距离的微动目标检测与微动参数估计新方法。首先比较了目标做匀加速直线运动和匀加速叠加匀速转动时，跟踪距离随时间的变化规律，指出当目标做匀速转动时，跟踪距离产生正弦规律的偏差，这种偏差的大小和窄带距离分辨单元相当，可以被雷达所观测到。在此基础上，提出了空间微动目标的检测流程和微动参数估计方法，根据空间目标精密跟踪雷达的典型参数设计了仿真实验，实验结果表明，在信噪比大于13 dB的情况下，典型微动目标的检测概率趋近于1。最后，利用微动目标暗室动态测量数据进一步验证了本文的观点和参数估计方法。本文的研究成果对于空间目标的检测、跟踪和识别，微多普勒分析与特征提取等方面具有借鉴意义。

[1] 庄钊文, 刘永祥, 黎湘. 目标微动特性研究进展[J]. 电子学报,2007, 35(3): 520-525.Zhuang Zhao-wen, Liu Yong-xiang, and Li Xiang. The achievements of target characteristic with micro-motion[J].Acta Electronica Sinica, 2007, 35(3): 520-525.

[2] 王涛. 弹道中段目标极化域特征提取与识别[D]. [博士论文],国防科技大学, 2006.Wang Tao. Feature extraction and recognition of targets in ballistic midcourse in polarization-domain [D]. [Ph.D.dissertation], National University of Defense Technology,2006.

[3] Chen V C, Li F, and Ho S S, et al.. Micro-Doppler effect in radar: phenomenon, model and simulation study[J]. IEEE Transactions on Aerospace and Electronic Systems, 2006,42(1): 2-21.

[4] Chen V C, Li F, Ho S S, and Wechsler H. Analysis of micro-Doppler signatures[J]. IEE Proceedings Radar Sonar Navigation, 2003, 150(4): 271-276.

[5] 刘进, 马梁, 王雪松, 王国玉. 微多普勒的参数化估计方法[J].信号处理, 2009, 25(11): 1759-1765.Liu Jin, Ma Liang, Wang Xue-song, and Wang Guo-yu.Extraction method of micro-Doppler based on TFD-Hough transform[J]. Signal Processing, 2009, 25(11): 1759-1765.

[6] Sun Hui-xia and Liu Zheng. Micro-Doppler feature extraction for ballistic missile warhead[C]. International Conference on Information and Automation Proceedings, Zhangjiajie,China, June 20-23, 2008: 1333-1336.

[7] 胡杰民, 付耀文, 黎湘. 空间锥体目标进动周期估计[J]. 电子与信息学报, 2008, 30(12): 2849-2853.Hu Jie-min, Fu Yao-wen, and Li Xiang. Precession cycle estimation of cone-shaped spatial target[J]. Journal of Electronics & Information Technology, 2008, 30(12):2849-2853.

[8] 贺思三, 周剑雄, 付强. 利用一维距离像序列估计弹道中段目标进动参数[J]. 信号处理, 2009, 25(6): 925-929.He Si-san, Zhou Jian-xiong, and Fu Qiang. Using HRRR sequence to estimate the precession parameters of midcourse target[J]. Signal Processing, 2009, 25(6): 925-929.

[9] 赵峰. 弹道导弹防御跟踪制导雷达跟踪技术研究[D]. [博士论文], 国防科技大学, 2007.Zhao Feng. Study on detection techniques of tracking and guiding radars in ballistic missile defense [D]. [Ph.D.dissertation], National University of Defense Technology,2007.

[10] 林茂庸, 柯有安. 雷达信号理论[M]. 北京: 国防工业出版社,1984: 64-72.Lin Mao-yong and Ke You-an. The Theory of Radar Signals[M]. Beijing: National Defense Industry Press, 1984:64-72.

[11] Steven M key. Fundamentals of Statistical Signal Processing,Volume II: Detection Theory [M]. New Jersey: Prentice Hall Press, 1998: 261-271, 279-296.