一种基于散焦偏移差的全带宽机载SAR动目标检测方法

许睿鹏 仇晓兰 胡东辉 丁赤飚

①(中国科学院电子学研究所 北京 100190)②(中国科学院研究生院 北京 100190)③(中国科学院空间信息处理与应用系统技术重点实验室 北京 100190)

1 引言

合成孔径雷达(Synthetic Aperture Radar,SAR)是一种全天时、全天候的高分辨率微波成像雷达。它常用于对地面静止场景成像，但根据军事侦查与战场指挥的需要，获取场景中的运动目标具有重要的军事意义。因此，合成孔径雷达(SAR)动目标检测已成为SAR信号处理领域的一个重要发展方向。

在SAR动目标检测领域，目前主要包括单通道检测和多通道检测两大类方法。多通道检测方法主要包括相位中心偏置天线(DPCA)[1,2]技术，沿轨干涉(ATI)[3−5]技术以及空时自适应处理(STAP)[6,7]技术等。与单通道动目标检测方法相比，这些方法可检测速度范围大，杂波抑制能力强，但系统复杂度高，计算量较大。因此，如何挖掘单通道动目标检测方法的潜力，提高检测能力，仍是一个值得研究的问题。对于单通道检测方法来说，通常采取子视分解法[8−10]和频域滤波法[11,12]。子视分解法是利用子视间，静止目标和动目标偏移量不同的特点进行动目标检测，但由于每个子视只采用了部分带宽，其信杂比较低；频域滤波法是利用运动目标多普勒偏移的特性进行运动目标检测，它无法检测杂波频谱区内的运动目标，故可检测速度范围小。这些缺陷给两种算法的应用带来了一定的局限性。

本文提出了一种基于散焦偏移差的全带宽单通道机载合成孔径雷达动目标检测方法，该方法利用动/静目标存在多普勒中心频率差时，调频率偏差会引起动/静目标产生不同偏移量的特点，达到对消静止目标、保留动目标，进而完成动目标检测的目的。与传统的单通道检测方法相比，本方法在实现杂波对消的同时，利用动目标信号的全部带宽进行处理，可在对消后很好地保留动目标信号，故信杂比高、动目标检测能力相对更强。此外，该方法不受斜视角的限制，在正侧视及斜侧视时均可进行动目标检测，应用范围较广。

2 散焦偏移差检测动目标的原理和方法

2.1 斜视下的运动目标信号分析

图1给出机载斜视SAR和一个动目标的几何关系图。载机飞行速度为va，在t=0时刻，载机坐标为(0,0,h)，地面运动目标P位于(x0,y0,0)，定义0时刻目标的位置为其真实位置。P点到载机飞行航迹的最短斜距为到载机的斜距为目标方位向速度和加速度分别为vx和ax，距离向速度和加速度分别为和

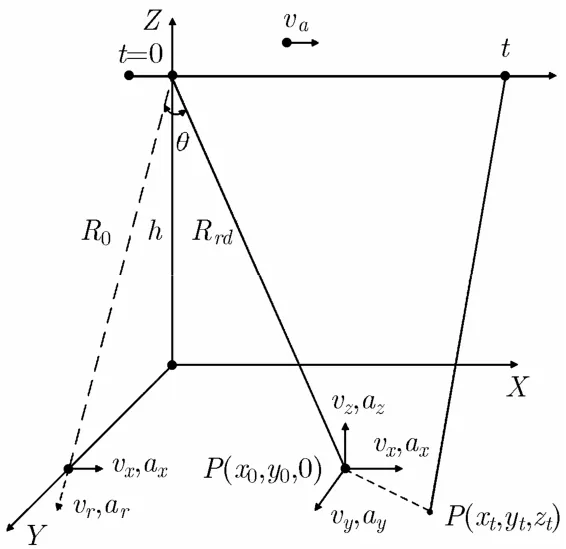
图1 回波几何模型

在t时刻，多普勒中心频率和调频率分别为

其中θ为斜视角。

在现有文献中[2,9]，通常不考虑距离和方位向加速度带来的影响，并且其信号模型常建立在正侧视的前提下(θ=0)，在此模型下可以将方位向和距离向速度对中心频率和调频率的影响分离(见式(2)和式(3))，便于对动目标进行参数估计。但在实际中，飞机在录取数据时常受到气流等诸多因素的影响，通常并非严格意义上的正侧视，故θ常不为0。因此分析斜视下的动目标信号模型，并研究相应的检测方法是具有实际意义的。

若不考虑距离和方位向加速度带来的影响(ar=0,ax=0)，则动目标中心频率和调频率可写为

由式(3)可知，当载机斜视角不为零时，目标的距离向速度会引起多普勒中心频率偏差，方位向速度不但会导致动/静目标之间存在多普勒调频率偏差，还会引入中心频率偏差。

2.2 基于散焦偏移差的动目标检测方法

设静止目标J和动目标T在t=0时刻均处于方位天线波束的中心，且静止目标的多普勒中心频率为fJc，方位向调频率为KJa，动目标的中心频率为fTc，方位向调频率为KTa，则静/动目标的零多普勒时刻分别为

静/动目标的方位回波信号可分别写为[13]

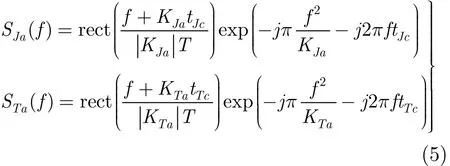
方位向匹配滤波器为

经方位匹配滤波后，静/动目标相位分别为

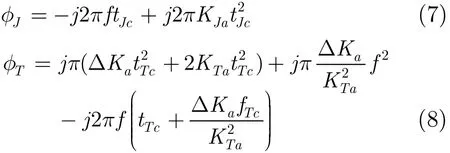
式(7)中的第1项表征静止目标位置的线性相位，该目标被压缩至t=tJc处。式(8)中的第3项表征运动目标位置的线性相位，该目标被压缩至t=tTc+(ΔKa/KTa)tTc处。可见，目标运动产生的调频率偏差ΔKa除了引起目标散焦外，还导致目标位置额外的偏移，偏移量为其与调频率偏差及中心频率成正比，与调频率的平方成反比。

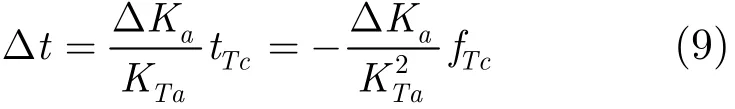
由上述现象同理可知，若在方位匹配滤波器中人为加入调频率偏差，可使目标成像后的位置发生偏移，且由于动/静目标中心频率、调频率不同，相同的调频率偏差将引入不同的偏移量。若采用调频率偏差分别为的滤波器进行方位压缩，两幅图像中的静止目标散焦程度相同，偏移量已知，可通过图像平移和插值完成对消。动目标因其偏移量与静止目标不同而无法完全对消，故该目标将得以保留。本文方法正是基于这一原理。

下面通过公式推导，给出动/静目标偏移量的计算公式，并进一步说明上述原理。

若采用调频率偏差分别为ΔK±的方位滤波器进行成像，静/动目标在两幅图像中的位置分别为

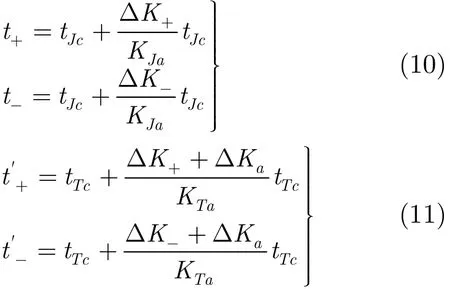
它们在两幅图像中的偏移量分别为

由式(12)和式(13)可知，动/静目标在两幅图像中的偏移量不同，偏移差为

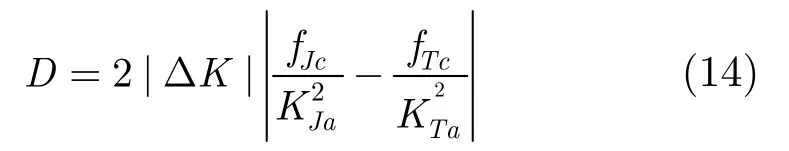
当以静止目标偏移量为标准进行图像平移后，动目标在两幅图像中仍存在大小为D的残余偏差，当静止目标对消后，运动目标由于存在偏移差而被保留。

根据上述原理，图2给出了基于散焦偏移差的动目标检测算法流程图。首先，对SAR回波数据做距离压缩、距离徙动校正，接着采用调频率偏差分别为ΔK±的滤波器进行方位压缩，成像后以一幅图像为基准，对另一幅图像进行插值和平移，再将两幅图像进行非相干对消，这样将有效地抑制杂波，提高数据的信杂比，最后利用恒虚警检测(CFAR)检测动目标。

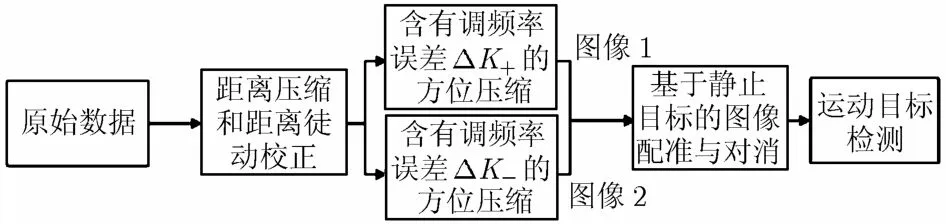
图2 算法的流程图

通过本节分析可知，本方法对全带宽进行处理，在对消静止目标的同时，动目标信号的能量可以更好地保留。子视分解法只利用动目标的部分带宽进行处理，故在消除静止目标的同时，其能量也下降了。因此，本算法的检测能力应高于子视分解法。

3 参数性能分析

在本节中，将从偏移差的影响因素、最小可检测速度和误差影响三方面对算法进行分析和论证。

本文方法主要利用动/静止目标的偏移差进行动目标检测。将它们的中心频率和调频率代入式(15)可得

其中l表示散焦长度。

(1)偏移差分析 由式(15)可知，D中第1项与系统参数相关；第2项与斜视角和动目标运动速度相关。下面以典型系统参数(载频f=5.3 GHz，平台速度va=150 m/s，中心斜距R0=20 km，调频率偏差ΔK =±0.5 Hz/s)为例，对式(15)中的各参数给偏移差带来的影响进行分析。

图3为在调频率偏差、斜距、波长已知的情况下，偏移差随距离向速度、方位向速度、斜视角变化的曲线图。由图3(a)可知，在小斜视角(θ＜5°)下，偏移差与sinθ成正比(见式(15))，故偏移差随斜视角近似线性增大。由图3(b)可知，当距离向速度大于0时，偏移差会随斜视角增大先减小后递增，并当斜视角(由式(16)推导得)时，偏移差等于零。

由上一节分析可知，偏移差(D)决定了动目标检测性能。但不能认为偏移差可以无限增大，这是因为动目标本身的散焦影响会对偏移差的选取产生限制。其原因有两点(1)偏移差是随调频率偏差增大而变大的，但调频率偏差的增大还会导致动目标散焦，能量下降；(2)若动目标的散焦长度超过了偏移差，对消会进一步减小其能量。由式(15)可知，在系统状态确定的情况下，调频率偏差ΔK±是影响偏移差和散焦长度的决定性因素。因此，在实际中对调频率偏差的选取需要权衡散焦长度和偏移差。

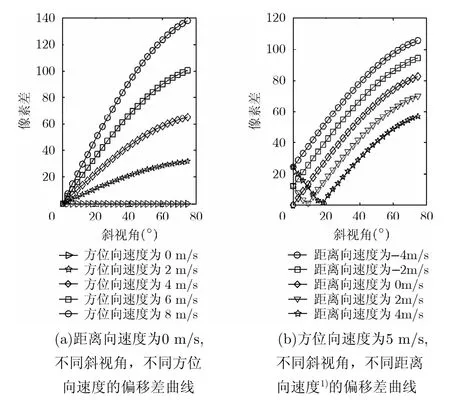
图3 偏移差随距离向速度、方位向速度和斜视角的变化曲线图

为了说明在不同的调频率偏差下，信杂比受到偏移差和散焦长度的影响，下面进行仿真如图4。仿真参数：载频f=5.3 GHz，平台速度va=95 m/s，中心斜距R0=20 km，调频率偏差ΔK=±0.5 Hz/s，目标的距离向速度1 m/s，方位向速度1 m/s。

图4中调频率偏差ΔK是从0.1 Hz/s到3 Hz/s变化的。由式(15)可知，目标的偏移差与调频率偏差成正比。在调频率偏差小于0.4 Hz/s时(区域1)，调频率偏差对偏移差的影响大于对散焦长度的影响，故对消后的信杂比是随调频率偏差的增大逐渐变大的。然而当调频率偏差大于0.4 Hz/s以后(区域2)，调频率偏差对散焦长度的影响超过了对偏移差的影响，这使动目标信号大部分被对消，信杂比骤然下降，影响其检测性能。因此，在实际系统中，需要针对不同的系统参数，选择恰当的调频率偏差ΔK 。

(2)最低可检测速度(MDV) 由式(4)，式(5)和式(15)可知，当飞机正侧视工作(即fJc=0)时，仅具有方位速度的目标无法引起中心频率偏差(即fTc=0)，此时D≡0。这时目标只存在像素内的幅度差，它易受杂波和噪声影响，难以检测。当飞机斜视工作时，具有方位向速度或距离向速度(或两者兼有)的目标导致偏移差不为零，易于检测。由式(15)得到其最低可检测速度为

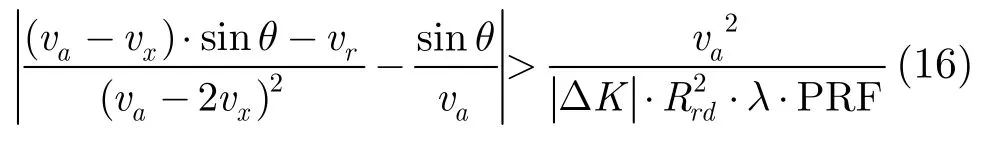
根据式(16)可知，最低可检测速度与调频率偏差、斜距、波长和斜视角有关。图5为通过仿真得到可检测门限随斜视角的变化曲线。

由图5可知，当斜视角为0°时，仅有方位向速度的目标因其只存在幅度差而难以被检测。随着斜视角的增大，方位向最低可检测速度的下限不断降低，因为斜视角越大，相同方位速度引起的中心频率偏差越大(见式(4))。可知，本方法不仅可以用于斜视情况下，而且随着斜视角的增大，最小可检测速度范围也将进一步扩大。

(3)系统调频率误差的影响 在本文方法中，杂波对消的基础是建立在调频率偏差ΔK±所成的两幅图像中静止目标具有相同散焦特性之上的。但实际使用的多普勒调频率总会存在误差，此时将引起静止目标对消不完全，导致信杂比的下降。图6给出了信杂比与系统调频率误差的关系曲线。

由图6可知，就总体趋势而言，系统调频率误差越大，信杂比越低。然而对于一般的SAR成像系统来说，调频率误差通常小于1%，这时，信杂比最低下降至21.1 dB(见图6虚线)，运动目标仍可被检测，故本文方法具有很好的鲁棒性。

4 仿真实验

为了验证本文方法的有效性，运用其对仿真数据进行动目标检测。仿真参数如下：载频f=5.3 GHz，平台速度va=150 m/s，中心斜距R0=20 km，调频率偏差ΔK=±0.5 Hz/s，斜视角θ=0.5°，为使仿真更具真实性，采用公路场景的实际SAR图像作为背景，在公路上添加了4个运动速度不同的目标，目标能量峰值为0.2，噪声服从高斯分布，动目标参数见表1。

表1 运动目标参数

在图7(a)中，方框表示了动目标的原始位置，它们均位于公路上。而圆圈则表示由运动而导致的实际成像位置。图7(b)为CFAR检测结果，由图可见，本文方法可检测到3个目标，目标4无法检测。这是因为目标4与静止目标的偏移差小于1个像素(由式(15)计算可得)，动/静无法有效的分离，故在静止目标对消的同时，该目标也被对消了。

图8为目标2所在距离门对消前后的结果。由图8(a)可见，目标2完全被杂波所淹没，根本无法检测。经杂波对消后，目标2的信杂比得到了大幅提高，可准确的检测到目标(见图8(b))。

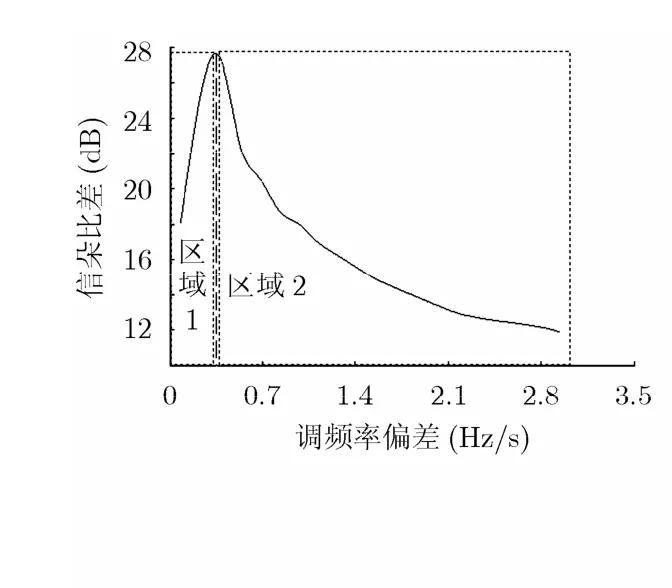
图4 信杂比随偏移差变化曲线

图5 最低可检测速度门限

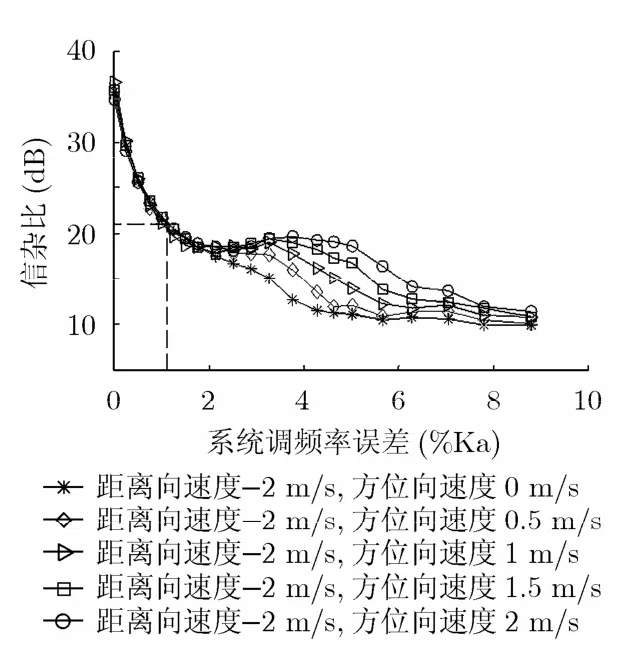
图6 调频率误差与信杂比的关系

图7 动目标检测结果

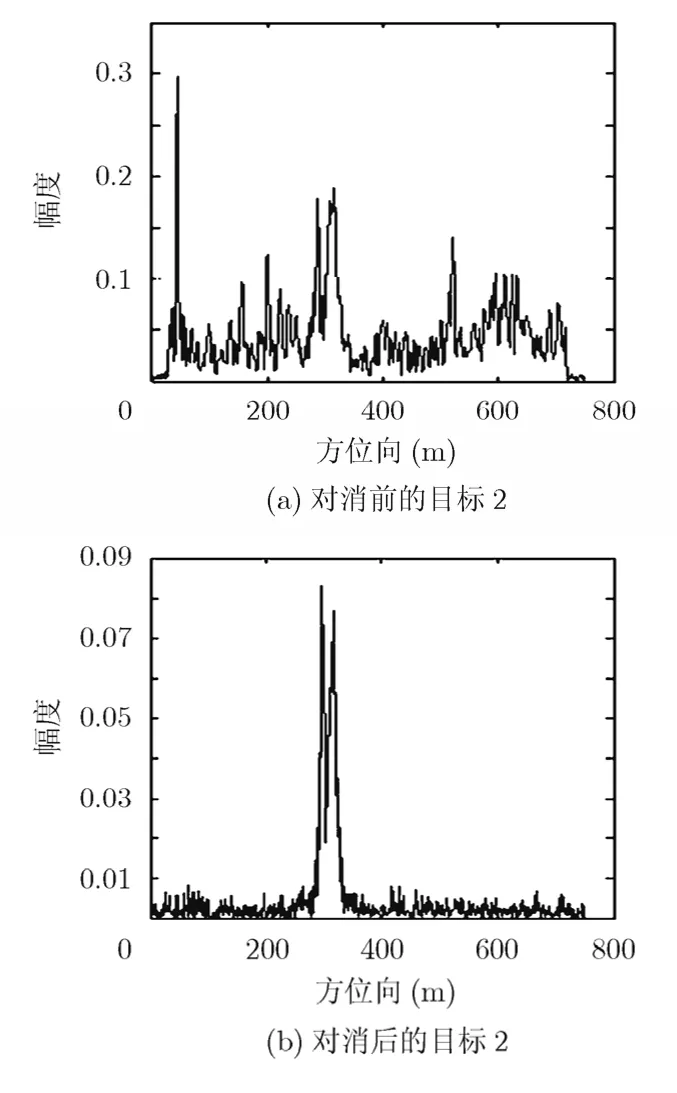
图8 距离门对消前后目标2的检测结果

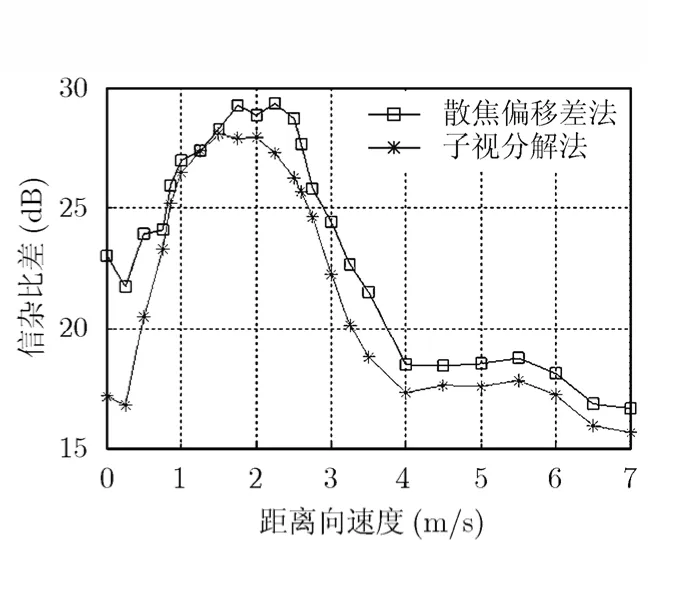
图9 对消前后信杂比差

下面对本文方法的检测性能进行进一步仿真试验。由于方法的检测性能直接受到对消后的信杂比影响，下文将在典型距离向和方位向速度条件下，对本文方法和子视分解法(两视)进行仿真，仿真参数同上，动目标方位向速度vx=1 m/s。得到杂波对消前后信杂比增强曲线图。

由图9可见，当距离向速度为1-1.4 m/s的时候，子视分解法与本文方法得到的结果相近，这是由于目标距离向速度的变化，使得频谱移动，在子视处理的时候，动目标信号几乎集中在其中的一视中，正是利用能量分布的不均匀性，信杂比才可在对消后大幅提高，与本文方法接近。但从总体上看，在不同速度的情况下，利用本文的散焦偏移差法所得到的曲线在对消前后信杂比差均高于子视分解法。这表明本文方法在对消后，更好的保留动目标信号，故其具有更强的检测能力。

5 结束语

本文提出了一种基于散焦偏移差的全带宽单通道机载运动目标检测的方法。该方法是依据在散焦情况下运动目标和静止目标的偏移不相同，将两幅图像进行配准并对消静止目标保留运动目标，进而检测运动目标。本文给出了算法性能的详细分析，并通过仿真实验验证了本算法的有效性和优越性。

[1] Wang H S C. Mainlobe clutter cancellation by DPCA for space-based radars[C]. IEEE Aerospace Applications Conference Digest, Crested Butte, Colorad, USA, February 3-8, 1991: 1-10.

[2] 郑明洁, 杨汝良. 一种改进的DPCA运动目标检测方法[J].电子学报, 2004, 32(9): 1429-1432.Zheng Ming-jie and Yang Rui-liang. An improved DPCA moving targets detecting algorithm [J]. Acta Electronica Sinnca, 2004, 32(9): 1429-1432.

[3] Sikaneta I and Gierull C H. Ground moving target detection for along-track interferometric SAR data[C]. IEEE Aerospace Conference, Big Sky, Montana, USA, Mar. 6-13,2004: 2227-2235.

[4] Chapin E and Chen C W. Along-track interferometry for ground moving target indication [J]. IEEE Aerospace and Electronic Systems Magazine, 2008, 23(6): 19-24.

[5] Gierull C H, Maori D C, and Ender J. Ground moving target indication with tandem satellite constellations [J]. IEEE Geoscience and Remote Sensing Letters, 2008, 5(4): 710-714.

[6] Klemm R. Introduction to space-time adaptive processing [J].Electronics & Communication Engineering Journal, 1999,11(1): 5-12.

[7] Klemm R and Ward J. STAP I-Architectures and algorithms[C]. IEEE Radar Conference, Rome, Italy, May 26-30, 2008: 1-2.

[8] Kirscht M. Detection and imaging of arbitrary moving targets with single-channel SAR [J]. IEE Proc.-Radar Sonar Navigation, 2003, 150(1): 1984-1992.

[9] Liu Shu-jun, Yuan Yun-neng, Gao fei, and Mao Shi-yi.Method of moving target detection based on sub-image cancellation for single-antenna airborne synthetic aperture radar [J]. Journal of System Engineering and Electronics,2007, 18(3): 448-453.

[10] 张露, 郭华东, 韩春明, 周平. 基于子孔径分解的SAR动目标检测方法[J].电子学报, 2008, 36(6): 1210-1213.Zhang Lu, Guo Hua-dong, Han Chun-ming, and Zhou Ping.Moving targets detection in SAR images based on sub-aperture decomposition [J]. Acta Electronica Sinica, 2008,36(6): 1210-1213.

[11] Raney R K. Synthetic aperture imaging radar and moving targets [J]. IEEE Transactions on Aerospace and Electronic System, 1971, 7(3): 499-505.

[12] Freeman A and Currie A. Synthetic aperture radar images of moving targets [J]. GEC Journal of Research, 1987, 5(2):106-115.

[13] Cumming I G and Wong F H. Digital Processing of Synthetic Aperture Radar Data Algorithm and Implementation [M].New York, Artech House, 2007: 89-105.