基于角度余切值的多被动传感器数据关联

田 野 姬红兵 欧阳成

(西安电子科技大学电子工程学院 西安 710071)

1 引言

由于被动传感器不向外辐射电磁波，与主动传感器相比具有抗干扰能力强，隐蔽性好等优点，因而国内外越来越多的学者开始致力于这方面的研究，与之相关的成果也日益增多[1−9]。在被动多传感器系统中需要解决的一个关键问题就是量测数据的关联，即确定哪些量测来源于同一目标。由于采用被动定位，传感器仅能获取目标的方位角和俯仰角信息，在对多个目标进行交叉定位时，不同的定位线将产生大量的虚假定位点。另外，由于目标漏检、虚警等情况难以避免，如何快速有效地排除虚假点，进而得到正确关联已成为众多学者研究的重点。

通常，被动多传感器数据关联可以描述为多维分配问题，用穷举法求其最优解是一NP-hard问题，计算复杂度随问题维数的增加呈指数增长。针对这一问题，人们提出各种次优算法，如拉格朗日松弛算法[1]等，但这些算法都难以在给定的时间内得到满意解。文献[2]提出的关联矩阵分析法采用指示函数替代多维分配，在一定程度上提高了运算速度，但它仍是基于视线距离的算法[2,6,9]，而这类算法必须将角度换算成距离，且包含大量的矩阵运算和求偏导运算，限制了运算速度的进一步提高。因此，本文提出一种新的思路，首先，直接利用角度信息，合理构造检验统计量，然后通过方位角检测和俯仰角检测得到可能的候选关联集，进而采用指示函数法对候选关联集进行分析，挑选出正确的关联组合。

2 基于角度余切值的数据关联

设有3个传感器S1, S2, S3，对于目标T的定位线的空间位置关系如图1所示。当没有量测误差时3条定位线在空间中以及在3个传感器构成平面内的投影都应交于一点。然而，当存在量测误差时，3条定位线及其对应的投影线均无法交于一点。这种偏差可以理解为两种形式，一是方位角引起的偏差，二是俯仰角引起的偏差，如图2所示。因此，下面针对这两种形式的偏差分别采用方位角检测和俯仰角检测进行处理。

图1 三视线交叉

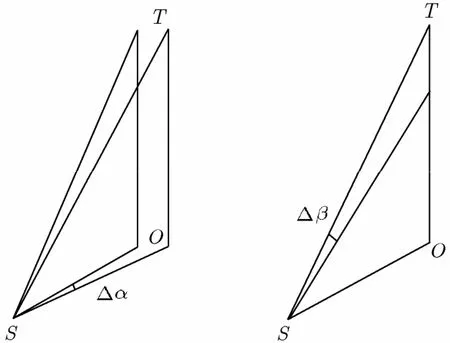
图2 两种形式的偏差

2.1 方位角检测

图3示出了无量测误差时在3个传感器构成的平面内3条定位线的投影几何关系。为简单起见，假定∠S1S3S2=θ,=L13,=L23,以的指向作为方位角的零度参考线。在ΔS1S3O和ΔS2S3O 中利用正弦定理可以求得3条投影线的长度,以及，进一步可以得到3个方位角所必须满足的关系(推导略)：

如果存在量测误差，则式(1)右端不为0，构造检验统计量如下：

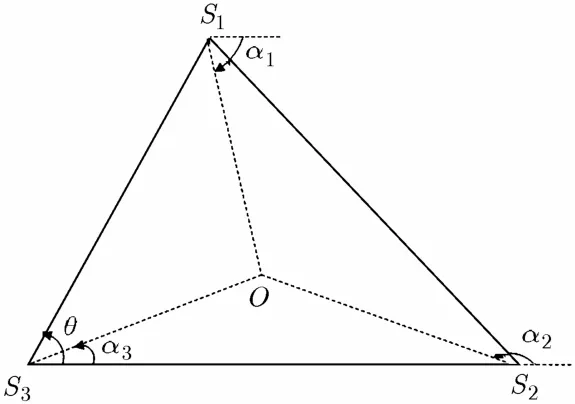
图3 3视线交叉投影

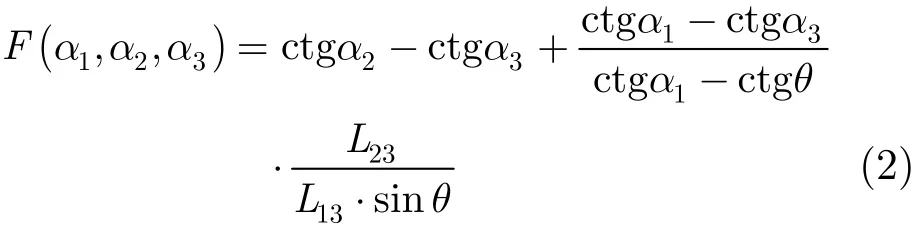
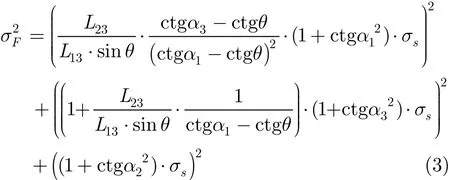
其中σs为传感器量测噪声标准差。

若检验统计量落在置信区间内，则认为该候选关联可能属于同一目标，予以保留；否则，为错误组合，予以删除。由检测统计量及其方差的表达式可以看到，仅依靠角度信息的余切值便可以进行检测，避免了传统基于视线距离的方法将角度信息转换为距离信息带来的计算量增加。

下面以3个传感器系统为例说明以上检测方法：首先，将各个传感器获取的方位角进行编号，,i=1,2,3表示第i个传感器的第j个方位角量测；然后，列举所有的可能关联组合，分别计算相应的检验统计量，例如对于[,,]，直接计算方位角的余切值，利用式(6)和式(7)求得F(,,)及其相应的标准差σF；最后设定置信区间为[−3σF,3σF]，从而保证其置信度不低于0.997，筛选符合要求的关联组合。

2.2 俯仰角检测

由于量测误差的存在，使得定位线在垂直于投影面方向上的高度不等，通过检测各个定位线高度的差别可以挑选出可能的关联组合。图4和图5显示了定位线高度的空间几何关系，利用三角关系很容易得到以下4个高度(推导略)：

图4 S1,S3传感器视线高度

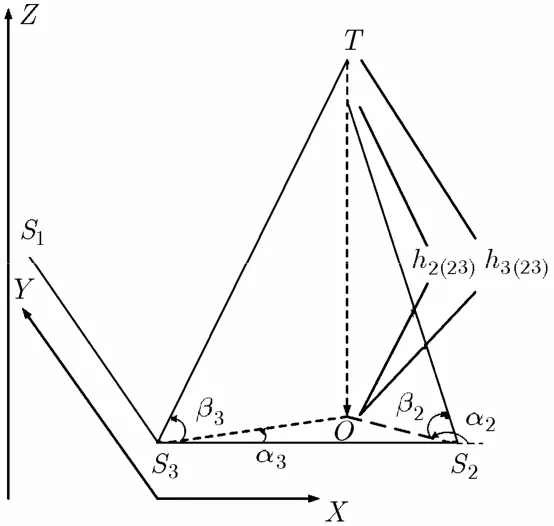
图5 S2,S3传感器视线高度

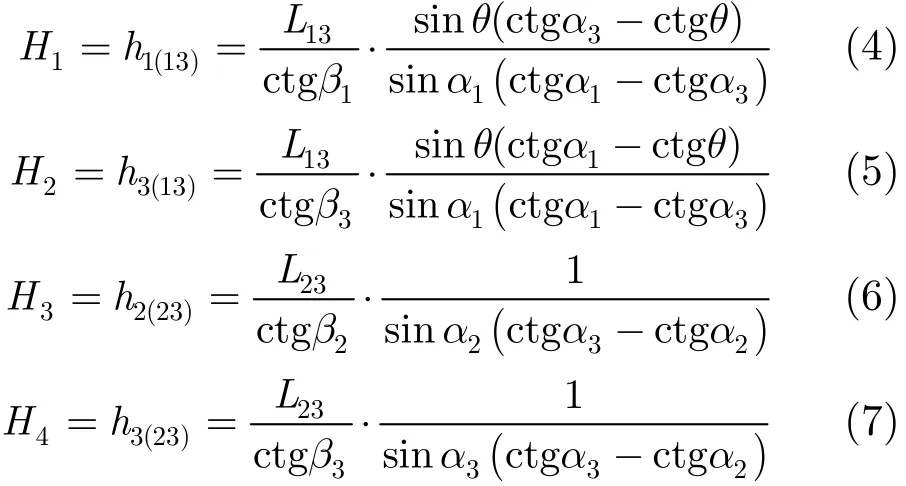
其中hk(ij)表示由传感器i和j确定的第k个传感器定位线的高度。

取以上4个高度中的任意两个之差作为检验统计量：

该统计量近似服从零均值的高斯分布，其方差由式(9)给出

其中i, j=1,2,3,4，i＞j，m, n=1,2,3，m≠n，σs为传感器量测噪声标准差。

同样，若检验统计量落在置信区间内，则认为该候选关联可能属于同一目标，予以保留；否则，为错误组合，予以删除。

以3.1节中的情况为例：首先将各个传感器获得的俯仰角进行编号，,i=1,2,3表示第i个传感器的第j个俯仰角量测，并与方位角检测中的编号相对应；然后列举所有的可能关联组合，分别计算相应的检验统计量，例如对于[,,]直接将其转换成角度余切值，利用式(4)-式(9)求得6个检测量eij,i, j=1,2,3,4;i＞j 和相应的标准差σeij,i, j =1,2,3,4;i＞j；最后设定置信区间为[−3σeij,3σeij]，筛选符合要求的关联组合。

2.3 指示函数法

文献[2]提出一种关联矩阵分析方法替代传统的m-D分配法，有效提高了关联效率。它建立在以下两个假设基础之上：

假设1 每个传感器量测源于且仅源于1个目标或1个杂波；

假设2 每个传感器量测只能和其他传感器量测关联1次。

在此基础上，对于候选关联集，建立指示函数

其中i=1,2,3，n=1,…,ni，m为可能候选关联的总数。

如果ξ(sin)等于0，则说明第i个传感器的第n个量测不与其他两个传感器的量测进行关联；如果ξ(sin)等于1，则说明第i个传感器的第n个量测只能与其他两个传感器的某两个量测关联；如果ξ(sin)大于1，则利用代价函数选取一个正确的关联组合。

本文选用俯仰角检测中高度差的绝对值平均作为代价函数，该代价函数越小说明偏差越小，则3条定位线源于目标的可能性越大。代价函数如下

其中c表示高度差的总个数。

假设通过方位角和俯仰角检测后得到的候选关联集如下：

其中矩阵行代表某种量测组合，列代表不同的传感器。

具体分析步骤如下：情况1：当∃ξ(sin)=1时：

(1)如果ξ(sin)=1，Pri=n，r=1,…,m ，将第r种关联放入正确关联矩阵Z中，并令Pr1=Pr2=Pr3=0；

(2)如果ξ(sin)=1，Pri=n，Ptj=Prj，j=1,2,3,j≠i, r=1,…,m, t=1,…,m, t≠r ，则令Pt1=Pt2=Pt3=0；

(3)如果∃ξ(sin)=1，i=1,2,3,n=1,…,ni，返回步骤(1)和步骤(2)，否则执行步骤(4)；

(4)重新计算ξ(sin)，如果∃ξ(sin)=1返回步骤(1)，如果∃ξ(sin)=0，则所有的正确关联组合已经找到，关联完成。

情况2：当ξ(sin)＞1或ξ(sin)=0时：

(1)计算代价函数E=Ψ(Pr)，Pr=[Pr1Pr2Pr3]，r=1,…,m ，Pr1＞0，Pr2＞0，Pr3＞0，El=min(Er＞0)，r=1,…,m ，P矩阵的第l行放入正确关联矩阵Z中，并令Pl1=Pl2=Pl3=0；

(2)如果Pwj=Plj，j=1,2,3,w≠l, w=1,…,m ，则令Pw1Pw2Pw3=0，El=0；

(3)返回步骤(1)和步骤(2)，直到∀Puv=0,u=1,…,m, v=1,2,3。

2.4 算法步骤

步骤1 初始化。计算各个传感器获取的所有量测的余切值[ctg,ctg]，其中[,]表示第i个传感器的第j组量测；

步骤2 方位角检测。利用方位角余切值，计算各种关联组合对应的统计量F，设定置信区间为[−3σF,3σF]，保留通过检测的关联组合，放入候选关联集Q；

步骤3 俯仰角检测。利用俯仰角余切值，计算候选关联集Q中各种关联组合对应的统计量eij,i, j=1,2,3,4;i＞j ，设定置信区间为[−3σeij,3σeij]，保留通过检测的关联组合，放入候选关联集P；

步骤4 候选关联集分析。利用指示函数和代价函数，分析候选关联集P，得到最终的正确关联组合。

3 仿真结果与分析

为了说明本文算法的优势，将其与经典的拉格朗日松弛算法[1]以及文献[2]中所提方法进行对比。仿真实验采用3个传感器观测空中的5个目标，量测包含方位角和俯仰角。3个传感器的位置分别为：s1(0,10,0),s2(10,0,0),s3(0,0,0)，方位角和俯仰角的量测噪声标准差均为σs。目标分水平编队和十字编队两种情况，目标间距均为d。水平编队目标位置：目标1(5,5,1)，目标2(5+d ,5,1)，目标3(5−d,5,1)，目标4(5+2d,5,1)，目标5(5−2d,5,1)；十字编队目标位置：目标1(5,5,1)，目标2(5+d ,5,1)，目标3(5−d,5,1)，目标4(5,5+d ,1)，目标5(5,5−d ,1)，单位均为km。以下表中均为100次Monte Carlo仿真结果平均，其中t表示1次仿真的运行时间，p表示关联正确率。

表1和表2为无杂波环境的情况，检测概率Pd=1。可以看出当目标间距大于1 km时，文献[2]中算法和本文算法的关联正确率与拉格朗日松弛算法接近，但是运行时间大大缩短，本文算法比文献[2]算法在速度上也提高了近7倍。表1中由于目标分布情况比较简单，正确率普遍较高。表2中当目标间距为0.5 km时，本文算法正确率略差于拉格朗日松弛算法，但仍高于文献[2]算法。

表3和表4为杂波环境的情况。检测概率Pd=0.95，虚警率Pf=0.05，杂波产生区域的大小为0.1rad×0.1rad 。从表中可以看出，受漏检和虚警的影响，与无杂波环境相比，关联正确率均有所下降，且随着目标间距的减小，关联正确率呈递减趋势，但本文算法的性能仍高于文献[2]所提方法。

综上所述，本文方法的主要优势在于以角度余切值替代传统的视线距离构建统计量，从而有效提高了关联速度，两次检测筛选掉的候选关联越多，关联速度也就越快。值得注意的是，由于检测统计量的方差采用了余切值的一阶泰勒级数展开近似，量测误差越大，这种近似的偏差也就越大，所以当目标间距较小时，关联正确率的下降较为明显。

4 结论

在被动多传感器系统中，至少需要两个以上的传感器联合才能完成目标定位，所以在进行定位之前，必须确定多个传感器的量测数据是否来自同一目标。本文针对该问题进行了研究，分析了基于角度余切值的快速关联算法。该算法采用角度余切值替代传统的视线距离构造检验统计量，通过方位角和俯仰角两次检测筛选候选关联，利用指示函数法对候选关联集进行分析，从而在保证关联正确率的前提下极大地提高了关联效率。实验结果表明，本文所提算法关联正确率高，关联速度快，是一种适合工程应用的关联算法，具有一定的应用价值。

表1 无杂波环境下水平编队

表2 无杂波环境下十字编队

表3 杂波环境下水平编队

表4 杂波环境下十字编队

[1] Pattipati K R, Deb S, and Bar-Shalom Y, et al.. A new relaxation algorithm and passive sensor data association[J].IEEE Transactions on Automatic Control, 1992, 37(2):198-213.

[2] Liu Hang, Dou Li-hua, Pan Feng, and Dong Ling-xun.Research on data association in three passive sensors network[C]. IEEE International Conference on control and Automation, May 30-June 1, Guangzhou, China, 2007:3235-3238.

[3] Deb S, Yeddana Pud I M, and Pattipati K R. A Generalized S-D assignment algorithm for multisensor-multitarget state estimation[J]. IEEE Transactions on Aero space and Electronic Systems, 1997, 33(2): 523-537.

[4] Ruan Yanhua, Willett P, and Streit R. Comparison of PMHT and S-D assignment Trackers[C]. Proceeding of the 1999 SPIE Conference 3720, Orlando FL, April 1999.

[5] Kaplan L M, Bar-Shalom Y, and Blair W D. Assignment costs for multiple sensor track-to-track association[J]. IEEE Transactions on Aerospace and Electronic Systems, 2008,44(2): 655-677.

[6] 刘宗香, 谢维信, 杨焕. 被动传感器系统分层快速关联算法[J].电子学报, 2004, 32(12): 2038-2040.Liu Zong-xiang, Xie Wei-xin, and Yang Huan. Hierarchical fast data association in the passive sensor system [J]. Acta Electronica Sinica, 2004, 32(12): 2038-2040.

[7] 周莉, 李洪波, 杨秀珍, 何友. 多被动传感器系统四时差量测数据关联算法[J]. 哈尔滨工业大学学报, 2009, 41(3): 190-192.Zhou Li, Li Hong-bo, Yang Xiu-zhen, and He You. Four-TDOA data association algorithm for multi-passive-sensor system [J]. Journal of Harbin Institute of Technology, 2009,41(3): 190-192.

[8] 修建娟, 何友, 车志宇, 修建华. 三维测向无源定位中的数据关联算法研究[J]. 系统工程与电子技术, 2009, 31(2): 329-332.Xiu Jian-juan, He You, Che Zhi-yu, and Xiu Jian-hua. Study on bearing measurements association algorithm in 3D passive location systems [J]. Systems Engineering and Electronics,2009, 31(2): 329-332.

[9] 李良群, 谢维信, 黄敬雄, 郝润泽. 被动传感器阵列中基于视线距离的数据关联[J]. 系统工程与电子技术, 2009, 31(4):952-955.Li Liang-qun, Xie Wei-xin, Huang Jing-xiong, and Hao Run-ze. Data association based on line-of-sight range in passive sensor array [J]. Systems Engineering and Electronics,2009, 31(4): 952-955.