基于多分辨率信号分解的低轨通信卫星频谱感知

马 陆 李理敏 胡泽鑫 梁旭文

(上海微小卫星工程中心 上海 200050)(中国科学院上海微系统与信息技术研究所 上海 200050)

1 引言

认知无线电技术是为了解决频谱资源日趋紧张与实际利用率低下之间的矛盾而提出的。这一矛盾不仅在地面通信系统中存在，而且在卫星通信系统中也是一个棘手的问题。特别是低轨通信卫星(LEO)在一个回归周期内星下点覆盖地球表面大部分地域，其频谱环境的复杂性远甚地面移动设备。以UHF和L频段(300 MHz-2 GHz)为例，从ITU给出的频谱划分可见，当前的频率空间已经非常拥挤，而实际使用中的实测效率大部分不足一半，有部分甚至不到5%[1]，可见认知无线电技术应用于卫星通信是有着广阔应用前景的。作为认知无线电的基础，近年来诸多文献针对频谱感知技术进行了探讨。提出了大量的算法如匹配滤波器、能量检测、循环平稳检测，本振泄露检测等[2]。其中能量检测虽然精度不高但是计算复杂度低，因此为IEEE802.22[3]，MUOS[4]等系统采用。本文拟在卫星上行链路实现频谱感知，由于对多地域宽频带都要完成检测，所以也采用能量检测作为感知手段。

在能量检测中如何选择分辨率是提高检测精度的关键之一，分辨率过大会使可能存在的频谱空穴无法检测到，分辨率过小则增加了计算量并且会将信号的频域抖动误判为空穴。另一方面为了完成多星地面综合判决过程，感知结果需要发送到地面站，因此压缩感知数据将大幅提高星间链路和下行馈电链路的利用效率。

本文结合多分辨率信号分解技术，将高斯金字塔分解应用于频谱数据量的压缩，将拉普拉斯金字塔分解应用于频谱空穴的检测，并模拟一个0-100 kHz的包含20个频谱空穴的信号源进行仿真。经过仿真证明感知数据量获得了大幅压缩并能精确地检测频谱空穴的数量和位置。

本设计着眼于某卫星系统的实际环境，以最终星上应用为目的。在下文中首先介绍当前常用的一些频谱检测方法及各自的优缺点，然后探讨了信号多分辨率分解的数学理论基础，接下来论述应用于低轨卫星通信中的多分辨率信号分解频谱感知算法，最后给出性能的定量仿真及结论。

2 频谱检测的方法

频谱检测的目的是为了在当前的射频环境中寻找未知参数的值，这些未知参数包括信号数量及其带宽，频带间距，平均功率，调制类型和传输时间等[5]。下文将给出一些常用的检测方法以及各自的优缺点。

(1)固定分辨率无参谱估计 固定分辨率无参谱估计[6]将频谱的估计值与门限进行比较从而获得对感兴趣的频带(Band-Of- Interest，BOI)的检测结果，是一种比较简单的频谱检测方式。固定分辨率无参谱估计使用固定的带宽分割待测频谱，并对带内能量进行累积，依据固定门限进行判别。在MUOS卫星系统中，假设空穴带宽大小之比约15 dB，在10 dB的信噪比环境下固定分辨率无参谱估计给出的空穴数量仅有实际数量的1/4左右，可见漏检概率很高。

(2)多渐进无参谱估计 文献[7]提出了多渐进无参谱估计，它被用于多感知器的认知无线电环境中，对每一个BOI会得到一个由频谱估计值构成的矩阵，由此通过统计得到频谱空穴。此算法虽然精度高，但是复杂度也很大。受到卫星的硬件复杂度限制，难以在星上实现多个感知器以完成谱估计矩阵的构造，因而多渐进的谱估计方式也不适用。

(3)小波谱估计 小波分析也可应用于BOI检测，但是由于卫星频谱感知覆盖范围大，通信链路长，所以更多关心的是持续信号的存在，因此傅里叶变换比小波变换更好。而且卫星认知无线电中不需要多种谱估计，因为主要关注的是空穴是否存在，不考虑具体信号特征。所以小波谱估计在卫星频谱感知中并不适用。

(4)形态滤波器 在文献[8]中使用形态滤波器进行底噪估计，它可以在分析的带宽之间平滑变化。但是由于第1步采用了固定分辨率的无参谱估计同样会产生无法匹配所有BOI带宽的问题，并且这一算法主要关注的是底噪的估计而不是频谱空穴的位置，因此也不适用于卫星频谱感知。

3 多分辨率信号分解

多分辨率分析就是在不同的尺度下研究信号，而分辨率可以理解为表征信号时单位长度所需的样本数。从低分辨率信号开始获得场景的概貌，然后有选择的提高分辨率以采集所需要的细节特征[9]。

3.1 分析和综合

多分辨率信号分解在每一级需要制定一系列的信号域以及在不同分辨率之间映射信息的分析综合算子。分析算子用于减少信息而综合算子应设计为尽可能地恢复信息[10]，因此信号的分解和还原可以表示为，其中的箭头表示在金字塔中从高到低或从低到高的行进方向。

式(1)表明分析过程中，Vi中元素与Vj中元素的映射关系，式(2)表明综合操作中元素的映射关系，因此完整的组合操作如式(3)所示，从第i阶到第j阶再回到第i阶：

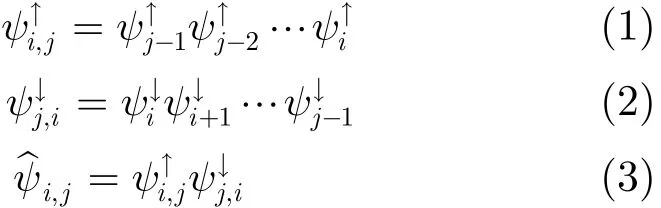
由于分析操作在分解过程对信号信息的减少是不可逆的，不可能借助综合操作完整重建，因此式(3)的结果实际是对第i阶实际值的近似。

3.2 线性塔式变换

如前所述分析再综合的结果只能是对实际值的近似，所以如果需要完全的重建，在对信号分析之后还需要进行扩展。

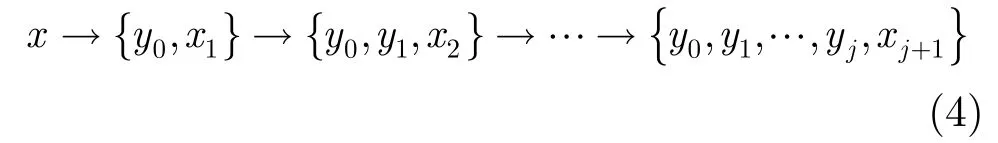
由式(4)可见信号x可以由xj+1和y0,y1,…,yj直接进行重建：

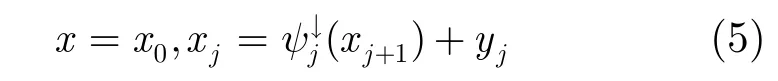
式(4)中的信号分解过程即为信号x的金字塔变换过程，式(5)中所示的信号重建过程即为金字塔逆变换，图1表明了3阶金字塔变换和金字塔逆变换的过程。

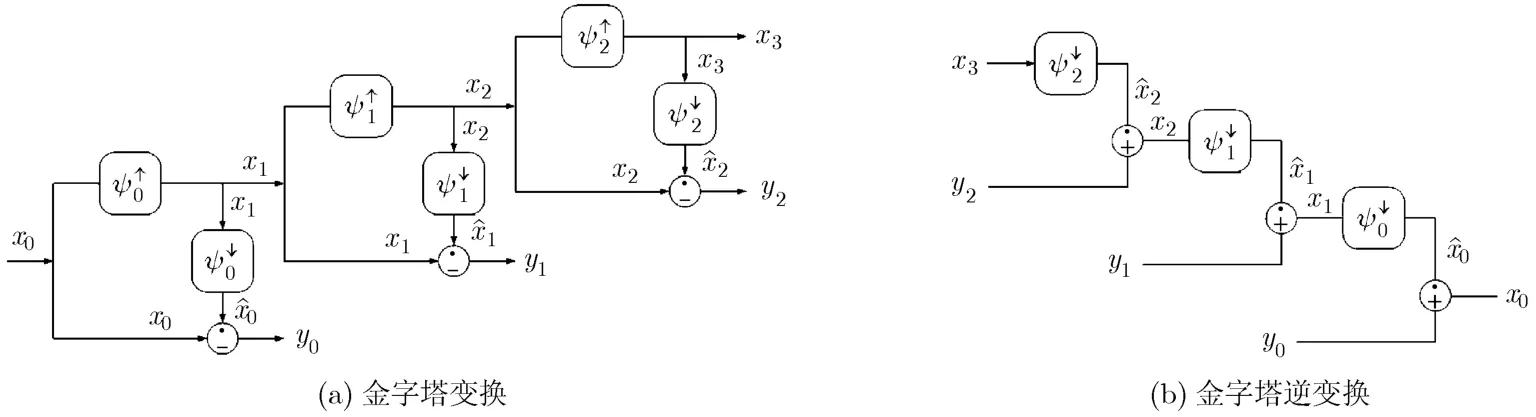
图1 3阶塔式变换及逆变换

4 基于多分辨率信号分解的频谱检测

为了在某卫星系统中实现反向链路的频谱感知过程，需要最大程度地减小数据量可以减轻对馈电链路和星间链路的占用率；另一方面需要一个快速高效的检测算法。本文提出一种基于Burt-Adelson[11]金字塔的能量感知算法，并利用多分辨率方式提高感知精度并加速收敛过程。

4.1 反向链路感知数据压缩

反向链路的数据压缩利用高斯金字塔实现，定义REDUCE过程，REDUCE(gj)为信号gj经过低通滤波器H1进行抽样运算，即gj+1= REDUCE(gj)。gj(j=0,1…,J)被称为逼近信号序列，也被称为高斯金字塔，J为给定的分解级数，g0为原信号(金字塔底)，则

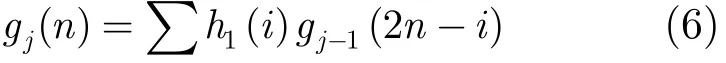
其中h1(i)是滤波器H1的冲激响应，由式(6)可知高一级的金字塔元素是由下一级金字塔中的元素经过加权求和得到的，元素个数从2N或者是2N+1减少到N个，如图2所示。可见每一次高斯塔式分解都可以将数据量压缩到原来的1/2。

图2 高斯塔式分解REDUCE及EXPAND过程

利用加权值表示式(6)为

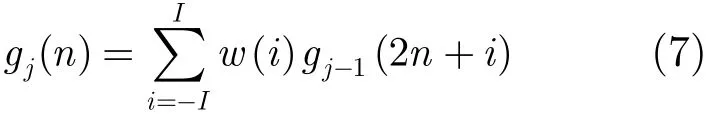
其中w(i)称再生核，选择滤波器长度为5，则w(i)应满足归一化，对称性及等贡献特性：

设定方程组求解，并根据再生核等贡献特性[11]定a=0.4，则b=0.25，c=0.05。

由于逐阶计算的方式速度低，不利于算法最终在星上系统的实现，在实际使用的时候并不需要逐阶计算，因此任意阶相对于0阶的1维REDUCE为

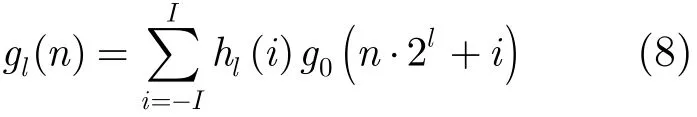
可以利用一组以倍频程下降的低通滤波器以减少采样间隔，实现快速滤波。

4.2 反向链路频谱空穴定位

本文将空穴的定位分成两步，首先是使用拉普拉斯金字塔分解对数据去抖动并且突出频谱信号功率突变点的位置，然后使用多分辨率分析流程对频谱空穴进行检测和识别。

4.2.1 感知数据拉普拉斯金字塔分解 在获得了任意阶的高斯金字塔分解之后，利用综合操作符可以获得原值的近似值，近似值与原值之差就是在分解过程中损失掉的细节，即拉普拉斯金字塔。

首先是对高斯金字塔变换后的数据进行插值，称之为EXPAND过程，主要是为了将gl扩展到和gl−1一样的长度，定义1维的EXPAND过程为

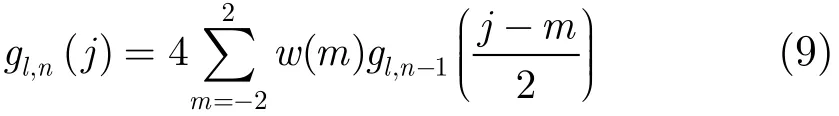
只有当(j-m)/2为整数的时候才会计算当前项的数值，图2中从上到下就表示了从gl,0到gl,1的变换过程，EXPAND过程的加权值与REDUCE过程中所使用的保持一致。

拉普拉斯塔式的定义就是原值与扩展值之间的残差，即

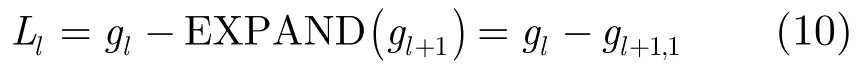
由于拉普拉斯金字塔比高斯金字塔少1阶，所以定义gN=LN。

经过拉普拉斯金字塔变换后，信号的功率谱密度函数表现为一系列不同分辨率的信号细节，这种表达是稀疏的，而且在每次EXPAND和做差的过程中，边缘或者是跳变点的变化会愈发明显，因此，对误判有很好的抑制，在后面的仿真中会证明这一点。

4.2.2 多分辨率频谱感知算法流程 信号数据经过拉普拉斯塔式变换之后，需要使用多分辨率算法对其进行分析。多分辨率是在固定分辨率频谱分析的基础上加上尺度变换实现的，外循环选取时间序列的中一部分时间点进行运算并统计综合，内循环在不同频域尺度下进行固定分辨率频谱检测，并在输入数据的PSD上进行比较判决，因此获得的数据结果优于固定分辨率频谱感知。图3表明了这一过程。

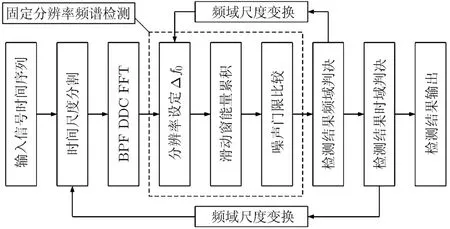
图3 多分辨率频谱感知算法流程

首先考虑固定分辨率的噪声门限选取，在AWGN信道条件下检测概率和虚警概率可以表示为[2]

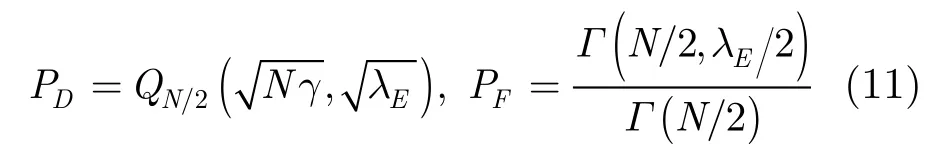
其中Γ(˙)是伽马函数，Qm(˙)是Marcum函数，N采样点数，λE为噪声门限。根据恒虚警(CFAR)准则，固定虚警概率PF就可以得到判决门限λE。

时间尺度的变换是为了计算统计均值，频域尺度变换才是为了寻找最合适的能量累积窗宽度，这里主要考虑频域尺度变换。首先自由选取，如W/10(W为总感知带宽)作为初始Δf0。在进行了一次固定分辨率频谱检测后，选取初始Δf0的1/2再次做检测，如此往复直到检测结果无论是空穴数量还是判定的空穴位置都相对稳定，则判定为收敛，并将空穴的位置作为结果输出。

然后选取下一个时间序列求出空穴结果并重复过程以求统计均值作为最终结果输出。

5 仿真与分析

根据某卫星系统实际应用中的感知步长，假设星上原始的感知带宽为100 kHz，经过下变频到零中频后采样，共有32768个采样点，其中的频谱空穴共有20个。图4给出了此信号的功率谱密度，后续的仿真和分析都基于此进行。高斯金字塔和拉普拉斯金字塔的再生核根据再生核等贡献特性[11]选择为a=0.4,b=0.25,c=0.05。

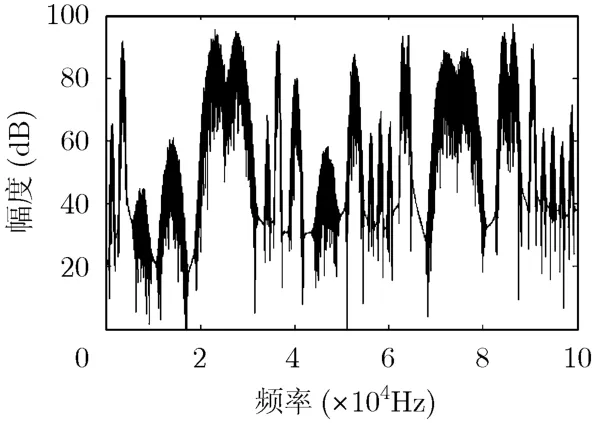
图4 星上原始采样数据PSD

5.1 高斯塔式分解采样数据压缩

低轨通信卫星进行频谱感知后需要在地面进行合判决，因此需要降低数据量以提高链路的利用效率。特别地，在低轨卫星高动态条件下，可以提高频谱感知的响应时间。高斯塔式分解在对频谱数据进行采样后可以将数据采样点数压缩到原来的1/2N(N=1,2…)，并且最大程度地保持着数据原有的形状。

如图5所示，从原数据32768点进行数据压缩，经过7次高斯金字塔变换所得的数据基本保持了原有的信号轮廓，数据量下降了128倍，但是直接进行256点采样的数据损失了大量的原信号细节，经过仿真计算，直接256点采样和7阶Gaussian金字塔压缩(256点)各自相对于16384点直接采样数据的均方误差分别为194.3762和11.8219，可见7阶Gaussian金字塔压缩与实际数据更加吻合，在减小信道占用量的情况下保证了信息传输的正确性。

5.2 拉普拉斯塔式分解频谱空穴检测

在低轨卫星通信卫星频谱感知过程中由于原始信号的抖动很大，造成感知结果的误判概率增高。而拉普拉斯金字塔相当于一个高通滤波器，保留了感知信号的高频分量，也就是信号的细节部分，因此信号通过多阶的拉普拉斯金字塔变换后，频谱空穴会逼近于0，因此可以利用多分辨率频谱检测技术清晰的判断出频谱空穴的存在以及对应的频点。

为了构造拉普拉斯金字塔首先要对高斯金字塔进行扩展，将7阶的高斯金字塔进行1次扩展，再用6阶高斯金字塔与其相减，就可以得到如图6所示的拉普拉斯金字塔，随着拉普拉斯金字塔的阶数增加误差被放大，而相应频谱空穴对应的频段，其数值接近于0，设定虚警概率PF=10−5，信噪比SNR=10 dB，并取初始Δf0=10 kHz，利用多分辨率频谱检测技术对频谱空穴的数量和位置进行计算，其数量结果如图7所示。

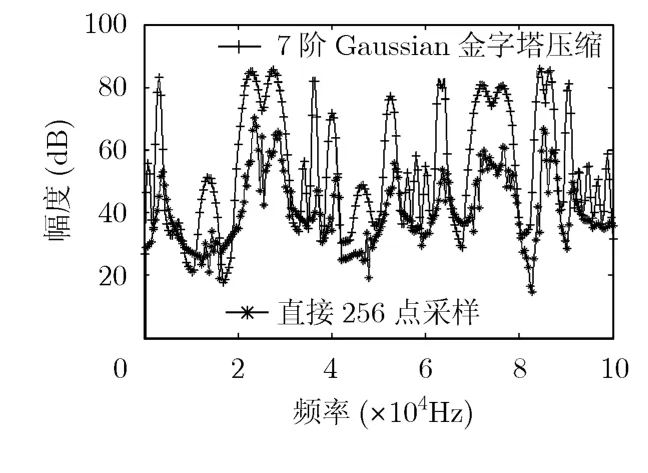
图5 7阶高斯金字塔压缩(256点)与直接256点采样比较

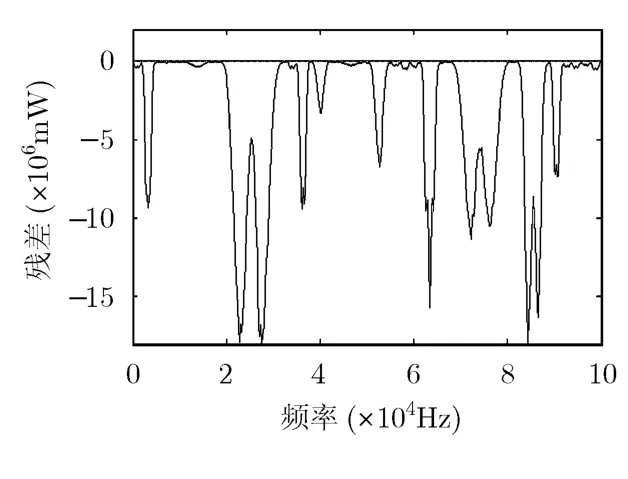
图6 作为多分辨率频谱感知 数据源的7阶拉普拉斯金字塔

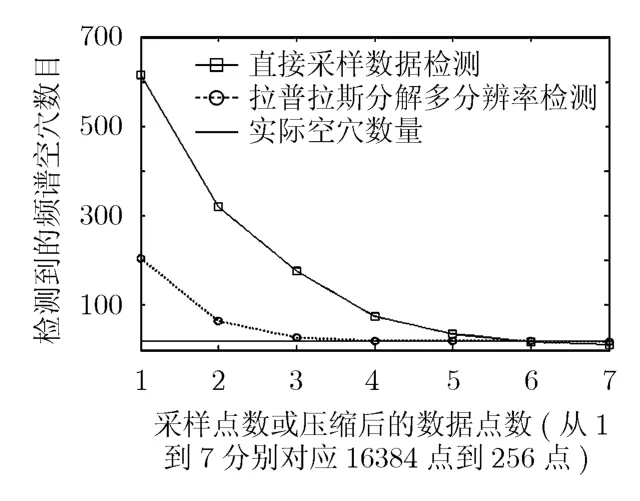
图7 直接采样频谱检测与 拉普拉斯多分辨率频谱检测比较

为了进行对比，本文统计了从16384点到256点的直接采样数据进行频谱检测，同时对从1阶到7阶的拉普拉斯金字塔分解后的数据进行频谱检测，并使用了10个时间序列求均值。如图7所示，虚线表示实际存在的频谱空穴数为20。在采样点较多的时候，由于原有采样数据有32768个采样点，其在频域的幅度抖动很大，这会使得能量检测器的误检概率增高，即便多分辨率信号分解在信号的分析和综合过程中对信号起到了平滑作用，但是在1阶变换和2阶变换中抖动一样会被误判成频谱空穴的存在。但是相比较直接采样而非压缩的数据，其偏差还是大幅减小了；在采样点较少的时候两者的结果都趋近于理论值，但是从给出的对应频段来看，由于直接采样在点数较少的时候已经无法完全表征信号的实际形状，所以给出的频段大部分是错误的，而拉普拉斯多分辨率频谱检测从4096点到256点都与实际值基本吻合，而且给出的频段始终一致，因此性能上远甚于直接采样频谱检测。

6 结论

本文提出了基于多分辨率信号分解的低轨通信卫星频谱感知技术，实现了某卫星通信系统对上行链路空穴检测的精度需求，减小了信号频域抖动带来的误差，加速了空穴定位算法的收敛过程。另外，此技术在保持原有频谱特征前提下，大幅压缩了反向链路的感知数据传输量，提高了星间链路和馈电链路的使用效率。因此，多分辨率信号分解技术可以显著地提高低轨通信卫星频谱感知的性能。

[1] Islam M H, Koh C L, and Oh S W. Spectrum survey in Singapore: occupancy measurements and analyses.CrownCom 2008, 3rd International Conference on Cognitive Radio Oriented Wireless Networks and Communications, Singapore, May, 2008: 1-7.

[2] Yucek T and Arslan H. A survey of spectrum sensing algorithms for cognitive radio applications [J]. IEEE Communications Surveys & Tutotials,. 2009, 11(1): 116-130.

[3] Notice of proposed rulemaking on facilitating opportunities for cognitive radio technologies, FCC ET Docket No. 03-108,December 2003.

[4] Murray J and Anderson J. MUOS_RRDD_SEIT_029,MUOS engineering memorandum: MUOS spectrum adaptation CONOPS. Revision XD, December 2006.

[5] Spooner C M. Multi-resolution white-space detection for cognitive radio, Military Communications Conference,MILCOM2007, IEEE, Orlando, Oct. 29-31, 2007: 1-9.

[6] Gardner W A. Statistical Spectral Analysis, Englewood Cliffs,NJ: Prentice-Hall, 1987, Chapter 4.

[7] Haykin S. Cognitive radio: Brain-empowered wireless communications[J]. IEEE Journal on Selected Areas in Communications, 2005, 23(2): 201-220.

[8] Ready M J, Downey M L, and Cobalis L J. Automatic noise floor spectrum estimation in the presence of signals.http://www. appsig.com/products/829b.htm, 2005.

[9] 余英林, 谢胜利, 蔡汉添等. 信号处理新方法导论[M]. 北京:清华大学出版社, 2004, 第3章.Yu Ying-lin, Xie Sheng-li, and Cai Han-tian, et al.. The Introduction of the New Methods in Signal Processing[M].Beijing: Tsinghua University Press, 2004, Chapter 3.

[10] Goutsias J and Heijmans H J. Nonlinear multiresolution signal decomposition schemes—Part I: Morphological pyramids. IEEE Transactions on Image Processing, 2000,9(11): 1862-1876.

[11] Burt P J and Adelson E H. The Laplacian pyramid as a compact image code. IEEE Transactions on Communications,1983,COM-31(4): 532-540.