脉冲噪声环境下的改进MUSIC谱估计方法

孙永梅，赵维，阚园园

(大连交通大学 电气信息学院，辽宁 大连 116028)＊

0 引言

谱估计是数字信号处理的十分重要研究领域，人们先后提出了各种谱估计的理论和方法，MUSIC谱估计因其具有分辨率高、稳定性好等优点，在生物医学工程、雷达、水声信号等领域得到广泛应用.MUSIC谱估计方法基本思想是直接对估计的随机过程相关矩阵进行特征分解，分别生成信号子空间和噪声子空间，利用信号子空间和噪声子空间的正交性，构造空间谱函数，从而进行谱峰搜索来估计信号频率.传统的MUSIC谱估计方法假定背景噪声满足高斯分布，并采用二阶统计量方法处理，但在地球物理、雷达、水声信号等领域中所涉及的噪声，往往不满足高斯分布且具有显著的尖峰脉冲和较厚的拖尾.因此在此种情况下高斯分布模型不再适用，α稳定分布模型却能很好的描述这类伴有显著尖峰脉冲和较厚拖尾的噪声［1－5］.α 稳定分布由于不存在二阶及二阶以上统计量，所以基于自相关矩阵特征分解的传统MUSIC谱估计方法已不再适用，需要研究适用于上述脉冲噪声环境的新的谱估计方法.本文首先介绍了α稳定分布信号的数学模型和传统的MUSIC谱估计方法，然后依据α稳定分布信号的特性，提出了两种改进的MUSIC谱估计方法.

1 α稳定分布模型

如果随机变量X具有式(1)所示的特征函数，则随机变量X服从稳定分布.

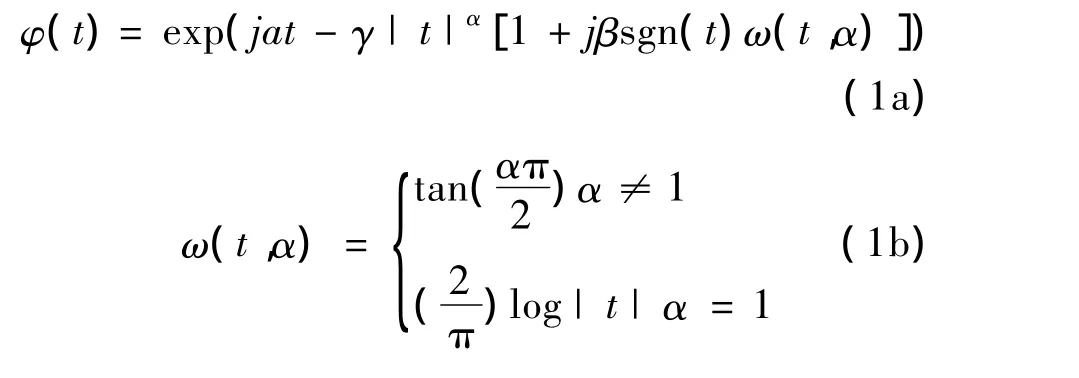
式中，sgn(·)为符号函数;α为特征指数0＜α≤2，α值越小表明分布的拖尾越厚，尖峰脉冲越显著，α=2时满足高斯分布;β为对称参数－1≤β≤1，当β=0称为对称α稳定分布(SαS);γ为分散系数γ≥0，类似高斯分布中的方差;a为位置参数，对于SαS分布当0＜α≤1时，a为中值;当1＜α≤2 时，a 为均值［2］.

2 传统的MUSIC谱估计方法

假设信号x(n)是复正弦信号加白噪声，为

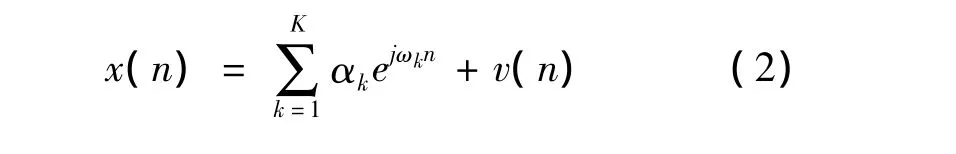
式中，αk=|αk|ejφk和ωk分别表示信号的复幅度和角频率.初始相位φk是在［0，2π］均匀分布的随机变量，并且当i≠k时，φi和φk是相互独立的;v(n)是均值为0、方差为的白噪声，且与信号相互独立.

定义信号向量

则由式(2)有

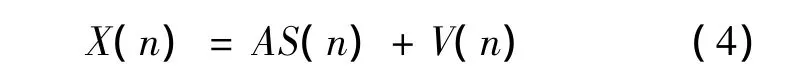
式中，

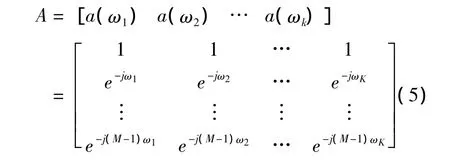
向量a(ω)、S(n)和V(n)分别定义为

向量X(n)的自相关矩阵为

式中，I是一个M×M维的单位矩阵;P是信号S(n)的自相关矩阵.

对R进行特征值分解，有

式中，US是由大特征值对应的特征向量张成的子空间，即是信号子空间，UN是由小特征值对应的特征向量张成的子空间，即是噪声子空间.在理想条件下，信号频率向量a(ωk)与噪声子空间的特征向量正交，即

由噪声子空间的向量构成矩阵

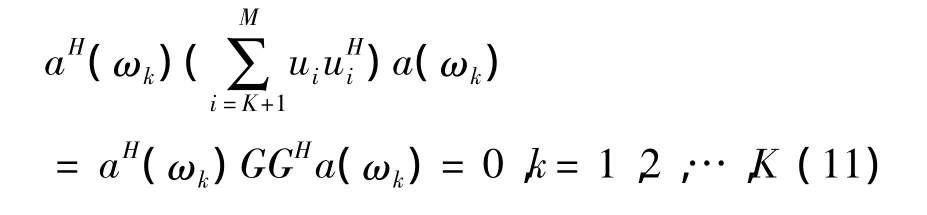
信号角频率的估计可以由函数PMUSIC(ω)的K个峰值位置确定.

谱函数PMUSIC(ω)的峰值的位置反映了信号的频率值，但是它并非信号的功率谱，一般将PMUSIC(ω)称为 MUSIC 谱［6］.

3 改进的MUSIC谱估计方法

传统MUSIC方法是通过对数据序列X(n)的自相关矩阵R进行特征分解，然后由谱函数的峰值位置搜索来进行谱估计.但是当X(n)是含有α稳定分布噪声的复正弦信号时，数据序列X(n)的自相关矩阵不存在，这种基于自相关矩阵分解的MUSIC谱估计方法在这种情况下则不再适用.

3.1 FLOC-MUSIC谱估计方法

由于α稳定分布随机变量不存在二阶及二阶以上的统计量，因此只能采用分数低阶统计量对含有α稳定分布的信号进行分析和处理.对于SαS分布随机变量X和Y，满足0＜α≤2，则X和Y的分数低阶协方差(FLOC)定义［7］为

可以看出，分数低阶协方差相当于对 x(n)和y(n)先进行非线性预处理，然后再计算互相关.

文献［8］对上述非线性处理过程进行了数学证明，结论为:如果x(n)和y(n)为μ=0的SαS分布过程，则(x(n))＜A＞和(y(n))＜A＞是满足零均值概率密度函数的对称分布，且当式(13)中的约束条件满足时具有有限的二阶矩.

本文依据α稳定分布信号的特性，利用分数低阶协方差代替MUSIC谱估计方法中的相关，可以得到一种改进的MUSIC谱估计方法(FLOC－MUSIC).下面给出FLOC－MUSIC谱估计方法步骤:

步骤1 由X(n)的N个观测样本，先对其进行如式(14)的非线性变换得到C(n)，然后构造数据序列C(n)的自相关矩阵RCC.

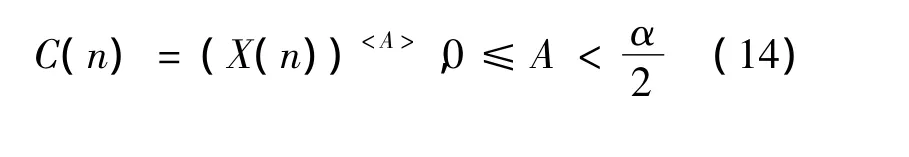
步骤2 对RCC进行特征值分解，得到M－K个最小特征值对应的特征向量，得到噪声子空间的向量，根据式(10)构造矩阵G.

步骤3 定义信号向量a(ω)=［1e－jωi…e－j(K－1)ωi］T，i=1，2，…，M，利用式(12)进行谱估计，峰值位置就是待求复正弦信号的频率.

3.2 FLOC-ROOT-MUSIC谱估计方法

对于长序列信号源，传统的MUSIC谱估计方法能很好进行频率估计，但当信号源是短序列时，传统的MUSIC谱估计方法性能退化.求根MUSIC谱估计方法将MUSIC方法转化为一种多项式求根形式，能对短序列信号源进行很好地估计［6］.

定义向量a(z)为

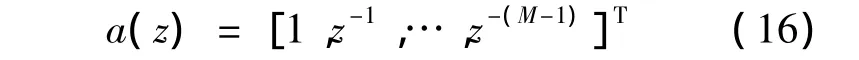
当z=ejω时，向量a(z)是频率为ω的信号频率向量.定义多项式

利用噪声子空间的向量构成矩阵G，式(17)可以表示为

由(17)可 知 zk=ejωk，k=1，…，K 是 方 程PROOT－MUSIC(z)=0的根.由于与复正弦信号频率有关的K个根zk=ejωk，k=1，…，K都位于单位圆|z|=1上，单位圆上的复数z=ejω应满足z*=z－1，所以有

将式(19)代入式(18)，得到修正方程

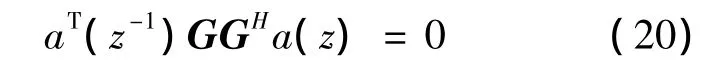
于是信号频率估计问题转化为一元高次方程求根问题，这种方法称为ROOT－MUSIC谱估计方法.

若信号源含有α稳定分布噪声，由于信号的自相关矩阵不存在，上述ROOT－MUSIC谱估计方法同样会出现退化现象.利用分数低阶协方差代替ROOT－MUSIC谱估计方法中的自相关，可以得到另一种改进的谱估计方法(FLOC－ROOTMUSIC).下面给出 FLOC－ROOT－MUSIC 谱估计方法步骤:

步骤1 由X(n)的N个观测样本，先对其进行如式(14)的非线性变换得到C(n)，然后如式(15)构造数据序列C(n)的自相关矩阵RCC.

步骤2 对RCC进行特征值分解，得到M－K个最小特征值对应的特征向量，得到噪声子空间的向量，根据式(10)构造矩阵G.

步骤3 求解式(20)，找出最接近单位圆的K个根，这些根的相位就是信号频率的估计.

4 仿真分析

设v(n)为服从α稳定分布噪声序列，信号

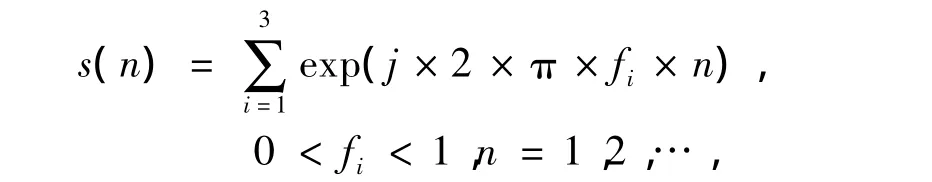
L为归一化频率.观测序列为

X(n)=A*S(n)+V(n)，其中A为M×K维矩阵，对带α稳定分布噪声的信号分别用传统MUSIC谱估计方法和本文提出的改进MUSIC谱估计方法进行频率估计，并比较三种方法的性能.信号归一化频率fi=，其中f1=0.1，f2=0.2，M=10.

4.1 高斯噪声和α稳定分布噪声环境下三种算法的性能比较

采样信号长度L=2 000，设定混合信噪比MSNR=0 dB，α分别设定为2、1.2，独立运行20次结果.仿真结果分别如图1～图3所示.

图1 传统MUSIC谱估计结果

图2 FLOC-MUSIC谱估计结果

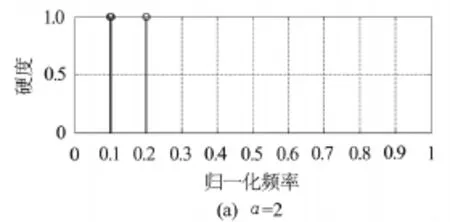
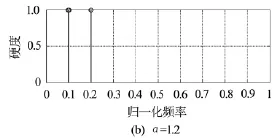
图3 FLOC-ROOT-MUSIC谱估计结果

从图1～图3中可以看出，当α=2时传统MUSIC谱估计方法、FLOC－MUSIC谱估计方法及FLOC－ROOT－MUSIC谱估计方法都能很好进行频率估计;但当α=1.2时，由于不满足高斯分布，传统MUSIC谱估计方法不再适用估计性能严重退化，而 FLOC－MUSIC谱估计方法及 FLOCROOT－MUSIC谱估计方法仍能很好进行频率估计.

4.2 不同混合信噪比下三种算法的性能比较

采样信号长度L=2000，设定α =1.2，混合信噪比MSNR 分别设定为 －10、－5、0、5 和10 dB，独立运行20次，计算每种方法的均值和标准差.仿真结果如表1所示.

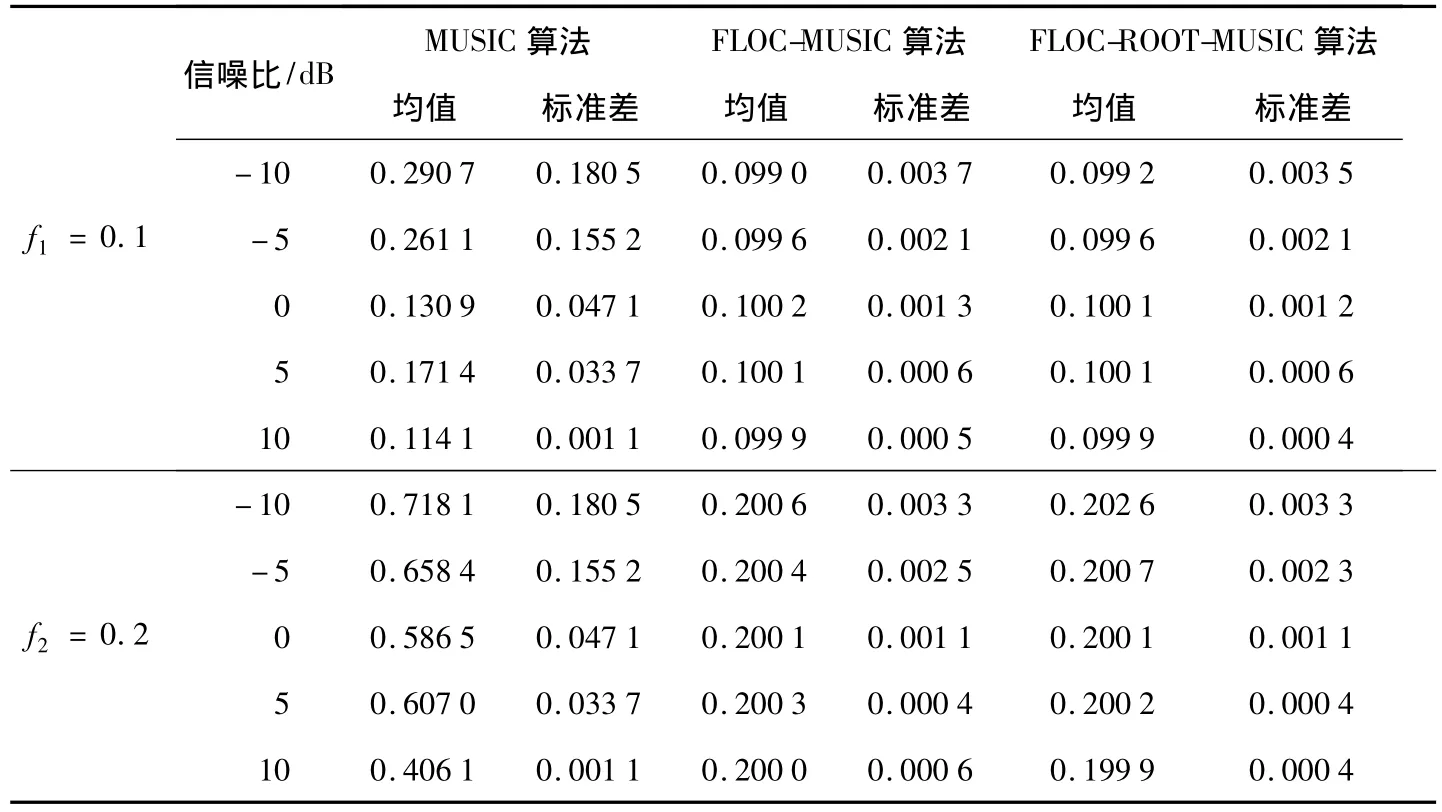
表1 不同信噪比下三种算法的均值和标准差比较

由表1可以看出，由于α=1.2，不满足高斯分布，所以基于相关矩阵分解的传统MUSIC谱估计方法的估计效果很差，而FLOC－MUSIC谱估计方法及FLOC－ROOT－MUSIC谱估计方法能对于不同混合信噪比下的带噪信号进行有效的频率估计，混合信噪比越大，估计的均值越接近于真实值.

4.3 不同α值下三种算法的性能比较

采样信号长度L=2 000，设定MSNR=0 dB，分别设定 α 为0.8、1.1、1.4、1.7、和 2，独立运行20次结果，计算每种方法的均值和标准差.仿真结果如表2所示.

由表2可以看出，当α=2时，传统MUSIC谱估计方法和FLOC－MUSIC谱估计方法及 FLOCROOT－MUSIC谱估计方法均能很好的进行频率估计.但是当α＜2时，传统MUSIC谱估计方法估计性能变差，而 FLOC－MUSIC谱估计方法及FLOC－ROOT－MUSIC谱估计方法仍能很好的进行频率估计.

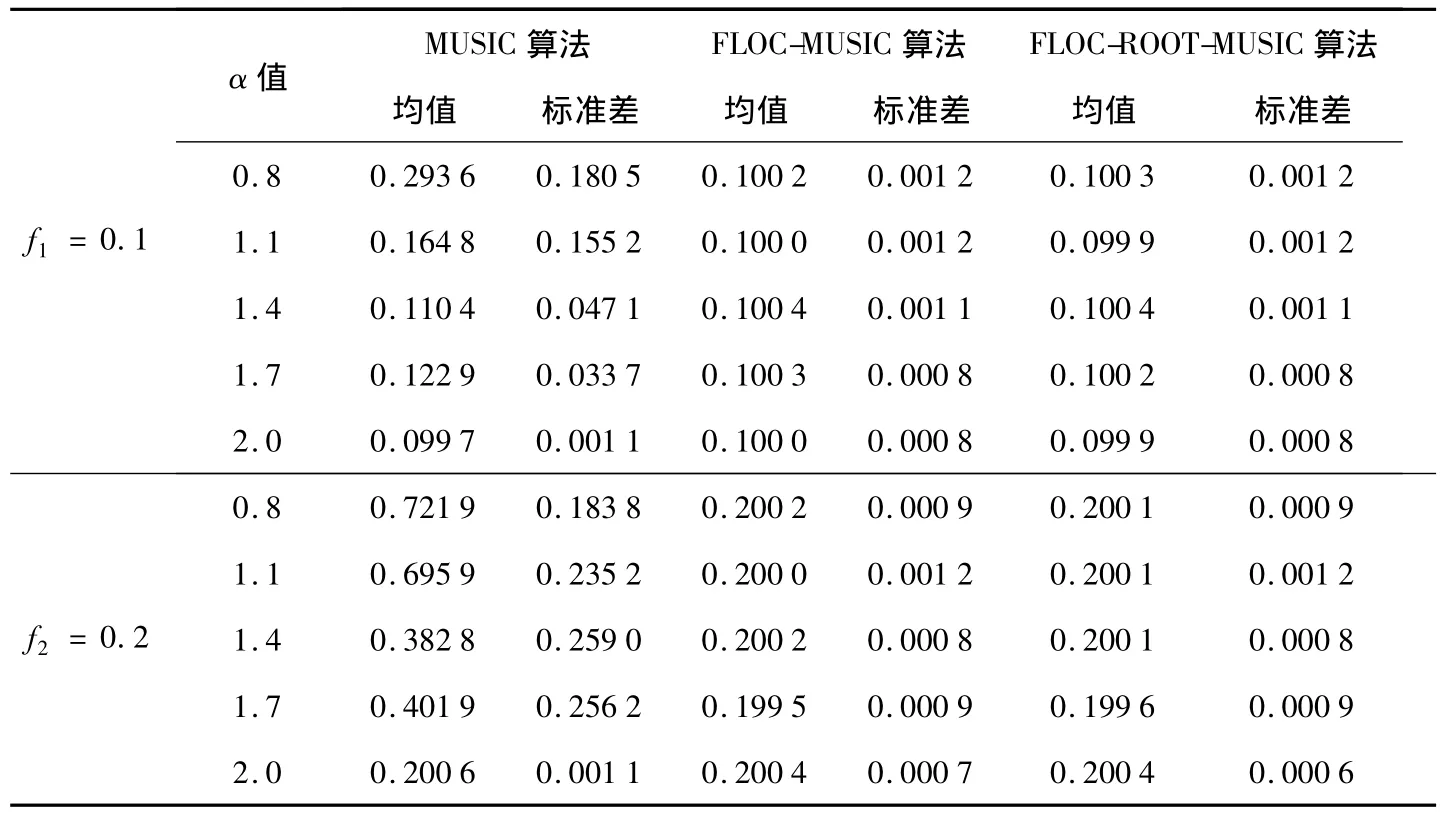
表2 不同α值时三种算法的均值和标准差比较

4.4 不同信号长度时 FLOC-MUSIC算法和FLOC-ROOT-MUSIC算法性能比较

设定MSNR=0 dB、α =1.1时，分别取采样信号长度L=2 000和L=200，采用FLOC－MUSIC谱估计方法及FLOC－ROOT－MUSIC谱估计方法进行频率估计，独立运行20次结果，计算每种方法的均值和标准差.仿真结果如表3、表4所示.

由表3、表4可以看出，对于长序列的信号源，FLOC－MUSIC 谱估计方法及 FLOC－ROOT－MUSIC谱估计方法均能很好的进行信号频率估计;对于短序列，当混合信噪比较低时，FLOC－ROOTMUSIC谱估计方法的性能明显好于FLOC－MUSIC谱估计方法.

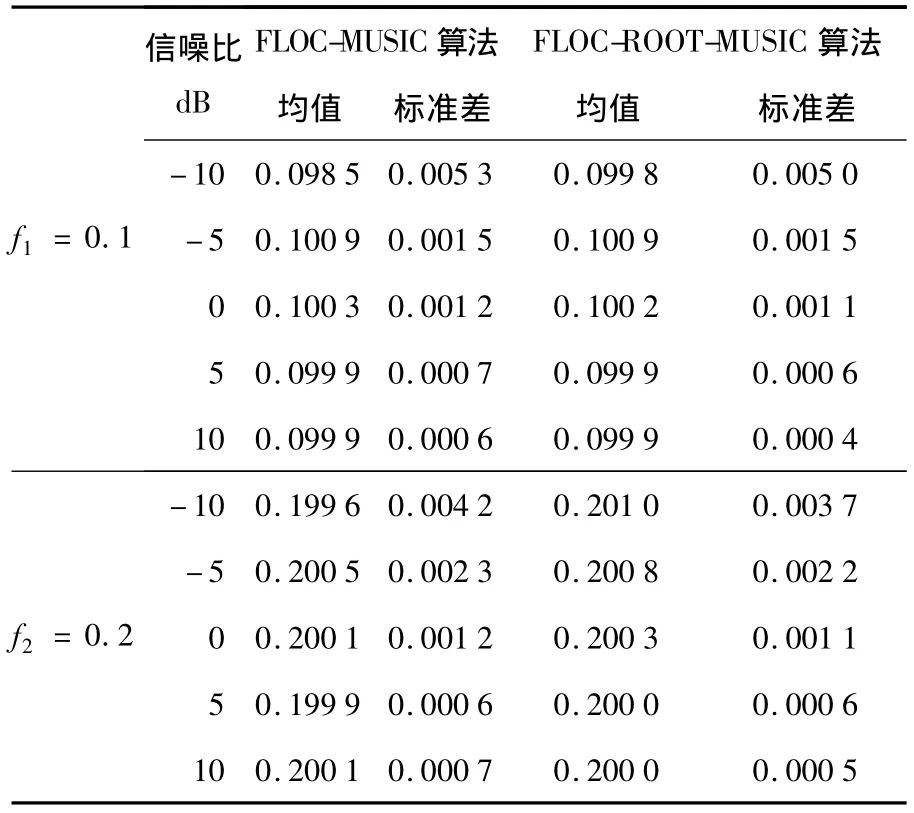
表3 α=1.1、L=2 000时不同MSNR的仿真结果

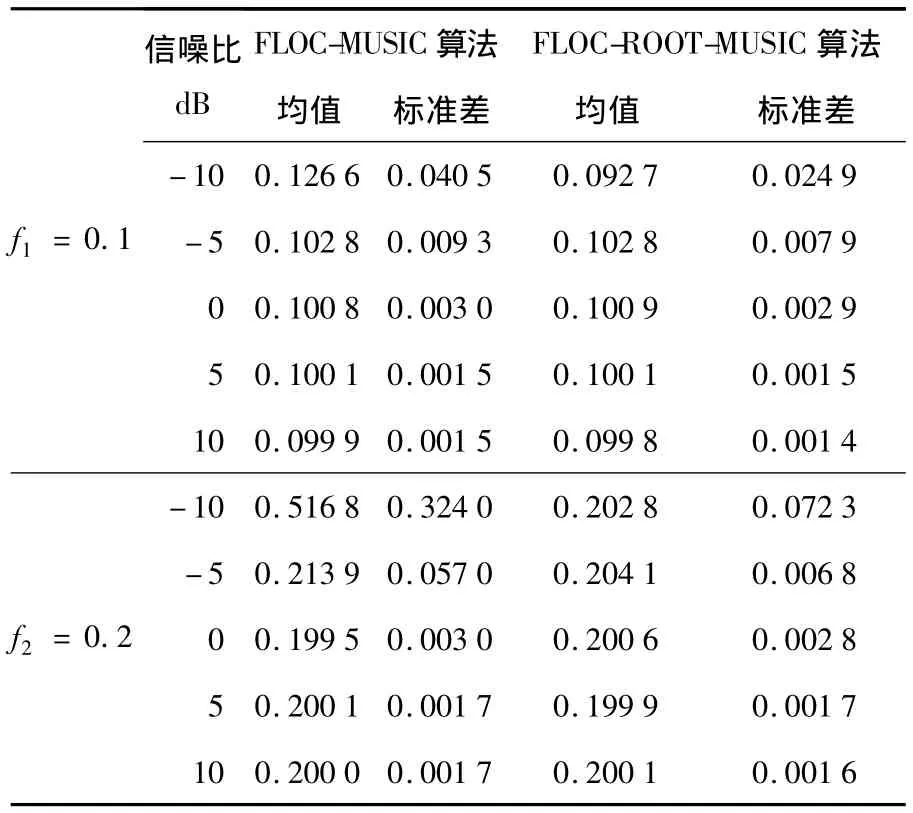
表4 α=1.1、L=200时不同MSNR的仿真结果

5 结论

由于不存在二阶统计量，所以在脉冲噪声环境下，传统MUSIC谱估计方法效果变差，本文利用分数低阶统计量的处理方法，对带噪信号进行了非线性处理，提出了改进的MUSIC谱估计方法.仿真结果表明，FLOC－MUSIC谱估计方法和FLOC－ROOT－MUSIC谱估计方法在高斯噪声和脉冲分布噪声环境下均具有良好的性能.对于带有α稳定分布噪声的短序列，当混合信噪比较低时，FLOC－ROOT－MUSIC谱估计方法的性能明显优于FLOC－MUSIC谱估计方法.

［1］NIKIAS C L，SHAO M.Signal Processing with Alpha－Stable Distribution and Applications［M］.New York:John Wiley＆Sons，Inc，1995.

［2］SHAO M，NIKIAS C L.Signal processing with fractional lower order moments:stable processes and their applications［J］.Proceedings of the IEEE，1993，81(7):987－1010.

［3］MOUNIR D，MESSAOUD B.Robust Polynomial Wigner－Ville Distribution for the analysis of polynomial phase signals in α －stable noise［J］.IEEE international conference，2004(2):613－616.

［4］MA X，NIKIAS C L.Parameter estimation and bland channel identification in impulsive signal environments［J］.IEEE Trans on signal processing，1995，43(11):2884－2897.

［5］孙永梅.稳定分布参数估计与谱分析理论及应用研究［D］.大连:大连理工大学，2006.

［6］何子述.现代数字信号处理及其应用［M］.北京:清华大学出版社，2009:110－116.

［7］MA X，NIKIAS C L.Joint estimation of time delay and frequency delay in impulsive noise Using fractional lower order statistics［J］.IEEE Transon Signal Processing，1996，44(11):2669－2687.

［8］QIU T，LI X，WANG H.An AFLC algorithm for latency change estimation of EP under alpha－stable noise condition［C］.Proce of the 25th Annual International Conference of the IEEE on Engineering in Medicine and Biology Society，Cancun，Mexico，2003:2635－2638.