物元可拓法在地铁突发事件应急能力评价中的应用

阎善郁，陈雪娇

(1.大连交通大学 土木与安全工程学院，辽宁 大连 116028;2.大连交通大学 环境与化学工程学院，辽宁大连116028)

0 引言

20世纪中期以来，城市人口规模不断扩大，地铁客流不断增加，地铁遭受突发事件的损失越来越多，因此，地铁突发事件应急变得越来越重要.而我国的应急能力建设起步比较晚，美国从20世纪40年代就开始应急预案的研究，并建立了相关的法律法规.从总体上看，国外发达国家的应急预案主要有职责法制化、职能多样化、设备现代化及专业化、指挥系统规范化、救援立体化和培训制度化等特点.这些特点使得其国家能提前研究灾害突发事件并作出预案，在灾害来临的时候能做到胸有成竹，不慌不乱，有计划，有指挥的完成灾害救助工作，能将灾害损失降到最低的程度.

目前，我国对地铁安全的认识与研究在逐步深入，地铁应急能力也在进一步提高，尤其是韩国地铁火灾、伦敦地铁爆炸发生后，人们对地铁安全正在做深层次的认识和反思，广泛研究地铁应急战略［1］.地铁突发事件应急能力评价所要解决的关键问题是，检验各级部门在应对城市地铁突发事件时所拥有的人力、组织、机构、手段和资源等应急要素的完备性、协调性以及最大程度减轻突发事件损失的综合能力［2］.基于这个问题出发，结合可拓学［3］的方法，通过物元模型，计算关联度和等级度最终得出一个定量化的结论，来了解沈阳市地铁1号线的应急能力，并以此加强地铁应急能力建设.

1 物元可拓法

1.1 经典域、节域与待评价物元

式中，Rj为第j个同征物元;Pj为地铁突发事件应急能力的第 j个等级(j=1，2，3，…，m);Ci为表示地铁突发事件应急能力的第i个评价指标(i=1，2，…，n);Vij=(aij，bij)分别为地铁突发事件应急能力等级Pj对应于评价指标Ci的量值范围，即各等级关于对应的评价指标所取的数据范围经典域.

令

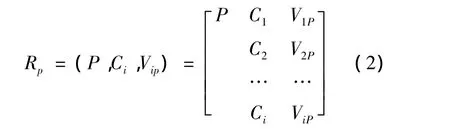
式中，P表示地铁突发事件应急能力等级的全体;V1p，V2p，…Vip分别是 P 关于 C1，C2，…Ci的取值范围，即P的节域.

对待评价的地铁突发事件应急能力P，将所收集到的数据或分析结果用物元R表示，称R为待评价物元.

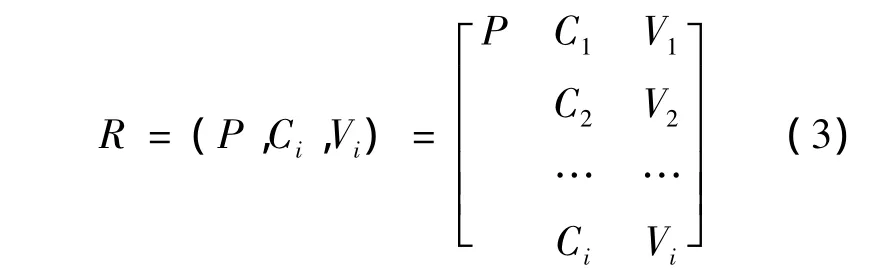
式中，P表示待评价城市可持续发展等级;Vi表示P关于Ci特征的量值，即待评城市的具体数据.

1.2 关联函数

关联函数Kj(Vi)表示被评价事物与评价标准的隶属程度的函数.关联函数的选取应当根据被评价事物的特征与可拓集合理论相结合的方法确定.针对不同的评价事物选用合适的关联函数才能更准确的反应隶属关系，对于地铁突发事件应急能力选取的关联函数为:

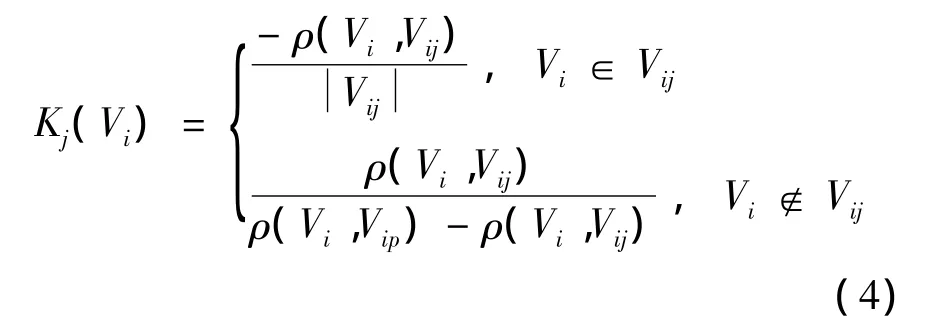
式中，

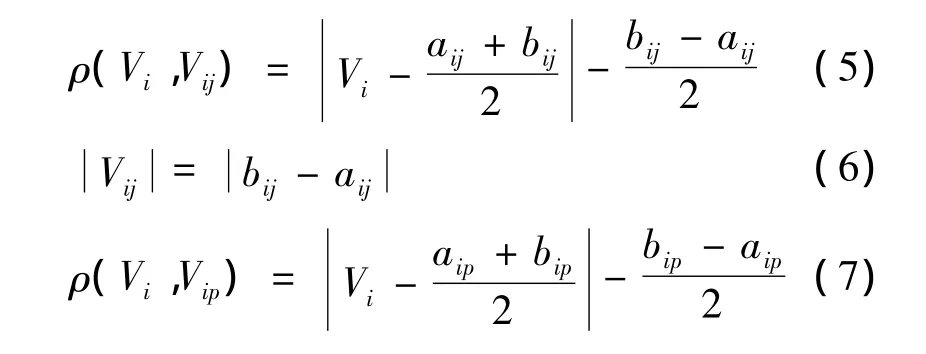
1.3 关联度与等级度

待评价地铁突发事件应急能力等级的关联度为:

综上所述，腺样体切除联合鼓膜置管能够提高分泌性中耳炎患儿的治疗效果。能够有效提高患儿的听力水平。并可降低术后并发症发生的概率，缩短术后炎性病变恢复时间，降低炎性因子的表达水平，从根本上消除腺样本肥大因素导致的复发，从而极大的降低了复发的风险。

令

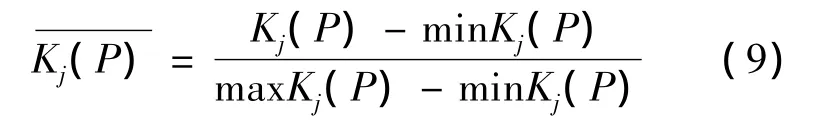
地铁突发事件应急能力的等级为:

2 应用实例

文章根据中华人民共和国中央人民政府—国家处置城市地铁事故灾难应急预案对沈阳市地铁1号线建立评价指标体系［4］，包括目标层、一级指标和二级指标.采用层次分析法［5］来确定每一个指标的权重，通过专家打分法确定的相应的指标特征值，本例经过三位专家对每一个指标按照影响因素进行打分，将每一个指标的得分平均值作为该指标的指标特征值，最后应用物元可拓法对沈阳市地铁1号线突发事故的应急能力进行评价，本例将评价结果划分为5个等级Pj=(P1，P2，P3，P4，P5)=(很强，较强，临界，脆弱，很脆弱)，计算结果见表1.

表1 地铁突发事件应急能力评价指标量化表

以二级指标预防机制为例，根据式(1)得出待评价对象的经典域为:

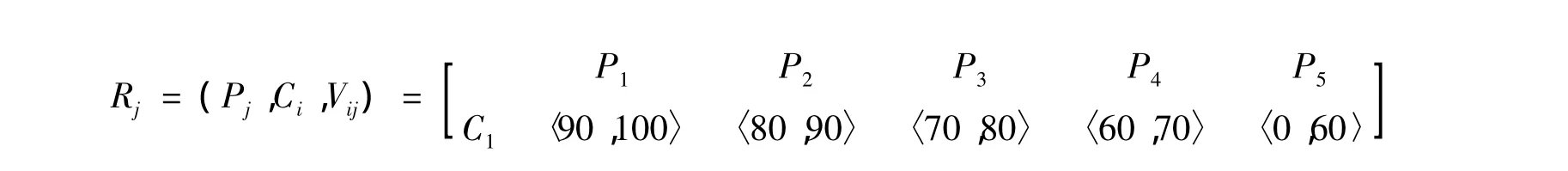
根据式(2)得出待评价对象的节域为:

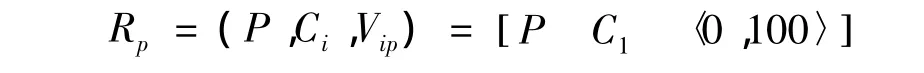
根据式(3)得到待评价物元为:

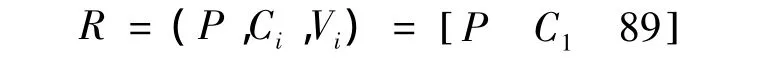
根据式(4)得出关联函数为:

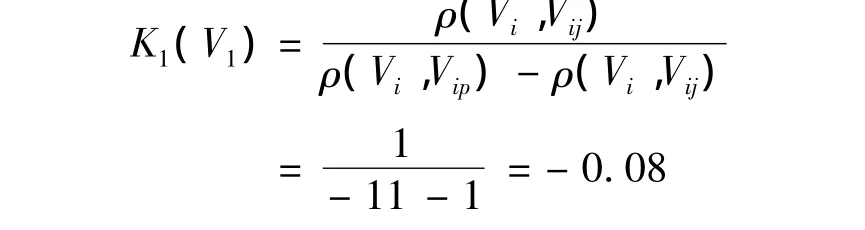
式(4)中:

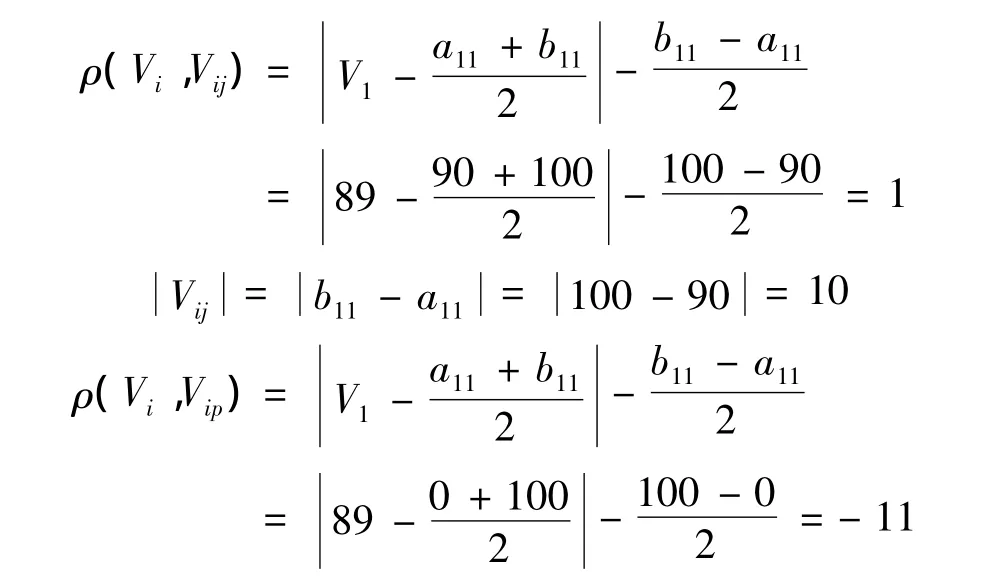
以此类推，得到其他评价指标的关联函数，再根据式(8)～(10)得出待评价对象的关联度以及评价等级计算结果为表2.

表2 关联度以及评价等级

通过表2可以得出关联度Pj=(P1，P2，P3，P4，P5)=(0.67，1，0.68，0.02，0)，最后得出的评价等级结果是2.02即沈阳地铁1号线突发事件应急能力评价结果为较强.

3 结论

(1)本文根据国家处置城市地铁事故灾难应急预案建立的评价体系比较科学合理;

(2)本文应用物元可拓法最终得出等级度来表示地铁突发事件应急能力评价结果为较强;

(3)从计算结果可以看出该方法可以用来评价地铁突发事件应急能力.

［1］王山，汪彤，代宝乾.地铁应急救援法案的研究［J］.安全，2005，26(3):23-25.

［2］黄典剑，李传贵.突发事件应急能力评价［M］.北京:冶金工业出版社，2006.

［3］李聪攀.基于可拓学的城市交通可持续发展评价研究［D］.北京:北京交通大学，2009.

［4］中华人民共和国中央人民政府.国家处置城市地铁事故灾难应急预案［EB/OL］.［2006-01-24］http://www.gov.cn/yjgl/2006-01-24/content_168999.htm.

［5］许树柏.层次分析法原理［M］.天津:天津大学出版社，1988.