稀疏阵列微波暗室成像实验研究

侯颖妮 李道京 洪 文 李南京 张麟兮

①(中国科学院电子学研究所微波成像技术国家重点实验室 北京 100190)②(中国科学院研究生院 北京 100190)③(西北工业大学无人机特种技术国防科技重点实验室 西安 710072)

1 引言

在利用阵列天线进行雷达成像的场合，为了减小雷达系统的体积和重量，通常考虑采用稀疏阵列天线代替满阵天线。稀疏阵列天线在微波辐射计[1]中获得了广泛的应用，由于采用干涉相关处理技术，要求目标信号必须互不相关，这种情况下只适用于测量目标的辐射亮温。文献[2]研究了机载雷达采用稀疏MIMO天线实现3维成像的问题，其中发射天线单元位于阵列两端，采用波形分集，形成虚拟满阵。文献[3]研究了平流层飞艇载稀疏阵列天线雷达对静止目标成像的问题，其中发射天线单元和接收天线单元位于同一位置，通过多发多收获得均匀分布的相位中心。

近年来，压缩感知理论突破了传统信号获取的概念，在实现稀疏信号重建方面，获得了迅速的发展[4,5]。稀疏重建的前提是信号本身具有稀疏特性，文献[6]利用杂波抑制后场景中运动目标具有空间稀疏的特性，对稀疏阵列接收的信号，采用基于压缩感知理论的成像算法对目标进行重建。

文献[3,6]关于稀疏阵列的研究工作主要通过计算机仿真进行了验证，对于实际工程应用，这还不够。针对此问题，本文开展了暗室实验研究工作。

2 暗室实验系统

实验系统采用收发分置的工作方式，步进频率信号由矢量网络分析仪的输出端口经功率放大器放大后发射出去，回波信号由接收天线送入矢量网络分析仪输入端口。整个数据获取采用时分工作方式，通过开关切换模拟多发多收的过程，微波暗实验系统的组成和布局如图1所示。微波暗室的尺寸为25 m(长)×15 m(高)×15 m(宽)，子阵尺寸为10 cm×7 cm。

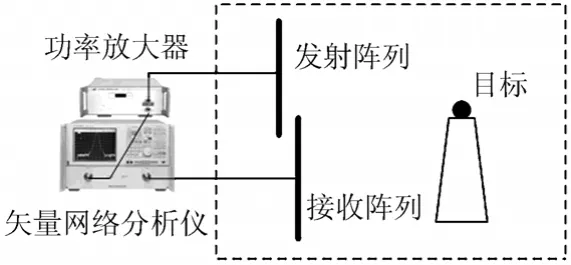
图1 实验系统组成和布局图

为了对稀疏阵列孔径综合方法[3]进行验证，同时考虑到实验系统的易实现性，采用5个子阵稀疏布置在1，2，4，6，7位置，子阵间的最小间隔为10 cm，通过多发多收可以获得均匀分布间距为5 cm的13个相位中心。由于实验采用收发分置的工作模式，因此使用2组由5个子天线组成的阵列，分别作为发射和接收阵列。实验中发射和接收阵列布置情况如图2所示，设置了4个三面角反射器作为目标，如图3所示。

图2 发射和接收阵列

图3 实验中设置的目标

3 信号处理方法

阵列天线成像雷达的主要特点之一就是多通道，各通道的幅度和相位不一致性将影响阵列天线雷达的成像性能，因此在成像处理前需要对各通道的幅度和相位误差进行校正。

3.1 幅度误差校正

对存在阵列幅度误差情况下的数据，可以在处理前用各通道接收信号的输出功率，对各通道接收的数据进行归一化，以消除通道不一致性所带来的影响。

3.2 相位误差校正

实验中发射天线和接收天线的位置偏差，以及发射天线和接收天线后的电缆长度偏差都将引起相位误差，未知的相位误差将导致方位向聚焦不准确，使得图像质量下降，严重时将导致方位向无法聚焦。

针对相位误差给出了一种简单的误差估计方法，该方法首先确定一个目标作为参考目标，根据目标和阵列的空间关系计算出理想相位历程，然后从实验数据中提取实际相位历程，最后将实际相位历程与理想相位历程之差作为系统相位误差。

当目标位于(R0, X0)时，各子阵到目标距离为

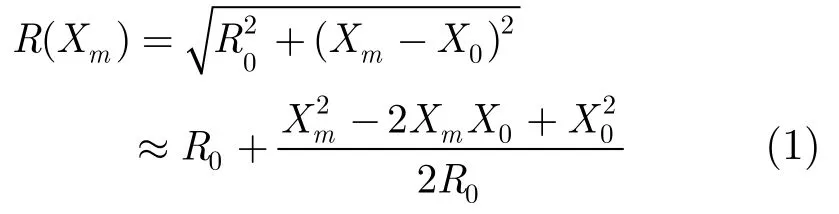
Xm为各子阵位置，由于收发双程，其相位历程为

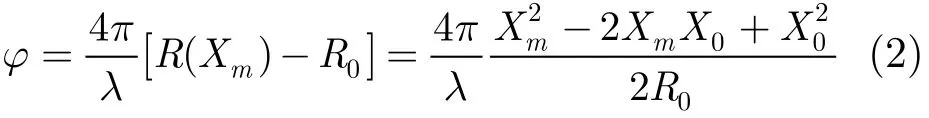
从式(2)可知，相位历程曲线二次项系数与目标到阵列的垂直距离R0有关，λ为波长，二次项系数为

对于空间参考点目标，可以提取各通道峰值点的相位值并进行解缠绕，从而得到峰值点回波的相位历程φ，系统相位误差可通过式(4)计算

应当指出的是，在提取孔径综合后各通道实际相位历程时，需要根据已知参数对各通道数据进行等效相位中心相位补偿[7]，系统相位误差可通过以下几个步骤估计：(1)根据已知参数计算出理想阵列的相位历程β；(2)根据已知参数对各相位中心处的数据进行等效相位中心相位补偿；(3)通过互相关法对各通道的采样点进行搜索，得到各通道峰值点的位置，提取各通道峰值点的相位并进行相位解缠，得到阵列误差存在条件下等效均匀阵列的相位历程φ；(4)由公式(4)计算出系统相位误差。

3.3 基于压缩感知理论的成像算法

一个维数为N的信号x可表示成xN×1=ΨN×NθN×1，Ψ为基矩阵，θ为系数矩阵。对于测量数据sM×1，sM×1=ΦM×NxN×1，由于M＜N，从sM×1恢复xN×1，是欠定方程的求解问题，如果系数矩阵θ中有K个非零元素，感知矩阵Θ=ΦΨ满足RIP，则可以从M维稀疏测量数据中，恢复出K个较大的系数，M=O(Klg(N/K))，Φ为测量矩阵。可以利用凸优化算法[8]，通过求解式(5)的ℓ1模最小优化问题，将信号x从s中恢复出来。

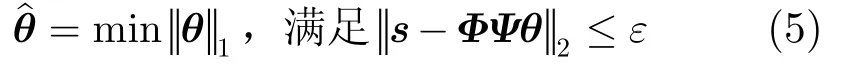
其中ε为测量数据中的噪声水平。

目标成像的过程就是目标散射系数重建的过程，基于压缩感知理论，可构造模型

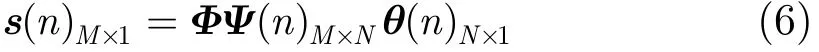
其中n为距离门数，s(n)M×1为脉冲压缩后信号的向量，θ(n)N×1为要恢复的目标散射系数向量，Φ由稀疏阵列构型决定，Ψ(n)M×N为基矩阵。

在正侧视时，接收的信号经过脉冲压缩后为[9]

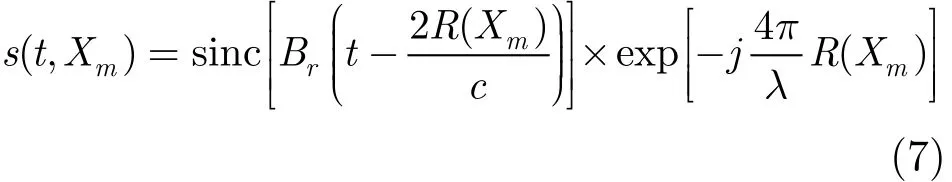
其中R(Xm)为各子阵到目标的斜距，Br为信号带宽，Xm为子阵的方位向位置，m=1,2,…,M ，M为子阵数目。

压缩感知理论中的基矩阵可根据式(7)中的指数项构造，将式(1)带入式(7)，并忽略常数相位有

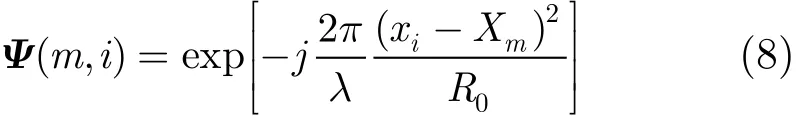
其中xi为待重建区域的方位向位置，i=1,2,…,N 。

可以看出，距离向采用传统脉冲压缩处理方式，方位向根据稀疏阵列构型和脉冲压缩后信号形式，构造基矩阵，利用压缩感知理论对目标进行重建。

4 实验数据处理

下面通过实验数据处理，对阵列误差校正方法，稀疏阵列孔径综合方法和基于压缩感知理论的成像算法的有效性进行验证。

(1)阵列误差估计 下面以孔径综合后13个相位中心数据为例，对阵列误差估计过程进行说明。

实验中发射信号的带宽为6 GHz，频率范围为12 GHz到18 GHz，考虑到三面角反射器的尺寸大于距离分辨率，影响理想点目标模型，因此可对14 GHz到16 GHz的2 GHz带宽数据进行分析，对应的距离分辨率为7.5 cm。为了确定数据的幅度和相位误差，对于获得的4个目标回波数据，可对其中一个目标的回波信号进行分析，同时为了避免其它目标的影响，首先可在高的距离分辨率条件下，在时域对所选取的目标进行距离加窗，然后再变换到频域降低带宽。

对于参考目标数据，分别计算出稀疏阵列孔径综合后1到13通道的输出功率，以最大输出功率为参考，得到各通道输出功率比如表1所示。在幅度误差校正时，对各通道接收数据分别除以表1中对应的系数，可消除各通道幅度误差。

表1 各通道输出功率比较

相位误差可以通过提取参考目标数据各通道的相位历程与均匀线列阵的相位历程之差获得，具体可以通过3.2节的4个步骤进行计算。图4为等效相位中心相位补偿后各相位中心峰值点的相位历程曲线；图5为得到的系统相位误差曲线，是由实验中与各子阵相连接的电缆长度不相等以及各子阵安装位置存在的偏差引起的。

(2)阵列误差校正前后比较 下面采用BP算法[10]对阵列误差校正前和阵列误差校正后的数据进行成像。图6为阵列误差校正前的成像结果；图7为利用估计出的幅度误差和相位误差，进行误差校正后的成像结果。表2为阵列误差校正前和阵列误差校正后图像质量指标比较。

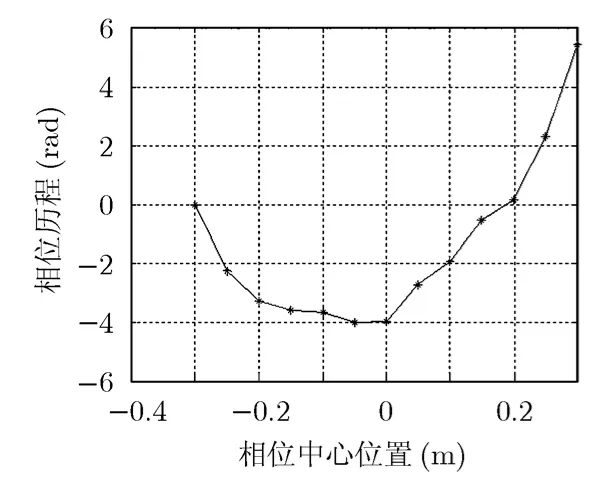
图4 由数据中得到的相位历程

图5 系统相位误差

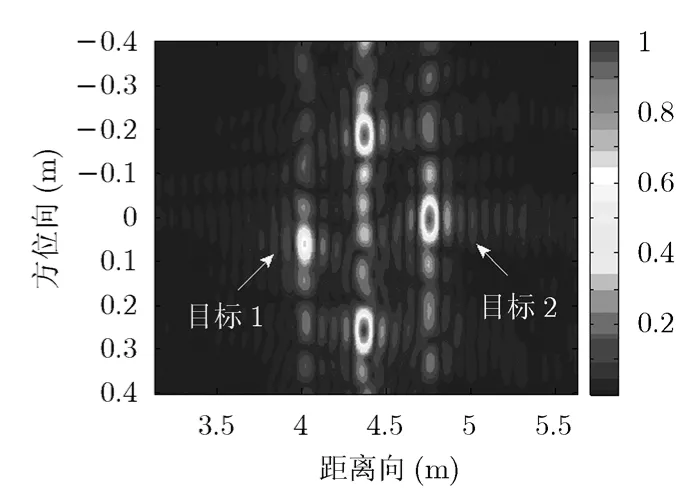
图6 阵列误差校正前成像结果

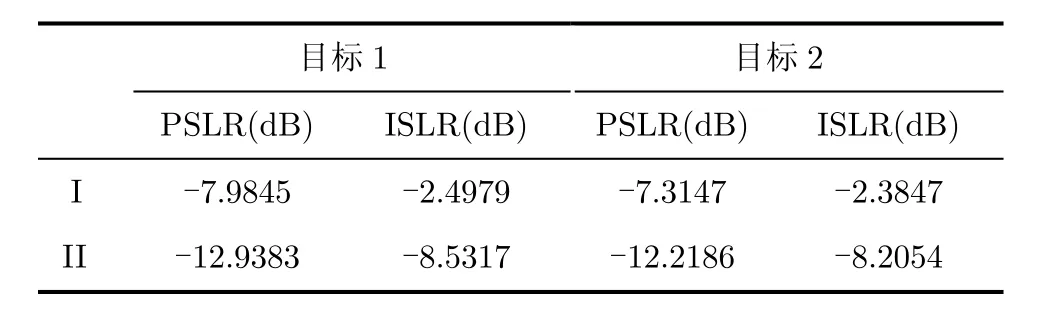
表2 图像质量指标比较

表2中Ⅰ表示阵列误差校正前，Ⅱ表示阵列误差校正后，PSLR为峰值旁瓣比，ISLR为积分旁瓣比。从图6，图7和表2的阵列误差校正前后目标峰值旁瓣比和积分旁瓣比的变化可知，经过幅度和相位误差校正后图像质量有了明显的提高，说明了阵列误差校正方法的有效性。

(3)稀疏阵列孔径综合前成像分析 下面对位于阵列中间位置的子阵发射，全阵接收的数据进行分析。此时，各相位中心间距为5 cm，与多发多收情况相同，但是等效阵列长度为多发多收时的1/2，意味着方位向不模糊范围和多发多收相同，而方位向分辨率为多发多收时的1/2。

在成像处理前，先采用3.1节和3.2节的方法对稀疏分布的5个通道进行误差估计和校正，具体过程不再详细叙述。图8为稀疏阵列孔径综合前单发多收时成像结果。

从图7和图8比较可知，采用稀疏阵列孔径综合前单发多收获得的数据进行成像，方位向旁瓣较高，而且方位向分辨率低于多发多收孔径综合后情况，进一步验证了稀疏阵列孔径综合方法的有效性。

(4)基于压缩感知理论的成像分析 下面采用微波暗室实验数据，对基于压缩感知理论的成像算法进行说明，并对采用压缩感知理论成像算和传统成像算法处理的结果进行比较。

采用单发多收获得的5个通道数据进行成像，为了保证成像效果，对分离出作为参考目标的单目标数据进行处理。在成像处理前，需要进行等效相位中心相位补偿和阵列误差校正，成像中的测量向量由稀疏阵列构型决定。图9为目标所在的距离门计算出的散射系数向量；图10为得到的成像结果，可以看出，由于距离向采用传统脉冲压缩处理方法，因此距离向旁瓣分布情况与传统处理方法的相同。

下面对多目标数据进行处理，由于单发多收5个通道数据较少，因此可以从多发多收孔径综合后的数据中抽取部分通道数据，其中采用的数据各相位中心位置之差需要同时包含奇数和偶数，这样可保证方位向不模糊区间由最小间隔5 cm决定。利用孔径综合后[5，6，7，8，10，11，12，13]共8个通道的数据进行成像比较。图11为采用基于压缩感知理论成像算法对多目标数据处理得到的成像结果；图12为采用传统BP算法对同样数据处理得到的成像结果。

从图11和图12处理结果比较可以看出，对方位向稀疏采样的数据，采用基于压缩感知理论成像算法正确恢复出了目标的方位向位置，而采用传统处理算法得到的图像方位向旁瓣较高。

5 结束语

本文利用微波暗室实验数据，对稀疏阵列孔径综合方法和基于压缩感知理论的成像算法的正确性和有效性进行了验证，针对实验中存在阵列误差给出了具体的补偿方法，并通过实验数据处理验证了阵列误差补偿方法的有效性。本文的研究工作对于稀疏阵列成像实际应用具有一定的参考价值。

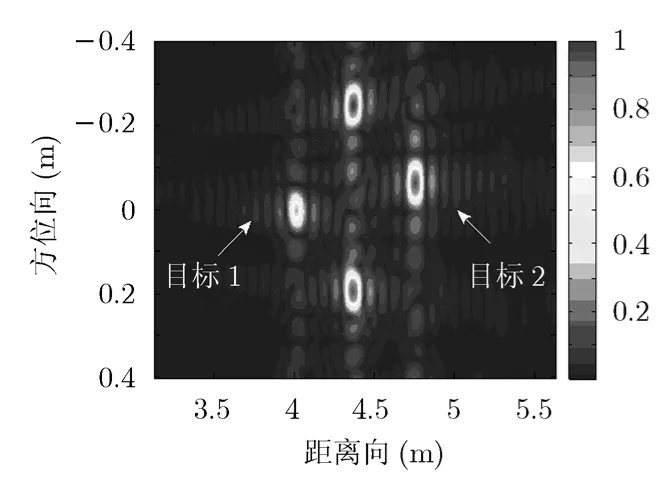
图7 阵列误差校正后成像结果

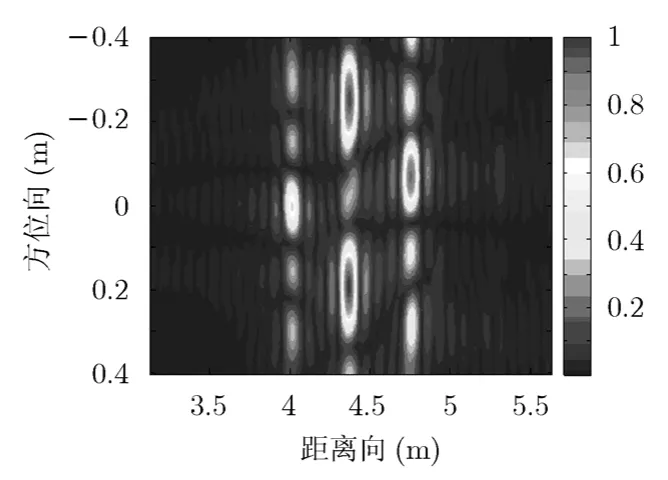
图8 稀疏阵列孔径综合前成像结果

图9 目标散射系数向量

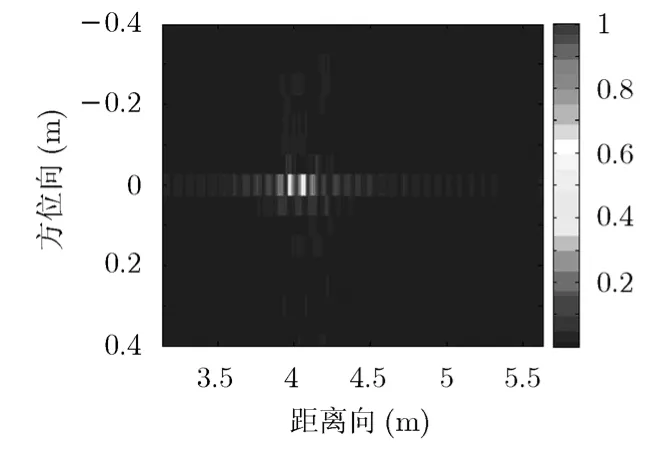
图10 单目标成像结果

图11 压缩感知理论成像结果

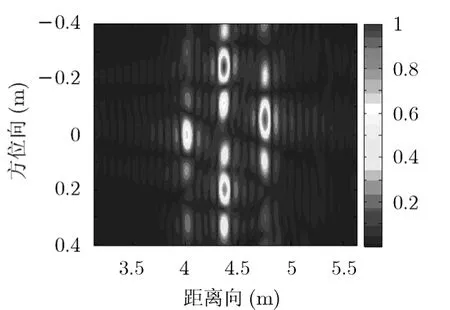
图12 BP算法成像结果

[1] Ruf C S, Swift C T, and Tanner A B. Interferometric synthetic aperture microwave radiometry for the remote sensing of the earth [J]. IEEE Transactions on Geoscience and Remote Sensing, 1988, 26(5): 597-611.

[2] Klare J. Digital beamforming for a 3D MIMO SAR-Improvements through frequency and waveform diversity[C]. IGARSS , Boston, USA, 2008: V-17-V-20.

[3] 侯颖妮, 李道京, 尹建凤等. 基于稀疏综合孔径天线的艇载成像雷达研究[J]. 电子学报, 2008, 36(12): 2377-2382.Hou Y N, Li D J, and Yin J F, et al.. Airship imaging radar based on aperture synthesis of thinned array[J]. Acta Electronic Sinica, 2008, 36(12): 2377-2382.

[4] Baraniuk R and Steeghs P. Compressive radar imaging[C].IEEE Radar Conference, Waltham, 2007: 128-133.

[5] Donoho D L. Compressed sensing [J]. IEEE Transactions on Information Theory, 2006, 52(4): 1289-1306.

[6] 侯颖妮, 李道京, 洪文. 基于稀疏阵列和压缩感知理论的艇载雷达运动目标成像研究[J]. 自然科学进展, 2009, 19(10):1110-1116.Hou Y N, Li D J, and Hong W. Airship radar moving targets imaging based on thinned array and compressed sensing theory[J]. Progress in Natural Science, 2009, 19(10):1110-1116.

[7] Li Z F, Bao Z, and Wang H Y, et al.. Performance improvement for constellation SAR using signal processing techniques. IEEE Transactions on Aerospace and Eectronic Systems, 2006, 42(2): 436-452.

[8] Grant M and Boyd S. CVX: Matlab software for disciplined convex programming. http://stanford.edu/～boyd/cvx, 2009,7.

[9] 保铮，邢孟道，王彤. 雷达成像技术 [M]. 北京: 电子工业出版社, 2005.

[10] Soumekh M. Synthetic Aperture Radar Signal Processing with MATLAB Algorithms [M]. New York: Wiley-Interscience, 1999: 212-215.