一种用哈达玛矩阵进行置乱变换的盲水印算法

林爱英， 吴莉莉， 苏 金， 郑宝周

(1.河南农业大学理学院，河南郑州 450002;2.武汉大学信息管理学院，湖北武汉 430072)

0 引 言

数字水印技术是一个崭新的研究领域，是涉及信息、信号处理、多媒体技术、计算机技术及密码学的交叉学科[1]。目前水印嵌入方法大致可分为空域方法和变换域方法2类。从综合性能对比来看，变换域方法更加优越，未来的趋势也当以变换域方法为主流。本文提出了一种基于分块离散余弦变换(discrete cosine transform，简称DCT)的变换域水印嵌入方法。该算法在水印嵌入之前首先用哈达玛矩阵对水印图像进行预处理;然后对宿主图像进行分块DCT变换，在其DCT中频系数上嵌入哈达玛矩阵置乱后的水印;最后充分利用哈达玛矩阵的正交性进行盲水印检测。实验结果表明，该算法对JPEG有损压缩和常见的图像处理有较强的鲁棒性。

1 水印预处理技术

常用的基于空间像素坐标置乱的方法有A rnold置乱和幻方置乱。本文提出了一种用Hadamard矩阵[2]对水印图像进行置乱的方法，即用Hadamard矩阵对水印图像进行相乘运算，其变换的不是水印的空间像素坐标位置，而是水印的灰度大小。2阶哈达码矩阵H2为:

4阶哈达码矩阵H4为:

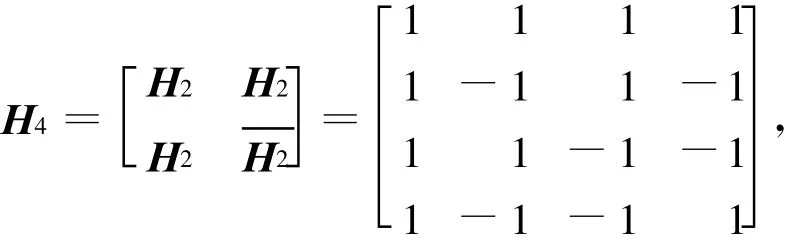
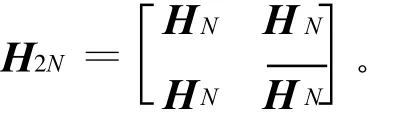
本文中采用的水印图像是大小为64×64的二值图像，Hadamard矩阵的大小也是64×64。在置换前二值(0和1)水印图像首先映射为值是1和-1的二值图像，便于Hadamard矩阵处理，置换后进行反变换恢复水印。图1为原始水印图像和用不同Hadamard矩阵对水印图像置乱后的水印图像。可以看出:采用Hadamard矩阵进行预处理之后的水印图像，即使攻击者通过某种方法获得，也无法辨认出其具体意义，因而这种预处理对水印的安全性有一定程度的提升。

图1 原始水印及其置乱后的图像

按照上述方法产生的标准Hadamard矩阵，其行列元素的排列是具有一定规律的，图1b即为采用标准Hadamard矩阵对水印进行置乱得到的水印图像。为避免攻击者得到该矩阵，可以首先对该矩阵的行列进行置换，再对水印图像进行置乱，图1c即为第1行和第64行置换、第2行和第63行置换、第3行和第62行置换……之后进行预处理得到的水印图像。可以看到不同H adam ard矩阵置乱后的水印图像有很大区别。Hadamard矩阵在水印提取时可作为密钥来使用。

2 离散余弦变换及其分块

2.1 离散余弦变换

任何连续的实对称函数的傅里叶变换中只含余弦项，DCT变换避免了傅里叶变换中的复数运算。数字图像可以看作二维矩阵，使用二维离散余弦变换对其进行分析，可用(1)式、(2)式表示[3]。

图像的DCT可以表示为:

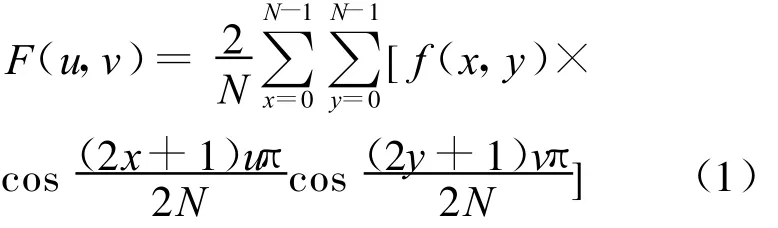
图像的离散余弦逆变换可以表示为:

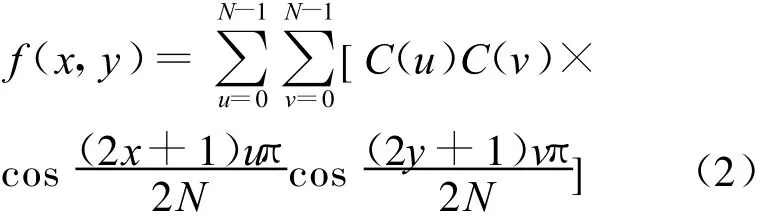
其中，x，y，u，v=0，…，N-1;C(u)、C(v)为幅度系数，且有:

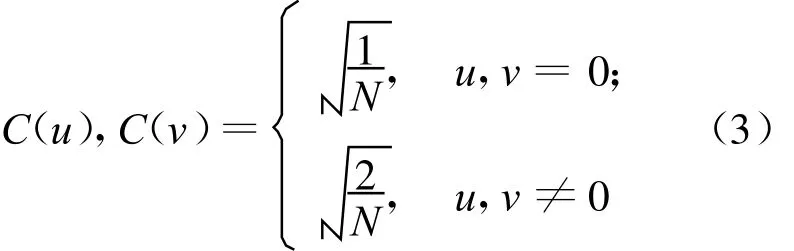
图像信号经过DCT变换后，主要能量将集中到左上角低频系数中，而右下角则包含图像更多的细节，并且变换系数几乎不相关。在变换域嵌入水印再经过反变换后，水印信号分散到各个像素中，不会造成累积误差。

2.2 图像的分块离散余弦变换

由于静止图像压缩编码JPEG是基于分块DCT变换的，所以利用分块DCT变换将水印信息嵌入到图像的频域中，是常见的嵌入方法之一。对图像进行分块是将大小为N×N的原始图像分成大小一致(设为m×m)且互不覆盖的子块，这样的子块共有将子块记为Bi，其中例如，对256×256的原图像分块，可得到32×32个8×8的子块，对每一个子块进行二维离散余弦变换都可以得到一个8×8的频域系数矩阵，这64个系数将按照0→1→2→3→4→…→63的Zigzag的顺序由低频到高频逐渐过渡。由于视觉上人眼最敏感的部分是对应于DCT变换的低频系数，所以要尽量保留低频系数。嵌入水印时通常选择频率矩阵中频系数的位置[4]，对其系数作相应的调整，频率矩阵中9→32的位置是较为合适的。

3 基于分块DCT的数字盲水印算法

3.1 水印的嵌入

原始图像记为I(x，y)(1≤x≤512，1≤y≤512)，水印图像记为J(p，q)(1≤p≤64，1≤q≤64)，原图像分块记为Bpq(m，n)(1≤m≤8，1≤n≤8)，Bpq(m，n)经DCT变换后记为Bdpq(m，n)，嵌入水印的分块记为Bdpq′(m，n)，嵌入强度记为a，提取得到的水印记为J′(p，q)。

将水印嵌入到DCT域的中频部分，选择调整Bd(4，3)、Bd(3，2)2个系数，就可得到嵌入水印的图像I′。若J(p，q)=1，使Bd(4，3)-Bd(3，2)＞a;若J(p，q)=-1，使Bd(3，2)-Bd(4，3)＞a。

该嵌入算法主要包括2部分:①J(p，q)=1时，Bd(4，3)＞Bd(3，2);J(p，q)=-1时，Bd(4，3)≤Bd(3，2);通过条件判断将水印嵌入原图的离散余弦变换系数中。②使|Bd(4，3)-Bd(3，2)|≥a，通过选择嵌入系数a保证水印的鲁棒性和不可见性。由嵌入算法可知，这里采取的是间接水印嵌入方法[5]。

另外在嵌入水印前，充分利用Hadamard矩阵正交性对水印图像进行置乱处理，可以增强水印图像的安全性。

3.2 水印的提取

上述嵌入算法提取水印时不需要原图像的参与，是一种盲水印提取算法，提取水印更加方便[6];同时可避免复杂的除法运算，直接比较DCT变换后2个中频系数的大小即可，提取过程更加准确、快捷。提取过程如下:

(1)读入待检测图像。

(2)将待检测图像按嵌入时的分块方法分成若干个互不覆盖的大小为8×8的子块。

(3)对各子块进行DCT变换。

(4)比较DCT中频的2个系数的大小，即

若Bd′(4，3)≤Bd′(3，2)，令J′(p，q)=-1;

若Bd′(4，3)＞Bd′(3，2)，令J′(p，q)=1。

(5)利用Hadamard矩阵中各行和各列的正交性，用嵌入时的H adamard矩阵对J′(p，q)进行相乘，得到提取的水印图像。

4 实验结果分析

本文采用大小为512×512、灰度级为256、类型为BMP的Lena图像作为原始图像，大小为64×64的含有“河南农大”字样的二值图像作为水印图像进行实验。用峰值信噪比(Peak Signal Noise Ratio，简称PSNR)来衡量嵌入水印后载体图像质量，用归一化互相关系数(Normalized Correlation，简称NC)来衡量提取水印与原始水印的相似性[7]。

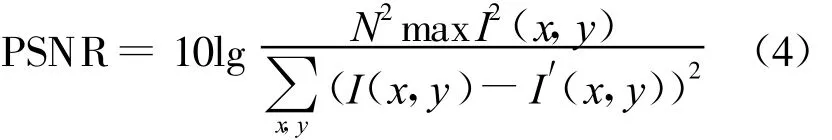
其中，I(x，y)、I′(x，y)分别表示原始图像和嵌入水印后的图像的灰度值，图像的大小是N×N;PSNR的单位是dB。

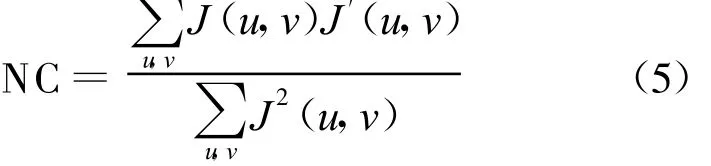
其中，J(u，v)、J′(u，v)分别表示原水印图像和提取得到的水印图像。

图2是嵌入水印之后的Lena图像及提取出的水印图像，其峰值信噪比PSNR为41.089，由此可以看出嵌入水印对原图的改变并不明显;而其NC值为1，这说明在没有攻击情况下，可以非常完好地提取嵌入的水印。图2的实验结果表明了所提出方法的可行性。

图2 嵌入水印后图像及提取的水印

对嵌入水印的Lena图像进行JPEG压缩攻击，在压缩因子为40的情况下，可以很完好地提取水印;在压缩因子为25时，提取出的水印有一定变化，但仍有效，如图3所示。

图3 JPEG压缩后嵌入水印的图像及提取的水印

对水印图像添加高斯和椒盐噪声，可以在图像改变较大的情况下提取出与原水印相似程度较高的水印，如图4所示。

图4 噪声攻击后嵌入水印的图像及提取的水印

对水印图像进行均值滤波，由于在嵌入水印时采用的是相邻系数的平均值，被攻击时均值改变较小，因此对于这类攻击具有较好的鲁棒性，如图5所示。

图5 均值滤波后嵌入水印的图像及提取的水印

表1给出了各种攻击方式下的实验结果。

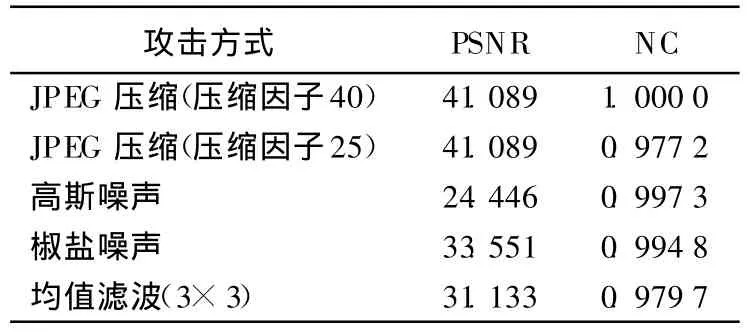
表1 各种攻击方式的实验结果

由表1可以看出，本文采用的水印嵌入策略，很好地满足了数字水印的不可见性和抗攻击性[8]，除JPEG压缩外，在高斯模糊攻击、均值滤波、添加噪声等在人类视觉系统中图像明显改变的攻击下，也展示了很好的鲁棒性。需要指出的是，本文提出的方法，其目的是改变水印各个像素的大小，相对于传统的A rnold置乱方法，即对水印图像的空间位置置乱的方法，其抗剪切性能力较差。为增强算法的抗剪切能力，可以采用H adamard矩阵置乱和A rnold置乱相结合的方法，其抗攻击能力会有显著的提高。

5 结束语

本文基于Hadamard矩阵对水印图像进行置乱的方法，把扩频通信理论应用到信息隐藏领域，将意义明确、标识性强的水印图像经过Hadamad矩阵正交置乱之后，嵌入分块DCT变换后的中频系数部分。为增强水印的安全性，首先对Hadamard矩阵进行适当的行列置换，将置换后的Hadamard矩阵作为密钥保存，以便在水印提取时使用。仿真结果证明该方法能够抵抗多种攻击，具有很好的鲁棒性，对于静态图像的版权保护具有很好的实用性。

[1] 潘 蓉.数字图像的盲水印技术研究[D].西安:西安电子科技大学计算机学院，2005.

[2] 郭梯云，邬国扬，李建东.移动通信[M].第4版.西安:西安电子科技大学出版社，2005:74-76.

[3] Gonzalez R C，Woods R E.数字图像处理[M].阮秋琦，阮宇智，译.第2版.北京:电子工业出版社，2003:378-379.

[4] Barni M，Bartolini F，Cappellini V A.DCT-domain system for robust image w atermarking[J].Signal Processing，1999，66(3):357-372.

[5] 丁 玮.基于离散余弦变换的数字水印图像[J].北方工业大学学报，1999，11(3):71-75.

[6] 曹 薇，高 隽，胡学友.一种有效的图像盲水印算法[J].合肥工业大学学报:自然科学版，2004，27(4):870-873.

[7] Dell E J.Digital w atermarking algorithm sand applications[J].Signal Processing M agazine，2001，18(4):33-46.

[8] 朱希安，郭明华.基于直流分量和低频分量的DCT域数字水印嵌入算法[J].辽宁大学学报:自然科学版，2007，34(1):20-24.