一类广义自缩序列的伪随机性
徐 林, 孙国华
(1.马钢车轮公司信息中心,安徽马鞍山 243000;2.安徽工业大学计算机学院,安徽马鞍山 243002)
0 引 言
伪随机序列在序列密码、扩频通信等领域有着极为广泛的应用。周期与相关性是衡量序列伪随机性质的一个重要而方便易行的指标。序列密码的设计准则总是高度安全性和简单结构的统一。文献[1]提出的自缩序列因结构简单而引人入胜,颇受关注[2-7],但同时因结构过于简单而使密钥的选择大受限制,并易受攻击;文献[2]给出了广义自缩序列族的概念,它们同样具有简洁的结构;并指出该序列族中每个序列的最小周期都是2n-1的因子,给出该序列族的许多密码学优点,如0~1分布的均衡性等。
1 定义及基本事实
定义1 设a=a0 a1 a2…是GF(2)上的n级m序列。设GF(2)上的n维向量G=(g0,g1,g2,,定义序列v=v0v1v2…,使vk=g0ak+对于k=0,1,2,…,如果ak=1,则输出vk,否则放弃输出。这样得到的序列b=b0 b1 b2…记为b(v)或b(G),称其为基于m序列a的广义自缩序列,称序列族B(a)={b(G),G∈GF(2)n}为基于m序列a的广义自缩序列族。
定义2 设a=a0a1a2…是GF(2)上的n级m序列,其最小周期为2n-1,极小多项式为f(x)=1+c1 x+c2 x2+…+cn-1 xn-1+xn(即序列a满足线性递归关系at=c1at-1+c2at-2+…+cn-1 at-n+1+at-n,t=n+0,n+1,n+2,…)。
以下的引理是平凡事实,参见文献[6]。
引理2 设k1,k2,…,km均为非负整数,则bi=ak1+i+ak2+i+…+akm+i,i=0,1,2,…,仍然是序列a的一个平移等价序列。
对于一个比特串P,¯P~¯P表示P的重复串,重复次数可以等于1,2,3,…,但长度必须大于0;*表示一个不定比特。
由ak-1、ak+1和ak-1+ak+1得到的广义自缩序列最小周期都是2n-1,参见文献[5,6]。文献[4]在许多情形下证明了由平移等价序列ak-2+ak-1得到的广义自缩序列最小周期是2n-1;文献[7]证明了在64种情形中有56种由平移等价序列ak-2+ak+1得到的广义自缩序列最小周期是2n-1。
本文在文献[4-9]的基础上,对被控序列Vk=ak+1+ak+2,k=0,1,2…的广义自缩序列,使用计算机编程验证,通过适当选择比特串100、1010、1101、11100、111010和111011,分析其出现次数的奇偶性,证明了该序列的最小周期在1 024种情形下全部达到最大,即2n-1。
2 序列b(ak+1+ak+2)最小周期的证明
对于周期为2的幂次的序列(如2k),如果有某个串出现奇数次,该序列的最小周期达到最大[7],即2k。从上述结论可以得知,只要证明在广义自缩序列b的2n-1长的比特串中有某个串出现奇数次,就可以得出广义自缩序列b的最小周期达到最大,即2n-1。
由引理2,ak+1+ak+2仍然是序列a的一个平移等价序列,故有广义自缩序列b(ak+1+ak+2)。
引理3 设b=b(ak+1+ak+2),则b序列中出现比特串101,当且仅当序列a中出现以下5种互不重合的情形之一:比特串101110;比特串比特串比特串比特串
证明 易知:
(1)b序列中出现比特0,当且仅当序列a中出现比特串100或111。
(2)b序列中出现比特1,当且仅当序列a中出现比特串110或者101。
综合以上事实,引理得证。
引理4 在一个周期2n-1内,序列a中形式为或且长度小于或等于n的比特串个数为偶数。
综合以上事实,引理得证。
应用与引理3或引理4的方法,可以分别得到后面的引理,故略去其证明。
由引理4得知,若当序列a的长度大于n的比特串个数为奇数时,即可以证明该序列最小周期达到最大。本文分析序列a长度大于n的比特串个数,由序列的形式可以选取cn-1、cn-2、c4、c3、c2、c1的不同值来判定序列是否满足定义2中的要求,从而推算出不同情形下满足长度大于n的比特串个数,可得到表1所列的数据。
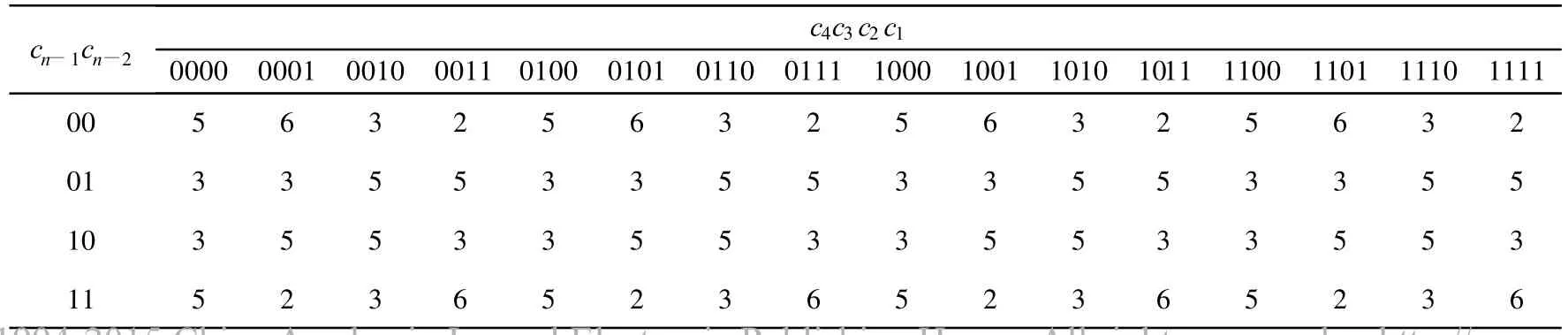
表1 b序列中存在比特串101长度大于n的相关串的出现次数
由表1可以看出,在b序列的2n-1长的比特串中,串“101”有48种情形其长度大于n的相关串出现了奇数次,但还有16种情形其长度大于n的相关串出现了偶数次,本文借助串“1011”对剩余的16种出现偶数次的情形进行讨论。
引理5 设b=b(ak+1+ak+2),则b序列中出现比特串1011,当且仅当序列a中出现以下7种互不重合的情形之一:
(1)比特串1011101。
引理6 在1个周期2n-1内,序列a中形式为或且长度小于或等于n的比特串个数为偶数。
同上,采用相同的方法分析序列a长度大于n的比特串个数,可以得到表2所列的数据。
由表2可以看出,存在36种情形其长度大于n的相关串出现了奇数次,并且在这36种情形中,有12种是在表1中不能证明周期最大情形的。也就是说,仅仅又证明了b序列最小周期达到最大时的另外12种情形,但是还有4种情形不能加以证明。
设n>13,由以上序列的形式,增加系数,选取cn-1、cn-2、cn-3、cn-4、c4、c3、c2和c1的不同值来
判定序列是否满足定义2中的要求。易得b序列中串“101”和“1011”在256种情形下未能使其周期达到最大的情形,见表3所列。
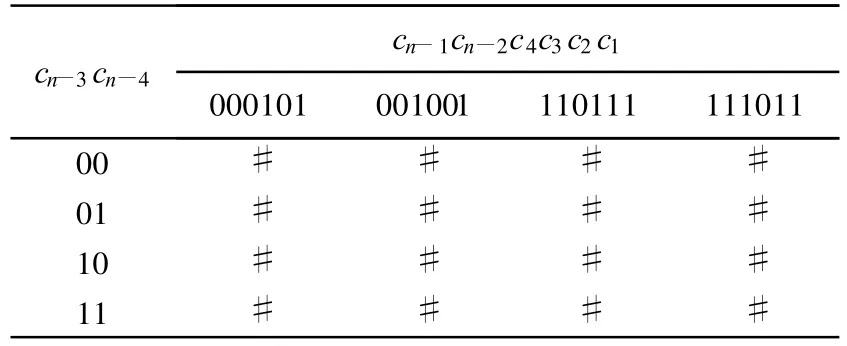
表3 b序列中未能使其周期达到最大情形
本文借助串“1101”对这16种未能说明周期达到最大的情形进行讨论。
(1)比特串1101110。
(2)比特串10101110。
引理8 在一个周期2n-1内,序列a中形式为且长度小于或等于n的比特串个数为偶数。
一是水资源供需矛盾突出。我国水资源总量位居世界第六,但人均水资源量仅为世界平均水平的1/4。经济的持续高速或较高增长,人口增长及人均消费水平的持续提高,使得供需矛盾突出,给水安全带来了日益沉重的压力,且这种压力在相当长时间内是不可逆转的。
b序列中存在比特串1101长度大于n的相关串的出现情形,见表4所列。
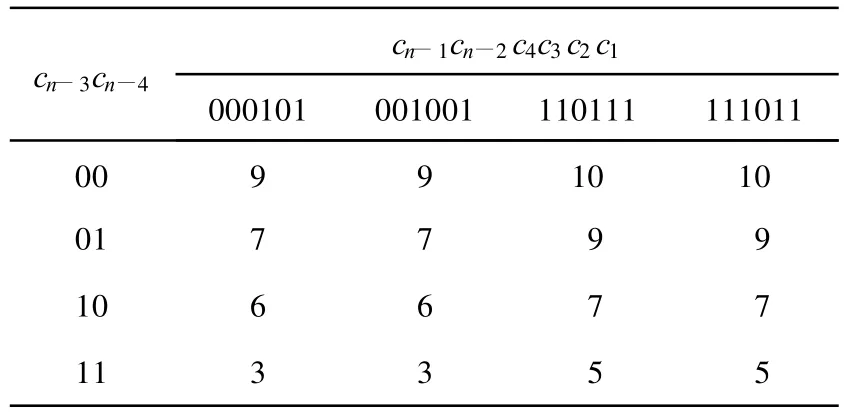
表4 b序列中存在串1101的相关串的出现情形
由表4可知,存在12种情形其长度大于n的相关串出现了奇数次,但还有4种情形其长度大于n的相关串出现了偶数次。
至此,只存在256种情形中的4种还不能加以证明,即cn-1 cn-2 cn-3 cn-4 c4 c3 c2 c1为00100101、00101001、11000111和11001011时。
采用同样的方法,相继采用比特串11100、111010和111011对序列进行分析,可以证明序列b(ak+1+ak+2)的1 024种情形在此都被证明了最小周期达到最大,此时可以得到如下定理。
定理1 广义自缩序列b(ak+1+ak+2)通过用不同的比特串101、1011、1101、11100、111010和111011来分析其出现次数,在所有1 024种情形下最小周期均达到最大,即2n-1。
3 序列b的自相关性
以下给出2个定义、1个引理及1个推论,均来自文献[7]。
定义3 如果2个串的总的相关串个数相等,且具有相同相关长度的相关串的个数相等,则它们具有相同的相关串结构。
由m序列游程分布的性质,有如下结论。
引理9 对于bjbj+k=rs,其中j的出现次数N(k,rs)分2种情形讨论,即其相关串的长度不超过n的出现次数(记为N1(k,rs)和长度大于n的出现次数(记为N2(k,rs))。
(1)相关串长度不超过n的出现次数N1(k,rs),满足:若一相关串长度为t且不含串,则它出现2n-t次;若一相关串中含有1个串并且除串外的长度为t,则它出现次;若一相关串中有b(b≥2)个串并且其除串外的长度为t,则它出现次。
(2)长度大于n的相关串的出现次数N 2(k,rs),满足:若一相关串中没有串,则它出现0次;若一相关串中有1个串并且串后边的元素数为t,则它出现t次;若一相关串中有b(b≥2)个串,除串外的长度为t,且最后一个串后的元素数为s,则它出现次。
推论 设bj bj+1…bj+k的所有相关串中,串q1 q2…ql(含有b个串)是含有串最多的一个串,则bjbj+1…bj+k的长度大于n的相关串的出现次数的上界为O(nb-1)。
引理10 序列bjbj+1=rs(其中,r和s均可以取0,1)的相关串,见表5所列。
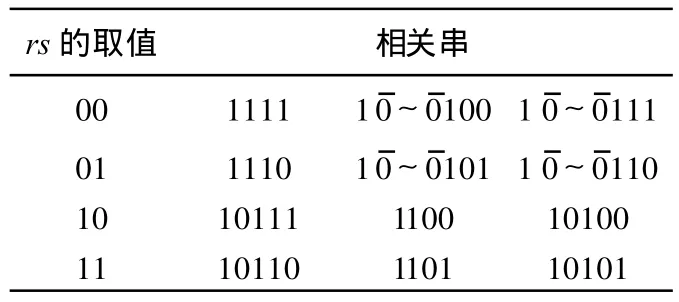
表5 bjbj+1=rs的相关串
证明 与引理3的证明完全相同。
定理2 设n≥9,则|A(1)|≤2-(n-2)。
证明 由表5可以看出,“00”与“01”和“10”与“11”具有相同的相关串结构。故由引理9,它们长度不超过n的相关串的出现次数分别相同;而它们大于n的相关串的出现次数的下界为0。设“00”与“11”的大于n的相关串的出现次数的上界分别为M1和M2,则由一阶自相关系数公式有:|A(1)|≤2-(n-1)(M1+M2),又由引理9及引理10知:M1=2,M2=0,所以|A(1)|≤2-(n-2)。
引理11 设已知bjbj+1…bj+k-1的相关串,要得到bjbj+1…bj+k的相关串:如果bj+k=0,则bjbj+1…bj+k-1的相关串末端为“11”时加“1”,末端为“01”时加“00”或“11”,末端为“10”时加“0”,末端为“00”时加“100”或“111”或或如果bj+k=1,则bjbj+1…bj+k-1的相关串末端为“11”时加“0”,末端为“01”时加“10”或“01”,末端为“10”时加“1”,末端为“00”时加“101”或“110”或“
证明 由表5可以看出,bjbj+1=rs的相关串末端有“11”、“01”、“10”和“00”这4种可能,那么由线性组合器Vk=ak+1+ak+2的结构易知结论成立。
引理12 序列bjbj+1bj+2=rst(其中,r、s和t均可以取0,1)的相关串,见表6所列。
证明 与引理3的证明完全相同。
定理3 设n≥9,则|A(2)|≤(n-1)×2-(n-2)。
证明 由表6可以看出,串“000”与“001”、“010”与“011”、“100”与“101”和“110”与“111”分别具有相同的相关串结构,所以由引理10可知,长度不超过n的相关串的个数分别相等,且长度大于n的相关串的个数的下界为0。若设比特串“000”、“011”、“100”和“110”的长度大于n的相关串的个数之和的上界为M,则|A(2)|≤2-(n-1)M,由引理9和引理12知:
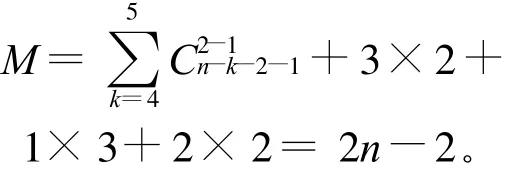

表6 bjbj+1 bj+2=rst的相关串
证明 由定义4知:
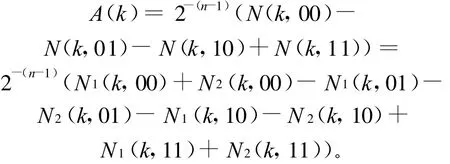
由引理10知,比特串“00”与“01”和“10”与“11”分别具有相同的相关串结构及相关串末端。由引理11知,它们分别具有相同的发展趋势;由引理9得N1(k,00)=N1(k,01)和N1(k,10)=N1(k,11),同时得到N2(k,10)与N2(k,01)的下界为0。
下面分析N2(k,00)和N2(k,11)。由引理9的推论及引理11知,只需考虑含比特串最多的且以“01”收尾的相关串,即考虑“00”与“01”的相关串,由引理12知它们随着k的每一次增长,都要增加1个串,且k=1,有1个串。那么,为k时有k个串。由引理9的推论即知,它们大于n的相关串的个数的上界为O(nk-1),也即N2(k,00)与N2(k,11)之和的上界为O(nk-1),所以2-(n-1)(N2(k,00)+N2(k,
4 结束语
本文通过采用不同的比特串分析其出现次数奇偶性的方法,证明广义自缩序列b(ak+1+ak+2)最小周期在所有1 024种情形下全部达到最大,同时证明了其具有良好的低阶自相关性。通过大量实验,发现绝大多数广义自缩序列都存在若干比特串,能说明在大多数情形下其最小周期达到最大,因而对绝大多数广义自缩序列,都可以采用选择适当的多个比特串分析其出现次数奇偶性的方法,证明其最小周期在所有情形下达到最大,即2n-1。一般广义自缩序列可以采用哪些比特串来完全证明其最小周期达到最大,还有待进一步研究。
[1] M eierW,Stafflebach O.The self-shrinking generator[C]//Advances in C ryp tology-Eurocry pt'94.Berlin:Springer-Verlag,1995:205-214.
[2] 胡予濮,肖国镇.关于m序列的自旋转序列[J].电子科学学刊,1997,19(6):847-851.
[3] Simon R B.The linear com plexity of the self-sh rinking generator[J].IEEE Trans on Inform Theory,1999,45(6):2073-2077.
[4] 胡予濮,张玉清.新一类广义自缩序列的最小周期[J].通信学报,2003,24(6):169-176.
[5] 胡予濮,肖国镇.第四类广义自缩序列的伪随机性[J].中国科学:E辑,2003,33(10):89-905.
[6] 胡予濮,张玉清,肖国镇.对称密码学[M].北京:机械工业出版社,2002:67-159.
[7] 董丽华,高军涛,胡予濮.一类广义自缩序列的伪随机性[J].西安电子科技大学学报:自然科学版,2004,31(3):394-398.
[8] Hu Yupu,XiaoGuozhen.Generalized self-sh rinking generator[J].IEEE T rans on Inform Theory,2004,50(4):714-719.
[9] 戚君贤,周建钦.一类广义自缩序列的伪随机性[J].兰州大学学报:自然科学版,2007,43(4):86-91.

