高速铣床主轴驱动透平叶栅设计与数值模拟

侯珍秀，张吉涛，陈时锦，刘金利，胡兴鸿

(哈尔滨工业大学机电工程学院，哈尔滨150001，houzx5629@hit.edu.cn)

目前，国际上高精度数控机床回转轴多采用电机驱动，最高转速为10 000～20 000 r/min［1－3］，而采用透平驱动，主轴转速可达100 000～160 000 r/min.因此，透平式气马达作为超高速主轴的驱动装置正在被广泛研究和应用.摆角铣头作为数控铣头的一种，是用于制造小型精密复杂零件的高精密数控铣床的关键部件，其研制的难点在于主轴转速极高，往往在150 000 r/min以上.

本文针对驱动其主轴的透平式气马达叶栅的造型设计和数值模拟进行了研究，对叶片进行变参数设计，得到了不同参数对其气动性能的影响规律，并获得了使叶栅气动性能最佳的参数组合.

1 平面叶栅的造型设计

摆角铣头技术要求为:转速160 000 r/min，刀头切削力矩小于0.005 N·m，气马达喷嘴数为3，压力气体初始压强 p0=0.5 MPa，环境压强p1=0.1 MPa，环境温度T=293 K.

文中采用直接绘制叶背和叶盆型线造型法来进行平面叶栅造型.设计时，假设气体在叶片流道中的流动是轴对称的，流动过程为绝热状态，且假定流动是定常的.

1.1 平面叶栅的气动力计算

1.1.1 进出口速度计算

叶片气动力计算是针对平面叶栅进行的，即将环形叶栅展布在一平面上得到的模型，其结构与速度三角形如图1所示.

图1 平面叶栅与速度三角形示意图

图1中u是叶片作周向运动的圆周速度，c1和c2是叶栅进、出口气流的绝对速度，其方向角用α1和α2表示，w1和w2是叶栅进、出口气流相对于旋转叶片的速度，其方向角用β1和β2表示和分别是α2和β2的补角.

根据摆角铣头的实际结构，取叶片中径d= 44.5 mm，叶轮以n=160 000 r/min的转速旋转，则叶片中径d处的圆周速度:

喷嘴出口气体等熵速度:

式中:k为绝热系数，对于空气，k取1.40;R为气体常数，对于空气，R取287.04 J/(kg·K).

定义喷嘴速度系数φ:

φ的数值主要取决于喷嘴的形状和加工情况，一般在0.95～0.98.由于本设计喷嘴尺寸很小，故取下限值，则喷嘴出口气流实际速度

通常情况下，在动力涡轮设计中，叶栅进气角α1值在22°～25°［4］，由于本设计转速较高，取α1= 20°～25°进行计算.以进气角α1=20°为例，对平面叶栅进行速度矢量计算，由进口速度三角形可求得β1=72.60°，w1=160.5 m/s.取β－2=69°，可得出口速度三角形(如图2所示)，进而求得出气口绝对速度c2=348.6 m/s，方向角α2=24.10°.

图2 α1=20°时速度矢量图

1.1.2 流量计算

根据动量矩定律可知，作用于物体上的外力对于某转动轴的力矩等于物体对于该轴动量矩的变化率，即

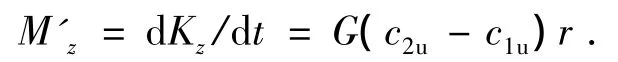
式中:M'z为作用于气流上的力对于转动轴z的力矩(N·m);Kz为外力对于z轴的动量矩(kg·m2/s); G为气体流量(kg/s);c1u为速度c1的轴向分速度(m/s);c2u为速度c2的轴向分速度(m/s).

根据牛顿第三定律，气体推动叶片的作用力在数值上等于叶片对气体的反作用力，则有

Mz为所设计的切削力矩与主轴摩擦阻力矩之和，通过计算可知主轴摩擦阻力矩与所设计的切削力矩相比很小，故计算中取Mz=0.005 N·m，当进气角α1=20°时，理论上需要的气体流量为

1.1.3 叶片高度计算

通常情况下，透平式气马达为部分进气，即喷嘴不是均布在整个圆周上，而只存在于特定的弧段.此时，叶片高度l由下式确定:

式中:e为部分进气率，取3/40=0.075;μ为流量系数，取1.0;ρ2s为出口等熵密度，取1.38 kg/m3.

将α1=20°时各项参数代入式(1)，得l= 2.9 mm，α1=25°时，l=3.5 mm.

1.2 气马达的叶型设计

采用直接绘制叶背和叶盆型线造型法［5－7］对气马达叶型进行设计，则叶型、叶栅几何参数如图3所示.取几何入口角β1g=β1(β1由速度三角形求得，值为72.6°);几何出口角(对于冲动式叶栅，即69°);安装角γ= (β1+β2)/2，即91.17°;叶栅宽度B=5 mm;弦长b=Bsin γ;叶片数z=40;进口圆半径r1= 0.3 mm;出口圆半径r2=0.6 mm.

图3 叶型、叶栅几何参数示意图

根据以上结构参数绘制的平面叶栅型线如图4.

图4 α1=20°，z=40的平面叶栅型线

2 叶栅气动特性数值模拟

2.1 有限元模型的建立

本节依次对不同进气角(叶片几何入口角)、叶片数(栅距)和叶片高度参数组合的叶栅气动性能进行数值模拟.从中找出上述各参数变化时对摆角铣头性能的影响规律.

图5和图6分别是流道区域的实体模型和有限体积模型.

图5 流道区域实体模型

图6 流道区域的有限体积模型

计算时采用三维双精度耦合隐式求解器，Realizable κ－ε双方程模型.工作介质为空气，动力粘性为1.85×10－5Pa·s.

边界条件:入口边界类型选择压力进口，马赫数Ma=1.29，总压pt=273 400 Pa，静压ps=100 000 Pa，出口边界类型选择压力远场，根据实际情况，文中出流静压为100 000 Pa，温度为297 K，出流方向矢量为(0，0，1)［8－10］.

为了检验数值模拟的正确性，首先对气流进气角α1=20°(几何进气角β1g=72.60°)，叶片数z= 40，叶片高度l=3.5 mm，叶片顶部间隙δ=0.2 mm的参数组合情况进行模拟.查看FLUENT报告得知其进口流量为2.064×10－3kg/s，与上文理论计算结果仅差1.12×10－4kg/s，即5.15%，这说明本文所建立的FLUENT模型是正确的.

2.2 进气角特性

叶栅的进气角对叶栅的流通能力、叶片表面气体压力的分布和附面层损失有重要影响.一般而言，随着叶栅的进气角增大，叶栅的流通能力增强，流量增加，但损失也会随之增大;叶栅进气角的变化势必影响叶片表面压力的分布，从而影响扩压区的位置和作用情况;叶栅的进气角还会影响附面层的生成和分离，影响附面层的厚度，从而对叶片表面的附面层损失产生影响.

图7是叶栅进气角为 α1=20°、21°、22°、23°，而其他参数固定时(z=40，l=3.5 mm，δ= 0.2 mm)，获得的叶栅气动性能数值模拟云图.α1=20°时吸力面入口段存在一个明显的扩压区，损失较大;α1=23°时吸力面入口段也存在较大的扩压区，出口段扩压区明显前移，由此产生的损失也较大.相比较而言，α1=21°和α1=22°时吸力面压力曲线分布较合理，入口段未出现明显的扩压区.

图7 不同进气角情况下吸力面总压的模拟云图

图8是叶栅流道中面上的流线轨迹图，从图中可以看出，随着进气角的增加，叶片吸力面上的附面层先变薄而后增厚;而压力面上的附面层则逐渐变厚，损失逐渐增加.对比α1=20°至α1= 23°流线轨迹图可知，α1=21°时附面层引起的损失(粘性损失)最小.

根据FLUENT报告，不同进气角情况下叶栅流道区域的流量、对旋转轴的合力矩和比功的变化情况如表1所示.

由表1可以看出，随着进气角的增大，叶栅的流量逐渐缓慢增大，而对旋转轴的力矩和比功则先增大而后下降，在α1=21°时出现最大值.

图8 不同进气角情况下流道区域中面流线图

表1 不同进气角情况下叶栅气动参数

综上，在其他参数固定情况下，进气角α1= 21°时的叶栅气动性能最佳，因此在本文以下的分析中，取α1=21°.

2.3 变叶片数特性

叶片数的改变会带来叶栅相对栅距(叶片稠度)的改变，过小的相对栅距会产生较大的摩擦损失和激波损失;过大的相对栅距会使压力面和吸力面的压力差增大.叶型表面上的最低压力随着相对栅距的增大而降低，吸力面上的最低压力点会逆气流方向移动，引起扩压区增大，从而加大了流动损失;此外，附面层也随着叶片相对栅距的增大而增厚，甚至发生分离，产生涡流损失.本文根据文献介绍的最佳栅距区间，分别取其最大值、中值和最小值，对应的叶片数分别为32、36、40.

取上文分析得出的最佳进气角α1=21°，固定其他参数(l=3.5 mm，δ=0.2 mm)，研究叶片数(相对栅距)对叶片表面压力分布以及叶栅气动性能的影响并选择最佳叶片数目.

不同叶片数情况下吸力面压力等值线如图9所示:z=32情况下的叶片吸力面压力分布最为合理，入口段基本不存在扩压区，出口段扩压区位置比较靠后，从而由扩压区的作用引起的损失也较小;z=36情况下的叶片入口段吸力面扩压区较大，但出口段基本不存在扩压区;而z=40情况下的叶片在入口段存在一个较严重的扩压区，出口段的扩压区也较大，故损失也是三者中最高的.

图9 不同叶片数情况下吸力面总压

根据FLUENT报告结果，不同叶片数情况下叶栅流道区域的流量、对旋转轴的力矩和比功的变化情况如表2所示.

表2 不同叶片数情况下叶栅气动参数

由表2可知:虽然z=32时叶栅对旋转轴的力矩最大，但因为其栅距较大，因而叶栅通道流量也较大，比功反而是最小的;z=36时叶栅对旋转轴的力矩和z=32时相差不大，但流量却比z=32时小很多，因而其比功最大;z=40时的叶栅的损失较大.

综上所述，在其他参数固定情况下，叶片数z=36时叶栅的气动性能最佳.本文以下的分析中皆取z=36.

2.4 变叶高特性

通常情况下，气体经过叶栅流道时，在叶片端部会产生自叶片压力面向吸力面的横向流动，即二次流，端部附近的主流里也会有一部分气流由吸力面向压力面流动以补偿气体的横向流动，这就会造成气道上下端壁附近两个方向相反的旋涡区，从而产生可观的能量损失.叶片高度对上述的损失具有决定性影响.对α1=21°，z=36，δ= 0.20 mm时不同叶高(l=3～4 mm)情况下叶栅的气动性能进行数值模拟.

图10是不同叶高情况下轮毂面上的流线图，从图中可以看出，虽然轮毂面未出现横向流动，但吸力面附近出现旋涡，随着叶片高度的增大，附面层厚度逐渐变薄，旋涡也逐渐变小甚至消失，因此流动损失也逐渐减小;但随着叶片高度继续增大，叶片高度方向压力梯度变大，又会使轮毂面和吸力面交汇的地方重新产生旋涡，从而使流动损失增加.

图10 不同叶高情况下轮毂面流线图

根据FLUENT报告结果，不同叶高情况下叶栅流道区域的流量、对旋转轴的力矩和比功的变化情况如表3所示.

表3 不同叶高情况下叶栅气动参数

由表3可知:随着叶片高度增大，叶栅对轴的旋转力矩和通过叶栅流道的气体流量也随之增大，并且当l=3.50 mm时，叶栅的比功最高.

综上所述，在其他参数固定的情况下，叶片高度l=3.50 mm时，叶栅的气动性能最佳.

3 结论

1)设计的叶栅气动性能良好，所建的模型经数值模拟得出的叶栅流道流量和理论计算的结果基本吻合，二者相差很小，为5.15%.

2)随着进气角的增大(从20°到25°)，叶栅的流量缓慢增大，而对旋转轴的力矩和比功则先增大而后下降.

3)在最佳栅距范围内，叶片数可选32、36和40.叶片数越少，其吸力面上压力曲线分布越合理，叶栅对旋转轴的力矩也越大，但因其栅距较大，通道流量较大，比功反而较小;叶片数过多则存在严重的扩压区，损失较大.

4)随着叶片高度的增大，附面层厚度逐渐变薄，吸力面附近的漩涡也逐渐变小甚至消失，但随着叶片高度继续增大，叶片高度方向压力梯度变大，又会使轮毂面和吸力面交汇的地方重新产生旋涡，从而使流动损失增加.

5)在进气角α1=21°，叶片数z=36，叶片高度l=3.5 mm时，叶栅的气动性能最佳.

［1］常全富.IMTS 2006展会和美国机床企业考察报告［J］.制造技术与机床，2007(1):15－18.

［2］丁雪生.CIMT2007海外展品精品介绍［J］.世界制造技术与装备市场，2007(1):48－54.

［3］丁雪生.CIMT2007参观引导和重点展品介绍［J］.制造技术与机床，2007(3):14－20.

［4］钟芳源.燃气轮机设计基础［M］.北京:机械工业出版社，1987.

［5］DUNHAM L J.A parametric method of turbine blade profile design［J］.ASME Paper，1974，74－GT－119.

［6］KORKIANITIS T.A parametric method for direct gasturbine-blade design［J］.AIAA Paper，1987，87－2171.

［7］ROBBINS W H，DUGAN J F.Prediction of off-design performance of multistage compressors［R］.［S.l.］: NASA，1965:SP－36.

［8］JOHNSON M S.One-dimensional，stage-by-stage，axial compressor performance modal［J］.ASME Paper，1991，91－GT－192.

［9］GUMMER V，GOLLER M，SWOBODA M.Numerical investigation of endwall boundary layer removal on highly-loaded axial compressor cascades［C］//ASME Turbo Expo 2005-Gas Turbie Technology:Focus for the Future.New York:American Society of Mechanical Engineers，2005.

［10］KICHEOL P.Numerical study on the effects of blade leading edge shape to the performance of supersonic rotor［C］//2003 ASME Turbo Expo.New York:American Society of Mechanical Engineers，2003.