不确定性线性系统的H∞输出反馈鲁棒重复控制

苏宝库，赵 富，2，刘 雨

(1.哈尔滨工业大学空间控制与惯性技术研究中心，哈尔滨150001，zhaofu9274@163.com; 2.北京航天控制仪器研究所，北京100854)

在许多工业应用中(如机器手、数字控制机床和转台等)，参考信号或扰动信号经常是周期已知的周期性信号，并且这些实际应用要求伺服系统具有很高的定位精度和低速性能.文献［1］基于内模原理提出了重复控制，在稳定的闭环系统内设置一个产生与参考信号或扰动信号同周期的内部模型，使得系统实现对周期性参考信号的渐近跟踪或对周期性扰动信号的有效抑制.自从重复控制提出以来，许多学者对此展开了广泛深入的研究，并且获得了成功的应用［2－5］.Hara和Yamamoto给出重复控制系统的稳定性条件［6］.文献［7］将有限维重复控制器应用于抑制转台控制系统的力矩扰动，但是要求被控对象无虚轴上的零点，没有考虑系统存在不确定性的情况.由于H∞控制理论适合处理存在数据摄动和外界扰动时系统的鲁棒控制问题，因此一些学者已经将H∞控制应用于分析和设计重复控制系统.Guvenc用1和－1分别代替内模中的时滞e－τs，利用结构奇异值理论分析连续重复控制系统鲁棒稳定性和跟踪性能，将原来无限维的问题简化成一个有限维问题.但是用此方法设计镇定控制器存在很大的保守性［8］.文献［9］在频域空间中研究了鲁棒重复控制器的设计问题，但是所提出的设计方法只能适用于最小相位系统.文献［10］在给定系统镇定控制器的基础上，基于LMI约束条件提出设计重复控制器的方法.在文献［10］的基础上，吴敏等人在保证控制系统稳定性的基础上提出了低通滤波器和状态反馈控制器参数同时优化的方法［11］.但是没有考虑扰动对控制系统的影响.

基于以上文献存在的缺点，本文针对不确定性线性系统提出一种重复控制器和输出反馈控制器参数同时优化的方法，有效地解决了重复控制系统控制性能与系统稳定性之间的折衷问题，即使得乘性不确定性系统具有鲁棒稳定性又提高系统的扰动抑制性能和跟踪性能.将本文所提出的方法与文献［10－11］的方法均应用于低频线振动台系统，仿真结果验证了本文所提的方法具有更高的跟踪精度，更具有实用性，并且使得系统具有鲁棒性.

1 问题描述

设控制系统如图1所示.其中，r，e，u，d，θ分别为参考输入、输出误差、控制输入、扰动信号、输出信号.z1，z2为评价输出.P(s)为被控对象的标称模型，Δ(s)是被控对象未知的摄动函数(‖Δ(s)‖∞≤1)，W2(s)表示Δ(s)的摄动界函数.M(s)是重复控制器，K(s)是输出反馈控制器.d与θ存在非线性关系，即存在周期函数H(·)，使得d=H(θ)，它实际上构成了非线性反馈.

图1 含有重复控制器的控制系统

本文考虑的问题是设计重复控制器M(s)和输出反馈控制器K(s)，抑制未知的周期性扰动d，提高系统的跟踪精度.在图1中设计重复控制器就是设计合适的低通滤波器Kq(s).

2 重复控制系统鲁棒性能分析

2.1 控制系统鲁棒稳定性分析

定理1 设被控对象P(s)含有稳定摄动Δ(s)，且满足‖Δ(s)‖∞≤1，当图1的重复控制系统满足

则重复控制系统对于任意Δ(s)是鲁棒稳定的.

证明 考虑系统的鲁棒稳定性，设r=d=0.从图1中可以得到从w2到z2的传递函数为Gz2w2=－W2(s)T(s)，然后利用小增益定理可以得到:当‖Gz2w2‖∞=‖W2(s)T(s)‖∞＜1时，重复控制系统对于任意Δ(s)是鲁棒稳定的.证毕.

2.2 控制系统扰动抑制性能分析

扰动抑制的目标是尽量减小扰动输入d对评价输出z1的影响，即实现

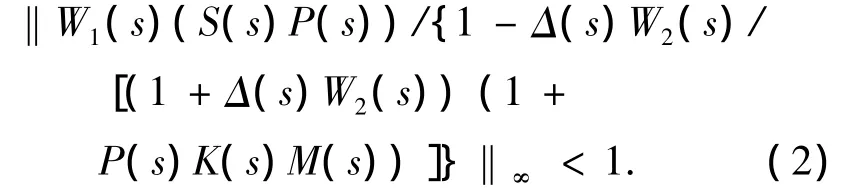
其中:S(s)=(1+P(s)K(s)M(s))－1.

由于Δ(s)在‖Δ(s)‖∞≤1的范围内可任意取值，因此即使鲁棒稳定条件成立，仍会存在这样的Δ(s)，使得在某些频带上

显然，对于该摄动Δ(s)，扰动抑制会极端恶化，所以，即使标称系统性能和鲁棒稳定性再好，也不能保证鲁棒扰动抑制性能.

因此为实现扰动抑制性能，(1)和(2)必须同时满足.由于(2)中含有摄动项Δ(s)，在设计时，必须把这个条件转变成不含摄动的一个条件，因此乘性摄动系统的扰动抑制性能问题等价于导入假想摄动Δf(s)(如图2所示，其中‖Δf(s)‖∞＜1)后的鲁棒稳定问题.

因为‖e－τs‖∞=1，因此将图2中的摄动Δf，Δ和e－τs分离出来.通过把图2变形为图3，鲁棒抑制问题归结为对具有对角结构型摄动的重复控制系统鲁棒稳定性问题.

图2 等价鲁棒稳定问题

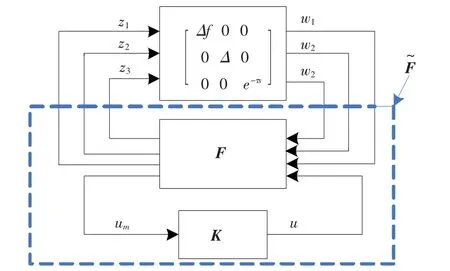
图3 鲁棒稳定性与鲁棒性能

设被控对象P(s)的状态空间表达式为

其中:xp∈Rn是被控对象的状态向量，u∈Rm是控制输入.

设扰动抑制加权函数W1(s)的状态空间表达式为

设鲁棒稳定加权函数W2(s)的状态空间表达式为

选择广泛使用的低通滤波器Kq(s)=ωc/(s+ωc).

将低通滤波器Kq(s)转化成如下的状态空间表达式:

考虑图3的重复控制系统的鲁棒稳定性，可以令r=0.

利用(3)～(6)可以得到广义被控对象F:

其中:

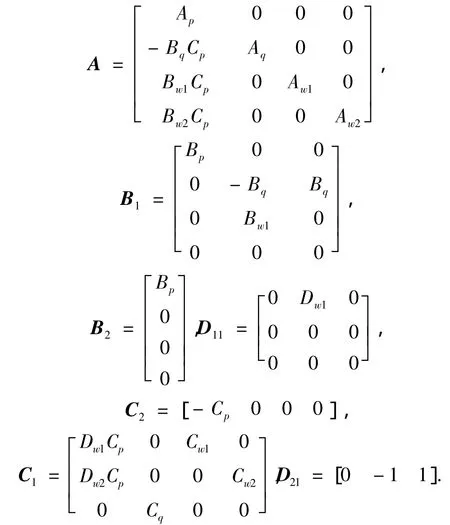
设广义被控对象(7)的输出反馈控制器K(s)的状态空间表达式为

其中:

由于‖diag(Δf，Δ，e－sT)‖∞≤1，根据小增益定理可知，图3所示的闭环系统鲁棒稳定性的充分条件为

引理1［13］设γ＞0，且G(s)的最小实现由(A，B，C，D)给出，则A是稳定阵，且‖G(s)‖∞＜γ的充要条件是存在X＞0满足

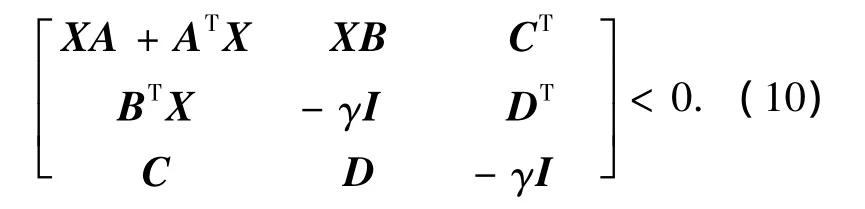
定理2 设γ=1，Gzw由式(9)给出.如果存在

证明 设γ=1，Gzw由式(9)给出.由引理3的充分条件可以得到定理2的证明.证毕.

由于定理2使用对角型结构的摄动，导致保守性较大.鉴于此，在图3中引入定标阵Q= diag(Q1，Q2，Q3)，再利用小增益定理来确定系统鲁棒稳定性的充分条件.在图3中加入稳定的定标阵变形为图4.

图4 导入定标阵的结构图

设Q=diag(Q1，Q2，Q3)，利用小增益定理可知图4的闭环系统鲁棒稳定的充分条件为

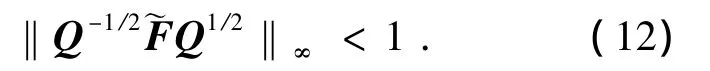
满足式(12)的定标矩阵Q的条件归结为如下LMI:

3 控制器设计

定义矩阵

定义变量:

式(13)变换成以下LMI:

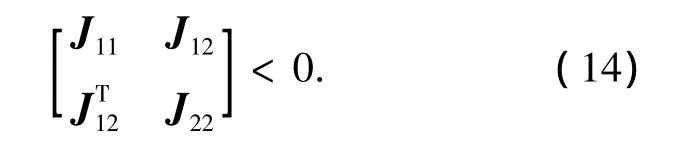
其中:

注:矩阵不等式(14)不是线性的，无法便捷地得到控制器参数和ωc，下面的推论1给出了将非凸的矩阵不等式(14)转化为非线性最小化问题求解.

推论1 给定一个参数ωc，将(14)转化为如下的非线性最小化问题:

S.t.:

若其解为m+2且存在正定矩阵Q，Q1，R，S，则得到所要求的控制器参数表示矩阵的迹.

在上述的锥补线性化方法中很难通过数据方法保证min tr(Q·Q1)精确的等于m+2，所以用式(14)作为迭代终止的判定条件.下面给出具体的算法1:

2)求解如下的线性矩阵不等式最小化问题:

令求出的解为

3)将求出的解带入式(16)，如果满足，则得到控制器增益若不满足，且迭代次数大于设定的最大迭代次数 jmax，则系统无解，否则令j=j+1，转到2).

理论上重复控制系统中低通滤波器的剪切频率越大，系统的跟踪精度越高［11］，因此可以利用下面的算法2得到ωc的最大值及其对应的Ak，Bk，Ck.算法2的步骤如下:

1)首先确定算法1的最大迭代次数jmax，ωc的增加值Δωc＞0，1＞Δωc2＞0，给定一个很小的ωc及算法2终止参数ε.

3)ωc=ωc+Δωc，利用算法1的方法求解如果有解，转到3);如果无解，转到4).

4)ωc，利用算法1的方法求解.如果无解，转到4).如果有解，转到3).当Δωc＜ε时(一般ε选得很小)，转到5).

5)通过矩阵I－RS的奇异值分解，得到满足MNT=I－RS的M，N.

6)从(14)式计算镇定控制器参数Ak，Bk，Ck.

注1:文献［10］提出一种求解低通滤波器剪切频率ωc的算法，首先给定一个正定矩阵Q和标量μ＞0，然后利用LMI求解ωc.由于正定矩阵Q和标量μ＞0是人为给定的，因此该方法具有很大的保守性.文献［11］的方法比文献［10］的方法求解ωc的保守性小，但是没有考虑系统的扰动抑制问题.本文提出的设计方法利用二分法逐渐寻找ωc的最大值及其对应的输出反馈控制器参数，此方法没有人为给定的参数，因此求解的ωc保守性小，并且使得系统的扰动抑制性能更强.

4 应用实例

为了验证本文所提方法在实际应用中的有效性，对低频线振动台进行仿真研究，永磁直线同步电机(PMLSM)是其驱动部件，PMLSM的传递函数为可测反馈信号为低频线振动台的位置信号θ，期望轨迹为正弦信号0.1sin(10πt).外部扰动信号可写成

其中:

设乘性不确定性 W2(s)=0.7(0.05s+ 1)/(0.035s+1)，扰动抑制加权阵W1(s)= 100/(0.8s+1).

给定算法1和算法2的参数:Δωc=100，Δωc2=0.1，ε = 1，ωc= 0，jmax= 100.得到ωcmax=1 638，与ωcmax对应的输出反馈控制器为K(s)=

简化后为

为了验证本文所提出方法的有效性，用文献［10］和文献［11］提出的方法与本文所提出的方法做比较.针对低频线振动台，文献［11］的方法没有可行解.利用文献［10］的方法设计低频线振动台的重复控制器时，设系统不含不确定性，首先给定系统的镇定控制器为及然后利用LMI的方法求得γ=2.208 4×104.

针对低频线振动台，采用本文所提出的方法设计的重复控制系统的位置误差和采用文献［10］提出的方法设计重复控制系统的位置误差如图5所示.

图6为采用本文所提出的方法设计的重复控制系统的加速度频谱图.

图5 鲁棒重复控制的仿真结果

图6 重复控制的低频线振动台加速度频谱图

很明显，本文所提出的重复控制系统设计方法提高了低频线振动台的跟踪性能.通过图6可知低频线振动台的加速度失真度为1.34%，满足系统的性能指标.

5 结论

本文提出的重复控制器和输出反馈控制器的设计方法有效地抑制了乘性不确定性系统存在的周期性扰动，提高了系统的跟踪性能.给出了计算重复控制器中低通滤波器最大的剪切频率及其对应的输出反馈控制器参数的迭代算法.仿真结果验证该设计方法的有效性.

［1］FRANCIS B A，WONHAM W M.High accuracy control of a proton synchrotron magnet power supply［J］.Applied Mathematices＆Optimization，1975，2(2):216－221.

［2］PEDRO R S，ENRIQUE A.Dynamic voltage restorer based on flying capacitor multilevel converters operated by repetitive control［J］.IEEE Transactions on Power Delivery，2009，24(2):951－960.

［3］FUJIMOTO H.RRO compensation of hard disk drives with multirate repetitive perfect tracking control［J］. IEEE Transactions on Industrial Electronics，2009，56 (10):3825－3831.

［4］ABRAHAM D R，HENDRIK T.Mouton and Hirofumi Akagi.DFT－based repetitive control of a series active filter integrated with a 12 pulse diode rectifier［J］.IEEE Transactions on Power Electronics，2009，24(6):1515－1521.

［5］GOELE P，BRAM D，FARID A B，et al.Optimal performance tradeoffs in repetitive control:experimental validation on an active air bearing setup［J］.IEEE Transactions on Control Systems Technology，2009，17 (4):970－979.

［6］HARA S，YAMAMOTO Y，OMATA T，et al.Repetitive control system:A new type servo system for periodic exogenous signals［J］.IEEE Transactions on Automatic Control，1988，33(7):659－666.

［7］张东纯，曾鸣，苏宝库.精密速率控制系统中位置周期扰动的动态补偿一种有限维重复控制方法［J］.宇航学报，2003，24(1):57－60.

［8］GUVENC L.Stability and performance robustness analysis of repetitive control systems using structured singular values［J］.ASME Journal of Dynamic Systems，Measurement，and Control，1996，118(9):593－597.

［9］CHEN J W，LIU T S.H∞repetitive control for pickup head flying height in near－field optical disk drives［J］.IEEE Transactions on Magnetics，2005，41(2):1067－1070.

［10］WEISS G，ZHONG Q C，GREEN T C，et al.H∞repetitive control of DC－AC converters in microgrids［J］. IEEE Transaction on Power Electronics，2004，19(1): 219－230.

［11］吴敏，兰永红，佘锦华，等.线性不确定系统的H∞状态反馈鲁棒重复控制［J］.控制理论与应用，2008，25(6):427－433.

［12］梅生伟，申铁龙，刘康志.现代鲁棒控制理论与应用［M］.北京:清华大学出版社，2003.

［13］DOH T Y，RYOO J R，CHUNG M J.Design of a repetitive controller:an application to the track－following servo system of optical disk drives［J］.IEE Proc.Control Theory and Applications，2006，153(3):323－330.