直驱式电液伺服转叶舵机的遗传蚁群参数辨识
苏文海,姜继海
(1.东北农业大学工程学院,哈尔滨150030;2.哈尔滨工业大学机电工程学院,哈尔滨150001,hitswh@163.com)
传统的转叶舵机[1-2]控制方式主要有比例阀控制和变量泵控制两种方式,对液压系统的清洁度要求高,控制系统复杂,控制元件多,容易发生故障[3].针对传统转叶舵机伺服系统的弊端,哈尔滨工业大学提出并制造了直驱式电液伺服(DDEH)转叶舵机[4-5].与传统的转叶舵机相比,DOEH转叶舵机用变频电机驱动定量泵取代了异步电机驱动变量泵或者伺服阀的控制方式,对系统清洁度要求大大降低.同时,直驱式电液伺服舵机去掉了泵站和管路,减少了控制元件,占地面积更小,系统的可靠性更高,节约能源且绿色环保,是新型高效的舵机形式,但是目前尚没有适用的系统模型.因此,建立直驱式电液伺服转叶舵机的数学模型并对模型参数进行辨识,对研究直驱式电液伺服转叶舵机的动、静态特性和进一步提高其控制性能的理论分析有很大意义.
本文首先建立直驱式电液伺服转叶舵机的数学模型并确定模型阶数,然后使用遗传蚁群算法(ACO-GA)对模型参数进行辨识,并将辨识结果用另一组实验数据进行检验,验证辨识参数的可靠性及实用性.
1 直驱式电液伺服转叶舵机数学模型
直驱式电液伺服转叶舵机在建立数学模型时按变频调速部分、液压动力机构、舵机加载等环节分别建立各环节的动态方程,综合后得到直驱式电液伺服系统的数学模型.

式中:KV为电压频率转换系数,Hz/V;Kf为频率电压转换系数,V/Hz;JT为折算到电机轴的转动惯量,kg·m2;TLT为电机的负载转矩,N·m;BT为电机转轴阻尼系数,N·ms/rad;KT扭转弹性转矩系数,这里KT≈0;θp为电动机转子的扭转角位移;ωp为转子机械角频率,rad/s;TE为电磁转矩,N·m;KE1,KE2为交流电机定常系数;Dp为定量泵的排量,m3/rad;P1为泵的出口压力,Pa;Pr为泵的入口压力,Pa;ηpm为机械传动效率,取ηpm=0.9;ηpv为定量泵的容积效率,m3/rad;Dm为转叶马达的排量,m3/rad;θm为马达轴转角,rad;V0为一个腔室的容积,m3;βe为有效体积弹性模量,N/m2(Pa);Ct为总的泄漏系数(m3/(s·Pa); Jm为马达和折算到马达轴上的总惯量,kg·m2;Bm为粘性阻尼系数,N·m·s/rad;TL为外负载力矩,N·m;pL为加载装置中溢流压力,Pa.
联立式(1)~(7)得到直驱式电液伺服转叶舵机的方块图如图1所示.

图1 直驱式电液伺服转叶舵机的方块图
将TL看做直驱式电液伺服转叶舵机的干扰,则舵机的转角θm可表示为

空载时,即负载力矩TL=0,则有

式中:
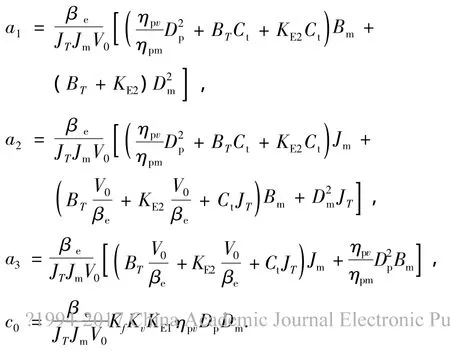
从式(8)可以看出,直驱式电液伺服转叶舵机是四阶系统.
2 ACO-GA参数辨识方法
ACO-GA算法的实现过程是首先由遗传算法产生一个较优解,较优解的路径留下信息素,其他不改变;然后让蚂蚁按照蚁群算法[6-7]完成一次遍历后,再让蚂蚁做遗传算法的交叉和变异操作,得到新的路径,计算每只蚂蚁走过的路径所生成的解的适应度,如果新生成的蚂蚁的适应度值小于原来较优解的适应度值,则在此蚂蚁遍历的节点上留下信息素.
2.1 连续系统的离散化
对系统进行辨识的主要依据是系统的实验数据.由于这些数据是离散非连续的.所以在辨识前需要将待辨识的连续型系统模型变成离散化的模型才能使用辨识数据.这里使用双线性变换公式对系统进行离散化,双线性公式如式(10)所示:

式中:T为采样周期,s为拉式变换中的s.
将式(10)代入式(9),并取输入到输出的时间延迟为1个采样间隔,经过整理可以得到:
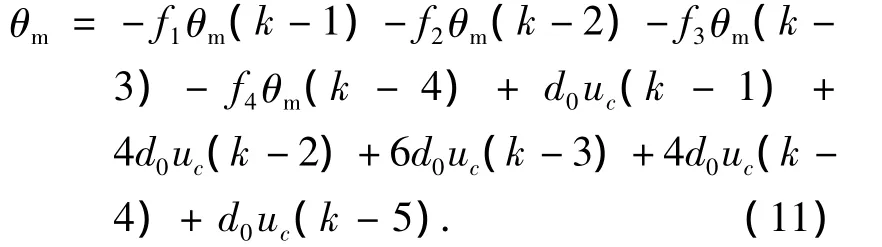
式中:


其中:f0=-2a1T3+4a2T2-8a3T+16.
将式(11)中相关系数写成向量形式,有
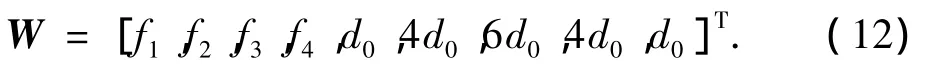
将系统的输入输出变量用如下向量表示:

则ACO-GA辨识器输出可用下式表示:

根据经验和理论推导,制定式(12)中向量的取值范围.W取值的上下界限Wmax和Wmin为

2.2 适应度函数及其标定
由式(13),可以制定适应度函数为

2.3 遗传蚁群算法模型参数辨识步骤
用于直驱式电液伺服转叶舵机参数辨识的遗传蚁群算法步骤如下:
步骤1 利用遗传算法产生一个较优解,在这个路径上留下信息素.
步骤2 迭代次数nc置零,将m=20个蚂蚁置于10个顶点上.
步骤3 将各蚂蚁的初始出发点置于当前解集中,对每个蚂蚁k(k=1,2,…,m)按式(14)移至下一顶点j,最终所有蚂蚁完成一次遍历;
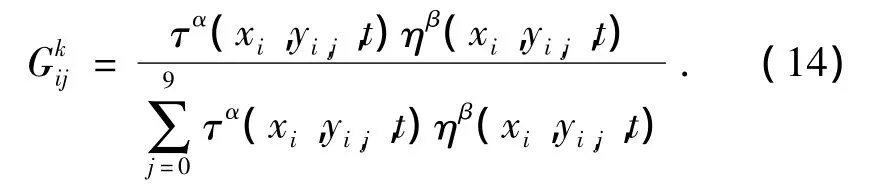
式中:τ(xi,yi,j,t)表示t时刻在节点Knot(xi,yi,j)上遗留的信息素,α为信息启发式因子,β为期望启发式因子,分别表示信息素的浓度和能见度在转移概率中的相对重要性,η(xi,yi,j,t)为节点Knot(xi,yi,j)上的能见度.
步骤4 根据交叉概率,选择若干组解进行分组交叉,若新的目标函数更优,接收新解,否则拒绝.
步骤5 根据变异概率,判断是否变异,变异后的目标函数更优,接收新解,否则拒绝;
步骤6 计算各蚂蚁的目标函数,记录当前最好解.
步骤7 对目标函数小于上次优化最好解的路径,按式(15)更新各路径点上的信息素:

式中:Fk为第k只蚂蚁在本次循环中的目标函数值,Fbest为本次循环前的最优目标函数值,ρ为信息素挥发系数.
步骤8 nc←nc+1.
步骤9 若nc小于预定的迭代次数且无退化行为,转步骤2.
步骤10 输出目前最好解.
3 辨识结果与验证
系统辨识输入数据如图2所示,为系统输入部分长为10 s,采样时间0.05 s,共2 000组采集数据.使用图2所示的输入数据及相应的输出采样数据,按照遗传蚁群算法得到一组辨识数据为W=[-3.328 0,-4.892 5,1.930 9,4.652 4,3.946 3×10-5]T.
辨识得到最优个体所对应的系统辨识输出和输出误差如图3、4所示.可以看出,在迭代所得最优个体的辨识输出能很好地跟踪实际采样值,误差在零值附近波动.
由于上述辨识结果是一组数据得到的,所以不能表明所得到的辨识模型在任一组输入数据下,其输出能很好地复现实际系统在相应输入下的输出.因此还有必要进一步对辨识结果进行验证,看其是否能与此系统上所有的采集数据一致.为不失一般性,使用另一组不相关信号加载的实验曲线去验证.系统输入项uc如图5所示.将上述辨识结果和输入项代入式(13)进行迭代,得到一组迭代输出,也即验证输出,如图6所示,验证误差如图7所示.图中验证误差是指验证输出和实际采样输出的差.

图2 变频器输入电压
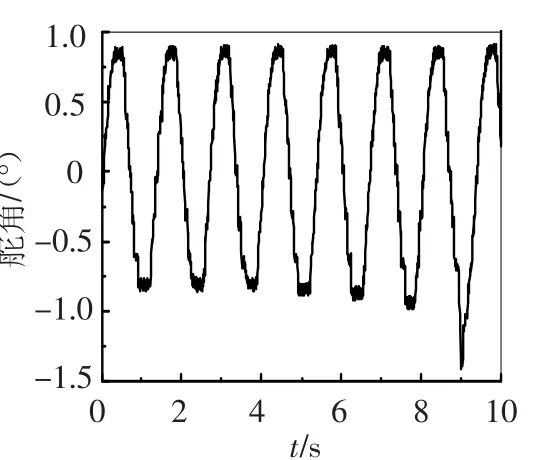
图3 最优解的辨识输出

图4 最优解的辨识误差

图5 验证输入

图6 验证输出

图7 验证输出误差
从图6和图7可以看出,验证输出和实际采样输出曲线相一致,辨识系统在新的输入项uc,其输出能够很好地逼近与输入相对应的采样输出,误差基本上控制在15%以内.由此可以看出,此辨识参数所得到的模型在系统输入作用下,能够较好地复现真实系统的输出.
4 结论
1)给出了直驱式电液伺服转叶舵机数学模型,确定了模型的阶数,用遗传蚁群算法对直驱式电液伺服转叶舵机的模型中参数进行辨识,并用实际系统采样数据进行了验证.
2)使用遗传蚁群算法的参数辨识数据拟合度为87%,拟合误差基本控制在15%以下.
3)遗传蚁群算法可以用于一般复杂系统的实际参数辨识.
[1]谢良喜,孔建益,熊和根等.转叶式液压舵机的关键技术分析.航海工程,2008,l37(4):1-34.
[2]WAGNER P,JEANNINE A.Evolution of a Modern Naval Steering System[J].Naval Engineers Journal,1987,99(3):55-64.
[3]祁联仲.舵机液压油污染的分析及控制[J].海军航空工程学院学报,2006,21(6):618-622.
[4]苏文海,姜继海,刘庆和.直驱式电液伺服转叶舵机系统分析及仿真[J].东北大学学报,2008,29(S1): 224-271.
[5]SU Wenhai,JIANG Jihai.Adaptive Fuzzy Sliding-Mode Control for Direct Drive Electro-Hydraulic Servo Rotary Vane Steering Gear[C]//The First International Workshop on Intelligent Systems and Applications.Wuhan,China:IEEE,2009:531-535.
[6]DEMIREL N C,TOKSARI M.Optimization of the quadratic assignment problem using an ant colony algorithm[J].Applied Mathematics and Computation 2006,183 (1):427-435.
[7]段海滨,王道波,于秀芬.基于云模型的小生境MAXMIN相遇蚁群算法[J].吉林大学学报(工学版),2006,36(5):803-808.

