一种电容式闭环微加速度计系统
陈伟平,王天阳,尹 亮,陈晓亮,郭玉刚,刘晓为
(哈尔滨工业大学MEMS中心,哈尔滨150001,wangtianyang1986@163.com)
随着硅微加工技术的不断成熟,硅加速度计已经在传感器市场占据着越来越重要的地位,小型化、智能化、集成化已成为加速度传感器的发展方向,其应用也逐步扩展到各个领域[1].十几年来,尽管在微加速度设计和制作工艺等方面进行了很多有意义的研究[2-4],但在系统控制方面的研究还是比较有限的[5].典型的电容式加速度传感器结构是由两个固定电极和一个可动电极组成,可动电极作为公共极板与两固定电极形成一对差分电容.当有加速度作用时,可动极板就会偏离平衡位置,从而使差分电容产生与加速度成比例的不平衡输出,通过检测此输出即可测得加速度的大小.这种开环加速度传感器结构比较简单,但在系统带宽、线性度和动态范围等方面受到很大限制.一种有效的解决办法就是应用闭环控制系统,在固定极板上加一反馈力,使其保持在平衡位置,通过检测反馈力即可测得加速度的大小[6].这种闭环微加速度传感器具有线性度好、动态范围大等优点,广泛应用于高精度的加速度计设计中.本文在一种梳齿电容结构的基础上,建立了闭环系统的数学模型,并在系统的设计中引入PID控制补偿,通过仿真分析研究了PID控制参数对系统的影响,大大提高了加速度传感器的性能.
1 加速度传感器结构
基于ICP刻蚀和键合工艺设计的传感器结构如图1所示,该结构包括上下固定电极和与H型质量块相连的可动电极组成.质量块通过折叠梁与左右键合块连接.该结构具有敏感质量大、检测电容大、灵敏度高等优点.理论分析和仿真给出该 结构的主要性能参数如表1所示.

表1 传感器结构参数
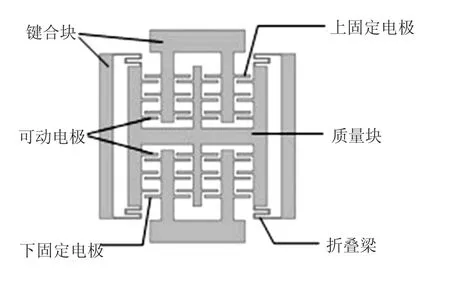
图1 传感器结构示意
2 闭环加速度计系统
2.1 微结构模型
传感器微结构模型如图2(a)所示,利用经典的二阶系统等效模型可得敏感结构部分的传输函数为
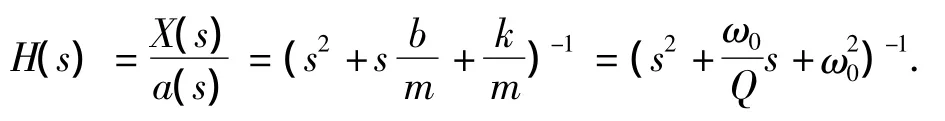
式中:x为质量块位移;ω0,为固有角谐振频率;,为品质因数.
为对系统工作原理进行分析,将微结构等效为四个电容,如图2(b)所示,电容C1和C2极板间距为d,C3和C4极板间距为md(m为常系数).在非公共端的两个电极上,分别施加电压V+,V-.当有加速度a输入时,由于加速度作用,质量块将偏离平衡位置,假设它向C1方向移动了Δd的位移,则4个电容都将随活动电极与两个固定电极之间距离的变化而变化[7].
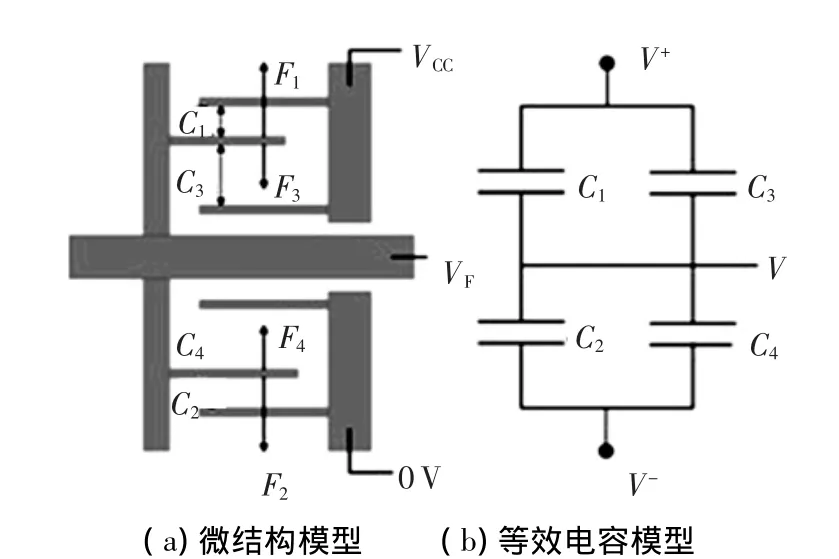
图2 传感器微结构及等效电容模型
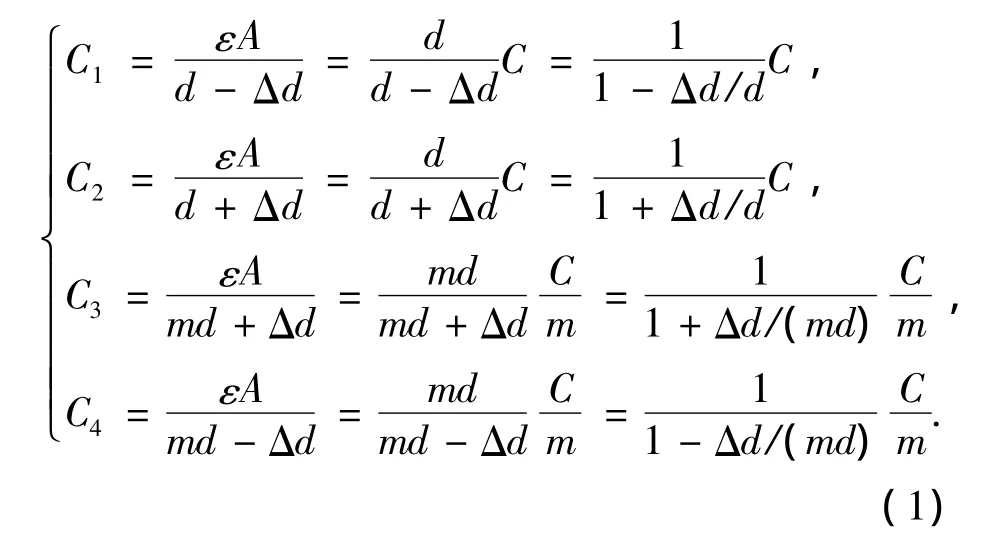
调制信号V+,V-分别为
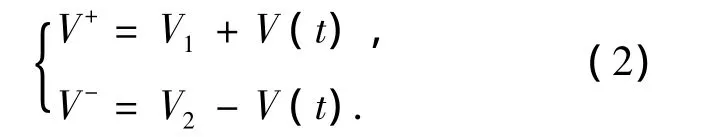
由式(1)和式(2)和可以得出
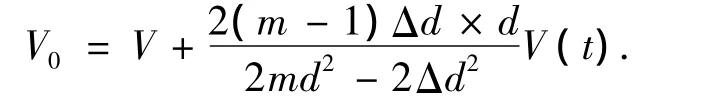
其中V为低频信号,由于解调后不会输出,这里未作详细介绍.由于Δd比d要小两到三个数量级,则Δd2要比md2小四个数量级.它对灵敏度的影响不大,只会影响到传感器输出电压的非线性.
因此,只考虑传感器灵敏度时,上式可以近似为
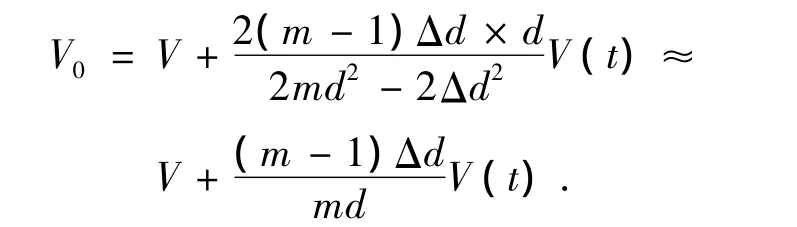
2.2 力平衡反馈
力反馈过程的示意图如图2(a)所示.固定上极板接电源电压VCC,下极板接零电位,VF为反馈电压,也是传感器的输出电压V0.由于梳齿的非均匀分布,两侧的固定梳齿对中间活动梳齿共有四个力的作用,即图中所示F1,F2,F3,F4.
根据平行板间静电力的计算,极板间产生的静电力F为
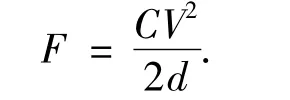
其中:C为电容;V为极板间所加的电压;d为极板间距离.随着反馈电压VF的变化,极板间电压V将发生变化,这4个静电力的大小也都随之变化.建立相应模型,可以得到它们的合力为
通过“老年人生活质量评定表”从身体健康、心理健康、社会适应和环境适应4个方面来获取老年人生活质量状况。
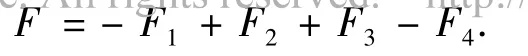
2.3 系统模型
对于连续时间系统,输出信号和反馈信号都加在可动极板上,要通过频域加以区分.加在结构的固定极板的差动载波信号将变换信号调制到高频,这样可以很好的减小低频噪声.输出的信号经过前级放大,同步解调之后,低通滤波器将高频成分过滤掉,得到与输入加速度成比例的电压信号.
由上述分析建立系统仿真模型如图3所示[8-9],模型中的处理电路模块包括调制解调器以及二阶低通滤波器.引入PID控制器用来对系统进行补偿,经典的PID控制器传输函数G(s)由三条并行通路组成,按偏差的比例(Proportional)、积分(Integral)、微分(Derivative)控制,简称PID控制.PID控制广泛应用于过程控制中,其控制参数分别为KP,KI和KD[10]关系不式如下:
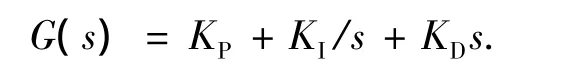
设反馈增益为KF,低通滤波器的传输函数为HF(s).由此,根据图3所示模型,可以写出系统的开环传输函数为
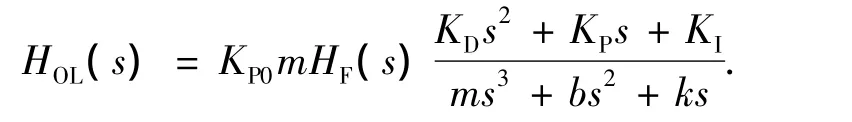
式中:KP0为系统增益常数.
闭环传输函数可写为
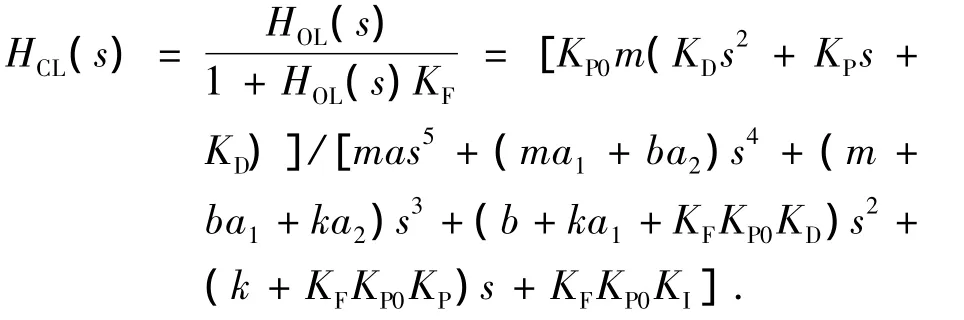
式中:a1和a2为二阶低通滤波器的系数.
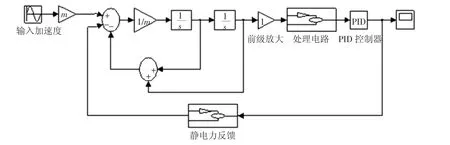
图3 闭环系统仿真模型
与开环传输函数相比,闭环增益减小到开环增益的1/(1+HOL(s)KF),所以在相同加速度的作用下,敏感质量的位移也相应减小,这样就提高了系统的线性度和分辨率.由闭环系统的传输函数可以看出,敏感结构的参数(弹性系数k和阻尼b)越小,PID控制器对系统的控制作用越强,所以高性能的闭环加速度传感器要求敏感结构具有较小的弹性系数和阻尼系数.
3 仿真分析
3.1 系统正弦响应分析
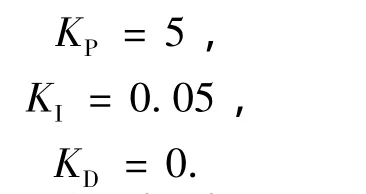
PID控制器增大了系统反馈,使系统的增益稍小,但是积分器对系统的相位补偿作用显著,大大减小了系统的延迟.
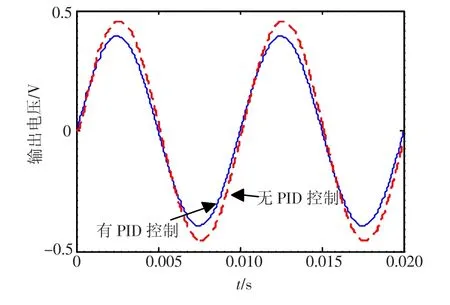
图4 系统输出响应对比
3.2 系统阶跃响应分析
由自动控制理论可以知道[11],PID控制器可以改善系统的阻尼,调节系统的上升时间和调节时间.KP=5,KI=0.05,KD=0.002 5时的系统阶跃响应曲线如图5所示,图中同时给出了无PID控制器时系统阶跃响应,输入信号阶跃时间在0.000 5 s,阶跃值为1 g.可以看到PID控制器对系统阶跃响应的控制作用,大大减小了系统的响应时间和调节时间.
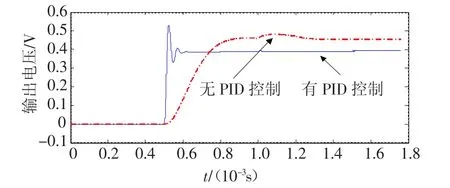
图5 系统阶跃响应对比
4 实验结果
设计得到的加速度传感器结构由于工艺偏差等原因,是一个欠阻尼器件.通过PCB板连接带有PID控制模块的接口电路进行了阶跃响应测试.图6(a)是PID调整之前的系统阶跃响应测试结果,可以看出系统是一个欠阻尼系统,阶跃响应出现了不希望得到的震荡.
通过调整接口电路的PID模块参数,将系统调节到了临界阻尼状态,消除了震荡并且保证系统具有最快的响应速度,大大提高了系统性能.图6(b)是经过PID调整后的阶跃响应测试结果.
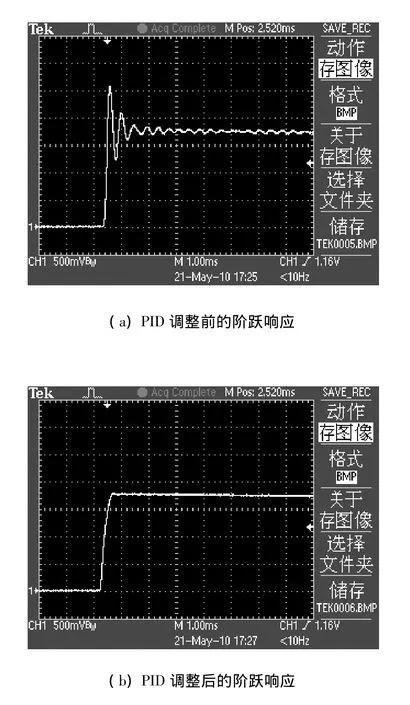
图6 阶跃响应实验波形
5 结论
本文设计了一种基于梳齿电容式微加速度计结构的闭环控制系统,分析了传感器的等效电容模型及其力反馈模型,在控制系统中引入了PID控制器,并建立了系统的开环和闭环传输函数.利用SIMULINK模型对系统进行仿真,分析了PID控制器对相位的补偿作用和对系统阶跃响应的控制作用.实验结果表明PID控制器的引入可以大大提高传感器系统的性能.
[1]陈渝,郁发新,王慧泉,等.电容式力平衡加速度计的设计[J].传感技术学报,2006,19(2):411-412.
[2]YAZDI N,NAJAFI K.An all-silicon single-wafer microg accelerometer with a combined surface and bulk micromachining process[J].Journal of micro electromechanical systems,2000,9(4):544-550.
[3]BOSER B E,HOWE R T.Surface micro-machined accelerometers[J].Journal of solid-state circuits,1996,31(3):366-373.
[4]LEE I,YOON G H.Development and analysis of the vertical capacitive accelerometer[J].Sensors and actuators A,2005,119:8-18.
[5]KRAFT M,LEWIS C P.Design of a hybrid closed loop control system for a MEMS accelerometer using backstepping principle[C]//Microelectronics,2007.ICM 2007.International Conference.London:[s.n.],2007:213-216.
[6]KRAFT M,LEWIS C P,HESKETH T G.Closed-loop silicon Accelerometers[J].IEEE Proceeding Circuits,Devices and System,1998,146(5):325.
[7]陈伟平,赵振刚.力平衡框架结构加速度计的设计[J].传感技术学报,2006,19(5):2193-2195.
[8]PARK K M.Methodologies for MEMS device performance and damage monitoring[D].Hoboken:Stevens institute of technology,2002.
[9]AALTONEN L,PAHIKKALA P.Continuous time interface for±1.5 g closed-loop accelerometer[C]//Integrated circuit design and technology.2007.ICICDT’07 IEEE International Conference.Austin,TX:[s.n.],2007:1-4.
[10]FRANKLIN G F,POWELL J D.Abbas Emami-Naeini.Feedback control of dynamic systems[M].4th ed.朱齐丹,张丽珂,译.北京:电子工业出版社,2004.
[11]KUO B C,GLONARAGHI F.Automatic control systems[M].汪小帆,李翔,译.北京:高等教育出版社,2004.

