食用油红外光谱的分形维数特征
孙翘楚,肖创柏,郭 犇,苏 峰
(1.北京工业大学计算机学院,北京100124,sunqiaochu@hotmail.com;2.中国农业银行总行软件开发中心,北京100073)
近年来,红外光谱技术在食品鉴别方面的应用研究发展迅速.红外光谱技术的优势在于样品几乎不需要分离处理,从而使得鉴别过程更加迅速[1].同时根据样品成分的红外吸收率,红外光谱技术能够提供整体信息来鉴别样品.红外光谱根据不同的波数范围分为近红外(12 900~4 000 cm-1)、中红外区(4 000~650 cm-1)和远红外区(650~10 cm-1)3个光区.其中,中红外区是应用最早和最广的一个区,大多数有机化合物和无机离子的基频振动吸收都落在中红外区内.化合物分子中所含的化学键或官能团不同,或官能团所处的化学环境不同,其振动能级从基态跃迁到激发态所需能量不同会吸收不同波长的红外光,形成不同的红外光谱图,而相关吸收峰的高度与其含量成正比.因此,红外光谱法被广泛用于有机物的定性和定量研究.由于傅里叶变换红外光谱法(Fourier transform infrared spectroscopy,FTIR)具有整体、快速、无损鉴定复杂体系多种组份的特点,目前己在食品鉴别领域获得了广泛应用[2-3].
刘沭华等[4]通过对几种中药的傅里叶变换红外光谱进行求一阶导数对其进行区分.但是在本文初期实验中,这种方法并不适合食用植物油的红外光谱.对其求一阶导数并不足以对其区分.同时对各个光谱的指纹区进行了积分操作,提取的特征差别细微,不足以作为区分的标准.贾素贞等[5]通过对几种食用植物油的二维傅里叶变换红外光谱进行特征提取,对其进行区分.这种方法可以很好的放大一维光谱的差异,但是计算复杂,对设备要求较高.本文提出一种利用分形理论提取食用植物油红外光谱特征的算法,将此作为一种主要特征引入食用油红外光谱模式识别中,在实验中取得了较好效果.
1 基于分形理论的红外光谱特征提取
1.1 盒维数定义
分形学的概念的实质是除传统几何学以外的不规则几何体在标度变换下的自相似性.
若F是分形集,则其应具有以下性质[6]:
1)F具有精细结构,即有任意小比例细节;
2)F极不规则,以致其整体与局部都无法用传统几何语言描述;
3)F通常具有某种自相似性;
4)F的分形维数大于其拓扑维数;
5)F可以用非常简单的方法定义,可以由迭代产生.
一般而言若研究对象符合上述性质中的全部或大多数,即使有某个性质例外,也并不影响称其为分形.
计盒维数或称盒维数(Box-counting or Box dimension)是应用最广泛的维数之一,它的普遍应用主要由于这种盒维数的数学计算以及经验估计相对容易.
盒维数的定义为:设F为Rn中任一非空子集,记N(F,δ)表示最大直径为δ且能覆盖F的集合的最小数,则F的上下盒维数分别定义为

如果上下维数相等,则称这个共同的值F的计盒维数或者盒维数,定义为
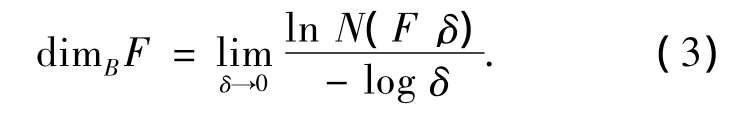
盒维数存在一些等价定义,有时这些定义更适合应用.通常为以下五种[7]:
1)覆盖F的半径为δ的最小闭球数;
2)覆盖F的边长为δ的最小立方块数;
3)相交于F的δ-网格块数;
4)覆盖F的直径至多为δ的最小集合数;
5)球心在F中半径为δ的互不相交球的最大数.
本文利用定义(3)对红外光谱的分形维数进行计算.
1.2 盒维数的计算
设A∈H(X),其中,(X,d)是度量空间,εn=cbn,0<b<1,c>0和n=1,2,3,….
如果

则A具有分形维数D.在式(4)中用γ代替ε,计算分形维数的公式为

故可让ln N(A,γ)与ln γ成为一对变量,则式(5)变为

于是D(A)就成了(ln γ,ln N(A,γ))坐标系统中的斜率[8].本文借以不同红外光谱盒维数的不同,对其所代表的食用油进行区分.
1.3 红外光谱分形维数计算方法
红外光谱在计算机中以图像的格式存储,文中使用Intel公司开发的OpenCV开源计算机视觉库,实现了红外光谱的分形维数计算.具体其分形维数计算过程如图1所示.

图1 红外线光谱盒维数计算流程图
1)首先读入光谱图像,对光谱图像进行二值化处理[9].原始红外光谱图像为彩色图像,进行盒维数计算时,应先将彩色图像转换成二值图像(如图2所示).利用OpenCV的on-trackbar()函数生成滑动条,动态设定阈值,阈值的取值以能显示全部光谱图像为准.然后利用cvThreshold()函数将读入图片二值化.包含光谱的像素点值为0.

图2 二值化后的光谱图像(局部)及其对应的二值数据
2)将得到的二值图像转存为矩阵.运用cv-Convert()函数将二值图像转存为与其同尺寸的矩阵I.
3)把得到的矩阵依次划分为若干块,每一块的行数与列数均为 k,k取 1,2,4,…,2n,运用cvGetReal2D()函数扫描每个划分块,把包含像素0的块的个数记为Nk.这样就得到k与Nk的对应数组B[10].
4)对数组B中的元素求对数.并在双对数坐标平面中,以一元线性回归用直线拟合数据点(ln k,ln Nk),k=1,2,4,…,2n,所得到的斜率的负值D就是该红外光谱的盒维数.
2 实验结果及分析
2.1 算法正确性检验
通过实验发现,分形维数的正确性与k的取值以及图像的分辨率有关.在实验中取1,2,4,8,16,32,64,128,256,这9个值对图像计算分形.
根据盒维数的定义,所取k的尺寸越小,所计算出的分形维数越精确.但由于对存储在计算机中的图像进行分形计算,只能分割到像素点尺寸.因此计算分形算法所得出的结果与实际分形维数之间存在误差.而误差的大小直接影响到特征提取的准确性,若计算出的误差大于光谱分形维数的差异,则无法利用此差异对光谱进行区分.为验证分形维数计算算法的准确性和可靠性,分别用直线、矩形、Koch曲线、Cantor三分集、Sierpinski三角垫和Sierpinski地毯等已知维度的分形图形对算法进行验证.结果如表1所示.

表1 分形维数计算结果
由实验结果可知,误差在小数点后三位到四位之间,而光谱分形维数的差异在小数点后两位.因此,误差不会对特征提取造成影响.
2.2 实验分析
采用本文的算法,本文对市面上常见的福临门、金龙鱼、欧尚等品牌的几种食用油的红外光谱的分形维数进行了计算.通过对每种食用油各30个样本的盒维数计算(抽样结果如表2所示,其中,k为窗口大小,Nk为盒子数),可知食用油的盒维数总体在1.293 1~1.315 3之间.可利用此特征对食用油同其他液体进行区分.另外通过对玉米油和芝麻油的红外光谱分形维数的计算得到,玉米油的红外线光谱的分形维数在1.293 1~1.297 2之间,而芝麻油的红外光谱分形维数在1.311 3~1.315 3之间,分形维数差别明显,因此可利用此特征对两种植物油的真伪进行鉴别.

表2 食用植物油红外光谱盒维数计算结果
3 结论
1)分形维数能有效地表现红外光谱的复杂度以及自相似性特征.
2)分形维数的准确性与源图像的分辨率有关,在实验中采用的光谱图像分辨率为1280× 880.随着仪器设备的不断进步,更大分辨率的光谱图像可以得到更为准确的分形维数特征.
3)通过引入其它特征,如谱峰高度、光谱导数、面积等特征,可以对其它食用油进行更好的区分.
4)通过对市面上几种常见食用油的红外线光谱的分形维数的计算表明,利用分形维数可以对玉米油以及芝麻油的真伪进行较好的区分.
[1]Van de VOORT F R,GHETLER A,GARCIA-GONZA'LEZ D L.Perspectives on quantitative mid-ftir spectroscopy in relation to edible oil and lubricant analysis:Evolution and integration of analytical methodologies[J].Food Analytical Methods,2008,3(1):153-163.
[2]MILLS B L,Van de VOORT F R,KAKUDA Y.The quantitative analysis of fat and protein in meat by transmission infrared analysis[J].Meat Science,1984,11(4):253-262.
[3]Van de VOORT F R,SEDMAN J,ISMAIL A A.A rapid FTIR quality control method for determining fat and moisture in high-fat products[J].Food Chemistry,1993,48(2):213-221.
[4]刘沭华,张学工,周群,等.近红外漫反射光谱法和模式识别技术鉴别中药材产地[J].光谱学与光谱分析,2006,26(4):629-632.
[5]贾素贞,鲍猛,聂传平.几种食用油的二维红外相关分析[J].济南大学学报,2007,21(2):124-129.
[6]BRIGGS J.Fractals:The Patterns of Chaos[M].London:Thames and Hudson,1992:148.
[7]FALCONER K.Techniques in Fractal Geometry[M].NJ,USA:John Willey and Sons,1997:59-61.
[8]张平,王新柯,李海涛,等.基于分形理论的太赫兹光谱识别[J].量子电子学报,2007,24(6):672-676.
[9]文志英.分形几何的数学基础[M].上海:上海科技教育出版社,2002.
[10]CHAUDHURI B B,SARKAR N.Texture segmentation using fractal dimension[J].IEEE Transactions on Pattern Analysis and Machine Intelligence,1995,17(1): 72-77.
[11]王韶娟,曾国荪.分形维数的一个并行算法[J].计算机应用与软件,2005,22(10):19-20.

