欠驱动AUV的鲁棒位置跟踪控制
毕凤阳,张嘉钟,魏英杰,曹 伟
(哈尔滨工业大学航天学院,哈尔滨150001,bifengyang@126.com)
自主水下航行器(autonomous underwater vehicle,AUV)是水下机器人的一种,其在深海资源勘探开发、海洋水文观测、海洋测量等民用领域正起着重要作用,而且在军事领域有着广泛的应用前景,越来越受到各国的重视[1].目前,世界上有近10个国家的40多个部门在研究军用和民用AUV[2];在AUV的这些实际应用中,精确的位置跟踪控制通常是必需的[3-4].但出于成本和减重等的考虑,AUV横向和垂向大多没有推进器,受到不可积的二阶非完整约束,是欠驱动系统[5],这使得AUV的跟踪控制成为一个极具挑战性的问题.文献[4]针对欠驱动航行器,基于李雅普诺夫稳定性理论使用backstepping方法提出了一个位置跟踪控制策略,但没有考虑参数不确定性和外界干扰,而且其使用横向速度作为虚拟控制输入,提出的控制策略只能使位置跟踪误差收敛到一个很小的区域内.AUV是强非线性系统,很难获得其精确的水动力系数,易受到海流等外界干扰影响[6-7],这就需要控制器有较强的鲁棒性.
基于以上考虑,本文针对具有参数不确定性和外界干扰的欠驱动AUV,基于李雅普诺夫稳定性理论使用backstepping方法设计了一个平面位置跟踪控制器;为了提高控制系统的鲁棒性,引入滑模变结构控制策略;为了得到一个更加实用的控制器,用一个陡峭的饱和函数代替滑模控制器中的符号函数.最后将该控制器对具有参数不确定性和外界干扰的欠驱动AUV系统进行了数值仿真,结果表明本文设计的控制器能很好地实现欠驱动AUV的平面位置跟踪控制,有很强的鲁棒性,动态性能很好.
1 问题描述
AUV运动一般为空间6自由度,不过在弱机动性时可以被解耦为水平面与垂直面的平面运动.本文仅讨论水平面运动情况.欠驱动AUV的水平面运动学方程可表示为[8]

动力学方程可表示为[5,8]
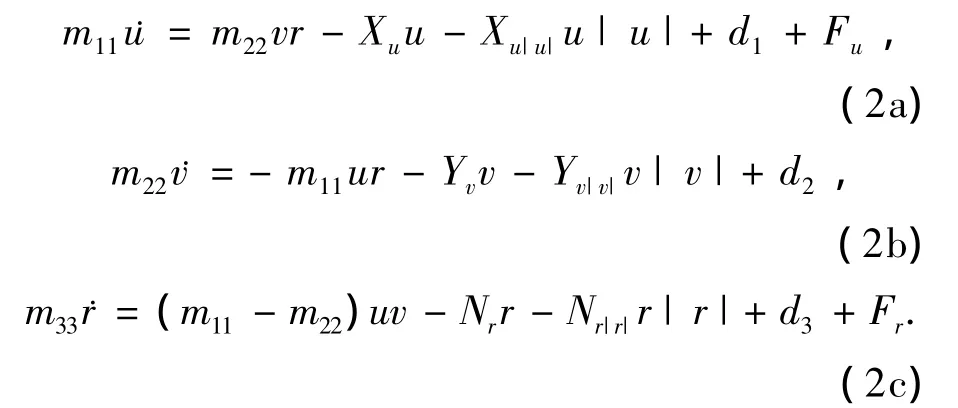
其中:m11=m-X˙u,m22=m-Y˙v,m33=Iz-N˙r.
方程(1)和(2)中的参数的物理意义请参见文献[5,8].从上述方程可看出,横向没有控制输入,是欠驱动系统.在实际应用中,参数m11,m22,m33,Xu,Xu|u|,Yv,Yv|v|,Nr和Nr|r|都是正值,Fu,Fr,u,r,˙u和˙r都是有界的.由于方程(2)中的系统参数的标称值并不足够精确,以P,P0和P*分别代表系统参数的实际值,标称值和摄动值,它们关系可表示为

则方程(2)可重写为
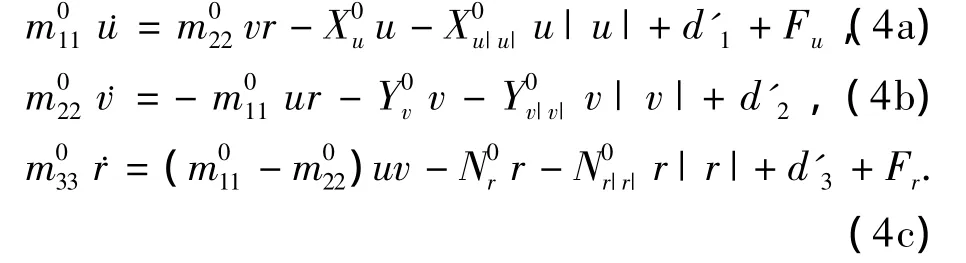
其中
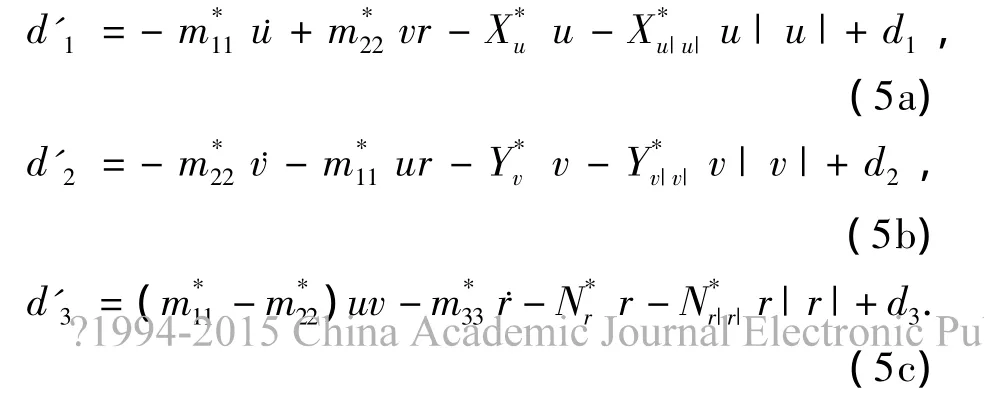
假设参数不确定性P*是有界的,且

其中-0.5<ζ<0.AUV在近水面主要受波浪干扰,在离水面较远处主要受海流干扰,这两者都较难精确建模[9].根据文献[6,10],外界干扰一般可取为以下形式
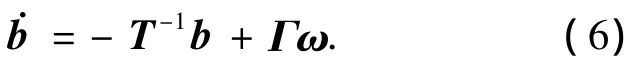
其中b=[b1b2b3]T代表干扰力和力矩向量; ω =[ω1,ω2,ω3]T∈R3代表平均值为零的高斯白噪声;T∈R3×3是一个正值对角矩阵;Γ∈R3×3是一个表征高斯白噪声幅值的对角矩阵.为了更好地分析有无外界干扰情况下的仿真结果,同时考虑到外界干扰都是有界的[6],本文的外界干扰d=[d1d2d3]T取为
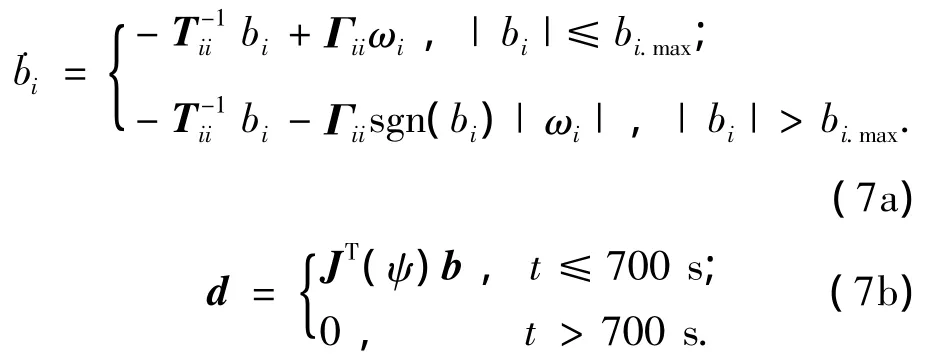
为了便于论述,定义
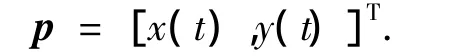
以pd=[xd(t),yd(t)]T:[0,∞)→R2代表一条足够光滑的时变的期望轨迹,且该期望轨迹的两阶导数有界.则本文研究的问题描述如下:针对方程(1)~(7)表示的欠驱动AUV系统,设计一个控制器使所有闭环信号有界且跟踪误差‖pdp‖快速收敛到零附近的一个可以任意减小的邻域.
2 鲁棒位置跟踪控制器设计
Backstepping是一种非常有效的非线性系统控制器设计方法,它通过逐步修正算法,设计镇定控制器实现系统的全局调节或跟踪,在每一步把状态坐标的变化、不确定参数的自适应调节函数和一个已知李雅普诺夫函数的虚拟控制系统的镇定函数等联系起来[11].
2.1 v的有界性
由于横向没有控制输入,所以很有必要先讨论下v的有界性.定义一个控制李雅普诺夫函数
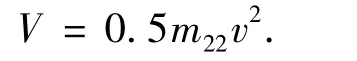
结合方程(2b),其导数为
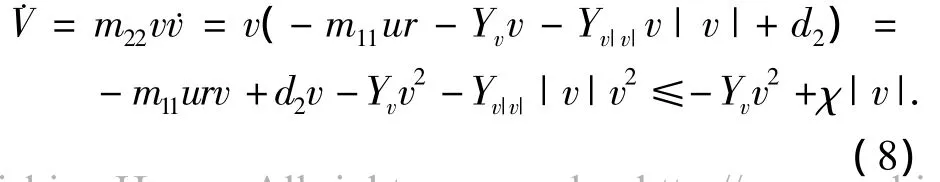
其中χ=max(|m11ur|+|d2|),方程(8)可重写为
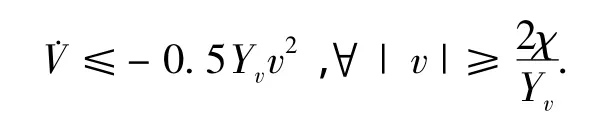
根据文献[12],方程(2b)代表的系统是输入状态稳定的,且
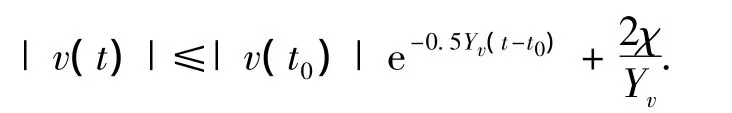
2.2 控制器设计
为了便于表达,定义
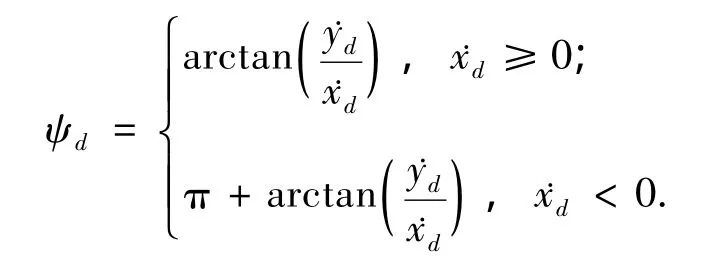
该角度取决于已知的期望位置xd和yd的变化率,完全不受模型不确定性的影响,通过定义ψe=ψd-ψ可以确定AUV相对参考轨迹的姿态.假设期望变量和都是有界的,ψe的初始值满足和cos ψe(t0)≥ε,其中ε是一个待定的正常数.
定义惯性坐标系位置跟踪误差为

则体坐标系下的跟踪误差可表示为
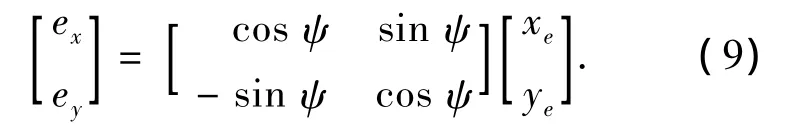
从方程(9)可得
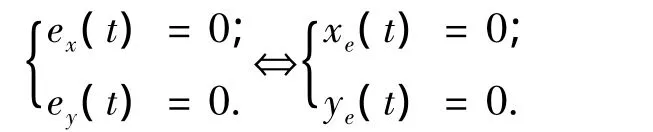
则只需设计控制律使跟踪误差ex和ey快速收敛到零附近的一个可以任意减小的邻域.根据方程(1)和(9),经计算可得ex和ey的导数为
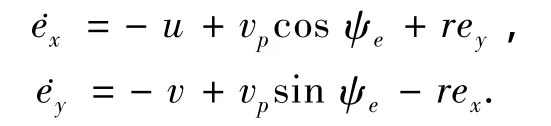
步骤1 镇定跟踪误差ex和ey.首先定义一个控制李雅普诺夫函数
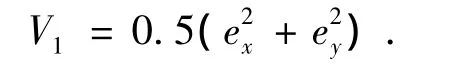
其导数为
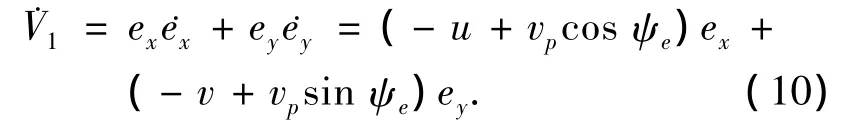
选择

为了使 ˙V1为负值,以u和α为虚拟控制输入,选择其期望值为
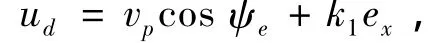

其中k1和k2都是正常数.为了确保存在ψe,使得vpsin ψe=v成立,假设vp满足将 ud和αd代入方程(10)可得
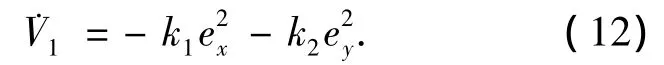
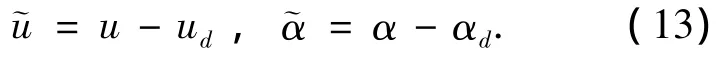
方程(12)变为
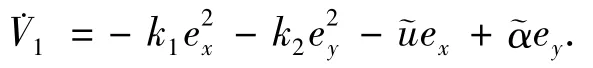
定义一个新的控制李雅普诺夫函数V2为
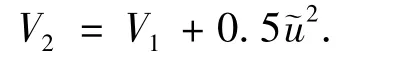
其导数为

选择控制输入Fu为
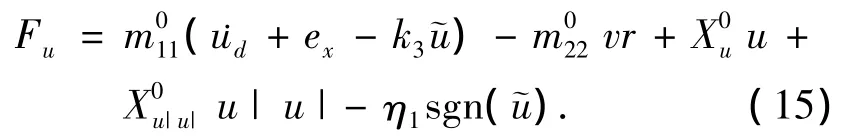

从方程(4a),(5a)和(15)计算可得
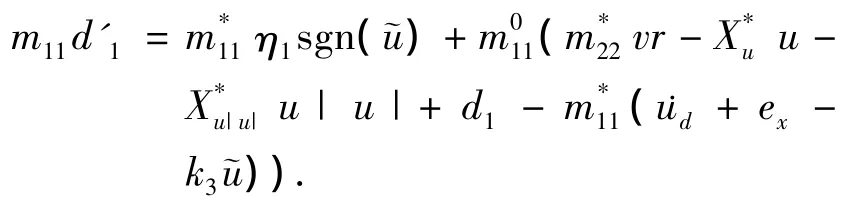
为了便于表述,定义
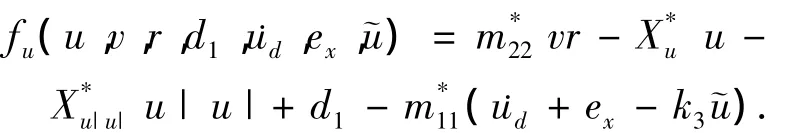
选择

则

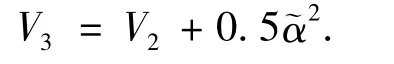
其导数为

经计算方程(11)和(13)可得

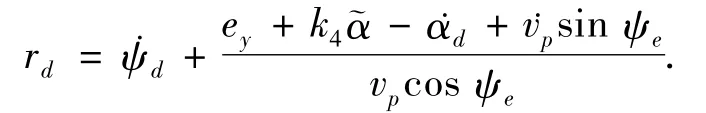
其中k4是一个正常数,方程(16)变为
近年来,网购盛行,但也存在产品真假难辨,出现产品质量问题维权难等引发购物风险的一系列问题。因此,企业建立有影响力的网络品牌有助于让消费者对产品产生信任,并通过保障产品质量和提供良好服务,促进产品的网络销售。
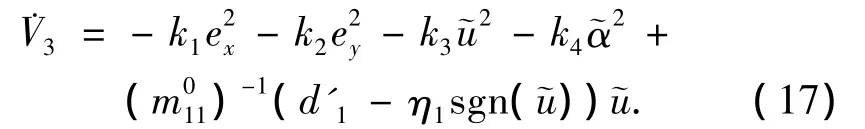
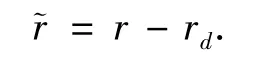
则方程(17)变为

定义一个新的控制李雅普诺夫函数V4为
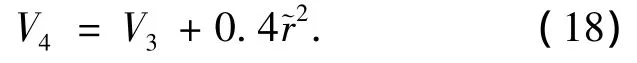
其导数为
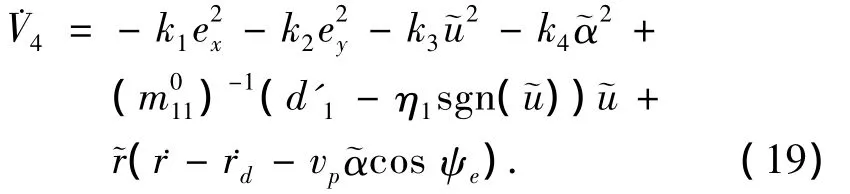
选择控制输入Fr为
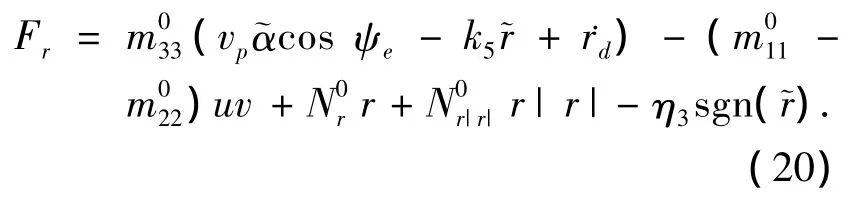
其中k5和η3为待定的正常数,方程(19)变为
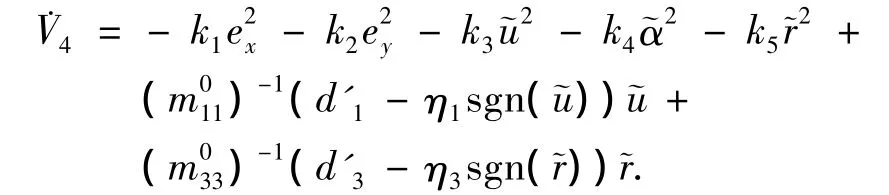
从方程(4c),(5c)和(20)计算可得

为了便于表述,定义
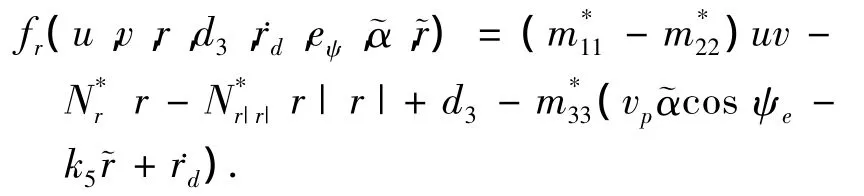
选择
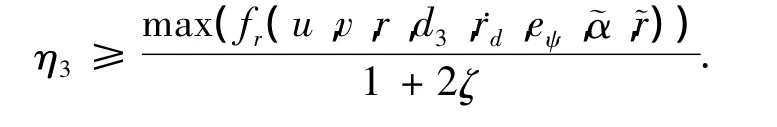
则
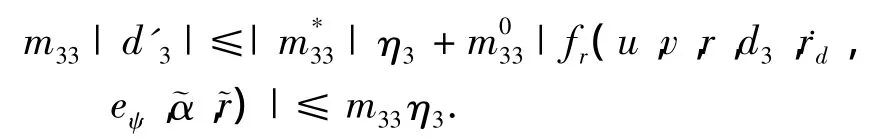
即|d'3|≤η3,则V4的导数满足
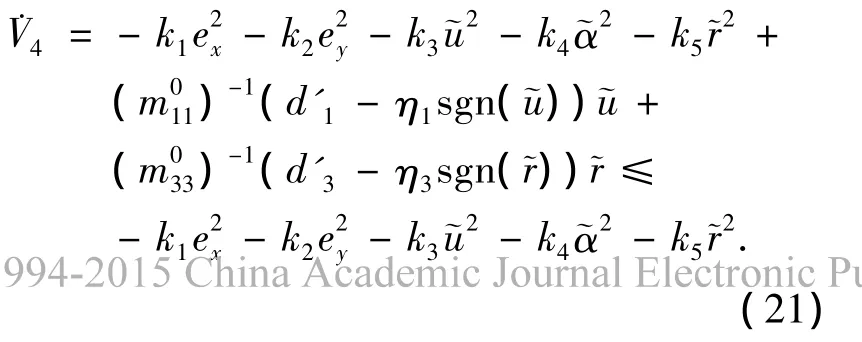
根据文献[12],最终的闭环系统是指数稳定的,位置跟踪误差将指数趋近到零.
2.3 关于控制输入Fr的讨论
需要特别注意的是,当cos ψe等于零的时候,rd将变成无穷大,控制输入Fr也变成无穷大而没有意义,所以有必要讨论下在使用本文提出的控制器且满足ψe的初始条件假设情况下,ψe的变化范围.
假设初始时刻为t0,考虑到和都是有界的,ψe的初始值满足和cos ψe(t0)≥ε,所以V4(t0)是有界的.根据文献[12]取γ=min{k1, k2, k3, k4, k5},由方程(21)可得
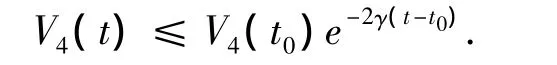
结合方程(18)可得
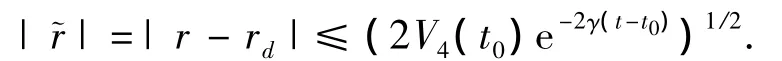
则|rd(t)|和|cos ψe(t)|满足

因此|rd(t)|和方程(20)中的控制输入Fr都是有界的.
2.4 一个实用控制器
在理论上,方程(15)和(20)的控制律能取得很好的控制性能,但该控制律的控制信号是不连续的,将产生抖振现象.在实际应用中,AUV系统是极其不希望出现抖振现象的.为了削弱抖振,根据文献[12],可用一个抖振的饱和函数来代替符号函数,则控制律可重写为
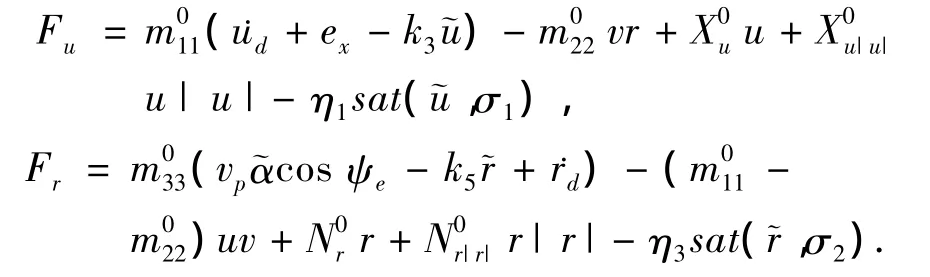
其中

其中σ1和σ2都是很小的正常数.根据文献[12],通过增大控制增益,或者减小σ1和σ2,该控制律能使跟踪误差收敛到零附近的一个可以任意减小的邻域,能够解决本文的位置跟踪问题.
3 数值仿真
根据文献[10,13],外界干扰系数为

AUV系统的标称参数参见文献[8],假设最大的参数不确定
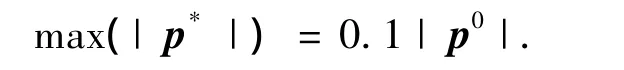
为了论证本文提出的控制器的鲁棒性,数值仿真包括以下3个仿真模型:1)标称参数且无外界干扰的标称模型;2)p*=-0.1p0且有外界干扰的不确定模型1;3)p*=0.1p0且有外界干扰的不确定模型2.期望轨迹为
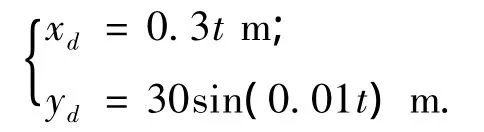
在AUV实际应用中,其控制输入都是受限的,为了更好地检验本文设计的控制器的性能,本文假设轴向推力是非负的,控制输入的幅值都受限,具体为
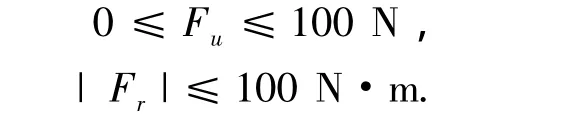
在接下来对所有仿真模型的所有数值仿真中,采用相同的控制器参数和初始条件,具体如下:控制器参数k1=10,k2=3,k3=k4=0.5, k5=0.1,σ1=σ2=1,η1=20,η3=20;初始值xe=1 m,ye=-1 m,ψ0=0,u0=0.01 m/s,v0=0,r0=0.
总的仿真时间为1 400 s,为了更好地观察相应变量的动态响应和稳态响应,xe,ye,ψe,Fu和Fr仿真结果分成1 400 s,前50 s和最后1 350 s三部分显示,具体仿真结果见图1~3.图1显示的是正弦期望轨迹和3个实际轨迹,从图中可以看到,对3个模型的仿真都有较好的宏观的跟踪性能;图2描述的是惯性坐标系下的跟踪误差xe和ye,可看出对于3个不同的仿真模型,跟踪误差都快速收敛到零附近的一个很小的邻域内;图3描述了控制力Fu和控制力矩Fr,从图中可看出,为了克服外界干扰的影响,控制力矩Fr变化较为剧烈,在无外界干扰时,Fu和Fr的响应曲线十分光滑.
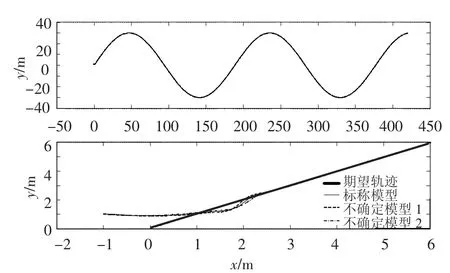
图1 正弦期望轨迹和实际轨迹
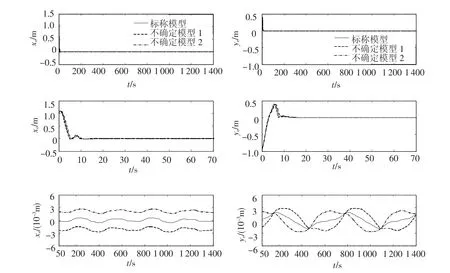
图2 位置跟踪误差xe和ye
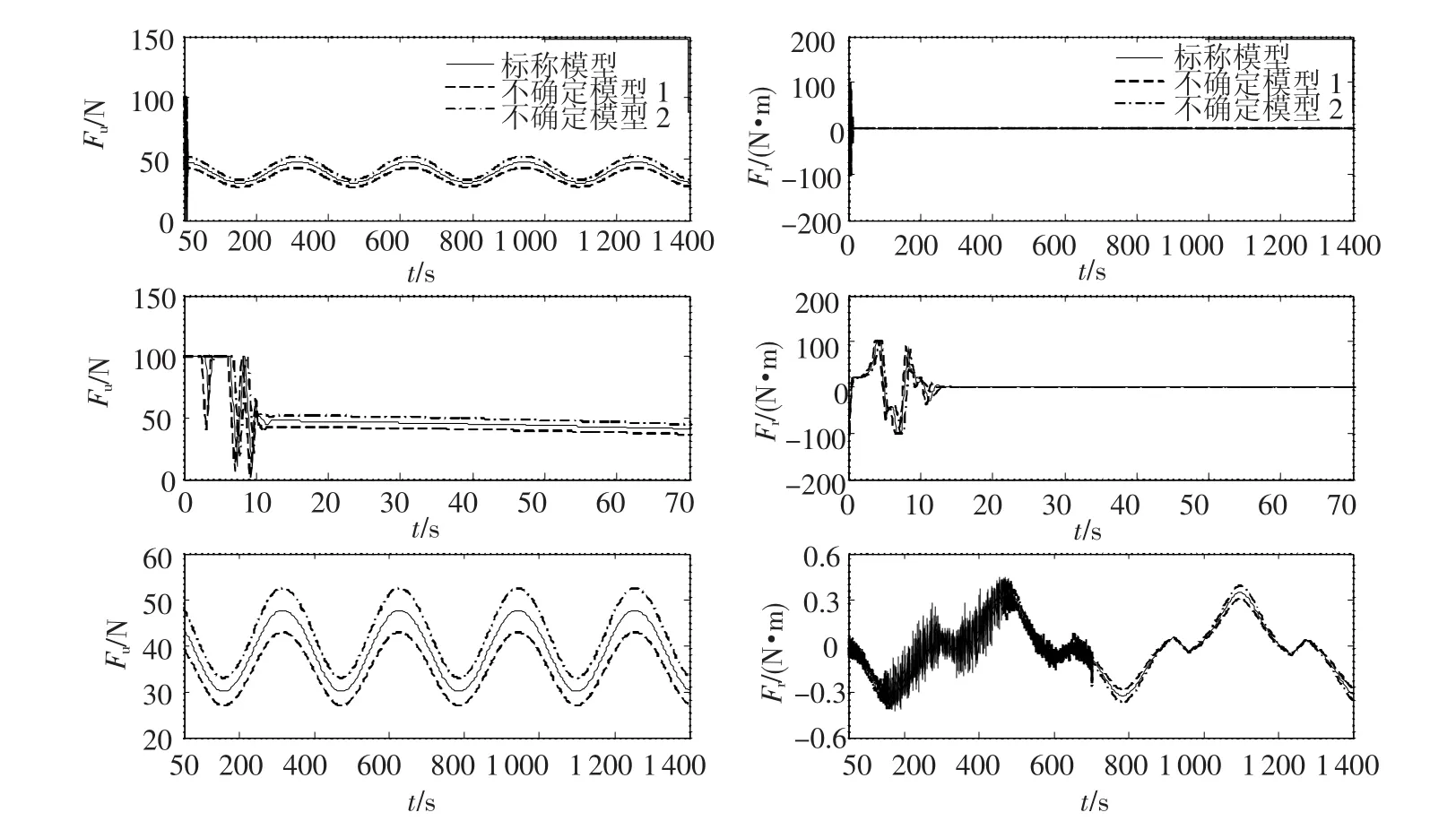
图3 控制力Fu和控制力矩Fr
4 结论
本文基于李雅普诺夫稳定性理论,使用反步法,结合滑模变结构控制方法,针对具有较大不确定性和强非线性动力学的欠驱动AUV设计了一个鲁棒平面位置跟踪控制器;对具有参数不确定性和外界环境干扰的欠驱动AUV系统进行了数值仿真,结果表明该控制器能很好地实现欠驱动AUV的水平面位置跟踪控制,具有很强的鲁棒性.
[1]BOVIO E,CECCHI D,BARALLI F.Autonomous underwater vehicles for scientific and naval operations[J].Annual Reviews in Control,2006,30(2):117-130.
[2]李涛,李晔.一种有效的水下机器人并行定位标图方法[J].哈尔滨工业大学学报,2008,40(5):818-822.
[3]STUTTER L,LIU H H,TILLMANC,et al.Navigation technologies for autonomous underwater vehicles[J].IEEE Transactions on Systems Man and Cybernetics-Part C:Applications and Reviews,2008,38(4):581-589.
[4]AGUIAR A P,HESPANHA J P.Position tracking of underactuated vehicles[C]//Proc of the Amer Control Conference.Denver,CO:[s.n.],2003:1988-1993.
[5]AGUIAR A P,PASCOAL A M.Dynamic positioning and way-point tracking of underactuated AUVs in the presence of ocean currents[J].International Journal of Control,2007,80(7):1092-1108.
[6]FOSSEN T I.Guidance and Control of Ocean vehicles[M].New York:Wikey,1994.
[7]NAIK M S,SINGH S N.State-dependent Riccati equation-based robust dive plane control of AUV with control constraints[J].Ocean Engineering,2007,34(11-12):1711-1723.
[8]REPOULIAS F,PAPADOPOULOS E.Planar trajectory planning and tracking control design for underactuated AUVs[J].Ocean Engineering,2007,34(11-12): 1650-1667.
[9]REFSNES J E,SIREBSEB A J,PETTERSEN K Y.Model-based output feedback control of slender-body underactuated AUVs:Theory and experiments[J].IEEE Transactions on Control Systems Technology,2008,16 (5):930-946.
[10]LORIA A,FOSSEN T I,PLANTELEY E.A separation principle for dynamic positioning of ships Theoretical and experimental results[J].IEEE Transactions on Control Systems Technology,2000,8(2):332-343.
[11]胡跃明.非线性控制系统理论与应用[M].北京:国防工业出版社,2005.
[12]KHALIL H K.Nonlinear Systems[M].3rded.Upper Saddle River,NJ:Prentice-Hall,2002.
[13]DO K D,PAN J,JIANG Z P.Robust and adaptive path following for underactuated autonomous underwater vehicles[J].Ocean Engineering,2004,31(16): 1967-1997.

