基于改进二维Ostu算法的SAR图像分割方法研究

韩志斌，林 涛，杨 坤，张 林

（1.海军航空工程学院 a.控制工程系；b.科研部；c.学员旅，山东 烟台 264001；2.91980 部队，山东 烟台 264001）

合成孔径雷达（SAR）具有全天候、全天时对地观察能力，利用实时获取的SAR 目标影像与飞行器中存储的光学参考影像匹配来辅助惯导，可以实现高精度的自主导航。SAR图像中含有丰富的地物信息，如果能从中分割出关键的地物，就可以利用关键地物的特征进行匹配，从而大大提高影像匹配的可靠性与效率。

阈值分割法实现简单、计算量小、性能较稳定，是一种最基本的图像分割技术。多数典型目标如道路、河流等在SAR图像上往往呈现暗性线体，与背景形成强烈的反差，因此这些目标非常适用于采用阈值法进行分割[1]。由日本学者大津[2]较早提出的一维Ostu 法，因其分割效果较好且速度快而成为有代表性的阈值分割方法。但由于一维直方图无法反映图像的局部空间信息，当应用于含有较多相干斑噪声的SAR图像时分割效果不佳。Abutaleb 和Brink[3-4]利用像素的灰度值和邻域平均灰度值两个特征，提出了二维直方图的概念。刘健庄等[5]提出了二维直方图上的Ostu方法，但该方法的目标和背景区域划分不准确，影响了分割效果；同时该方法将一维灰度阈值搜索空间拓展为二维，降低了分割速度。阳波[6]采用遗传算法对二维灰度阈值参数进行寻优，加快了分割速度。但遗传算法容易陷入局部最优，稳定性较差，且不利于硬件实现。

针对基于二维直方图的Ostu 法的缺陷，本设计将目标与背景区间进行重新划分，并提出了一种新的最大类间方差计算方法对原方法加以改进。

1 二维Ostu方法原理

对于一幅M× N大小的灰度图像，设f(x,y)为图像在(x,y)点的灰度值，g(x,y)为以(x,y)为中心的k× k邻域内的平均灰度值，其灰度级均为L。定义二维直方图N(i,j)的值表示为像素灰度值f(x,y)=i 且同时像素邻域平均灰度值 g(x,y)=j的像素的个数。基于像素灰度和像素邻域灰度均值，绘制二维直方图如图1所示。

图1 基于像素灰度和邻域灰度均值的二维直方图

定义了二维直方图后，可以利用像素点的灰度值和其邻域平均灰度值组成的二元组(i,j)来表示图像。若设二元组(i,j)出现的频数为fij，则相应的联合概率密度 pij为：

pij与 fij成正比，二者在三维坐标系中的分布趋势相同。根据同态性，在目标和背景处，像素的灰度值和邻域的平均灰度值接近，在目标和背景的分界邻域或噪声点处，像素的灰度值和邻域的平均灰度值差距较大，因此目标和背景中的像素将出现在对角线周围。所以图2中，pij分布主要集中在(0,0)～(L − 1,L−1)对角线周围。令二维矢量(s,t)为阈值，可将图像的二维直方图分成4个区域，区域 C0代表目标，区域 C1代表背景，远离对角线的A 和B代表可能的边缘和噪声[7]。

图2 二维直方图阈值分割示意图

二维Ostu方法只计算区域 C0和区域1C的类间方差而忽略含噪声较多的A 和B 区域，可以尽量减少噪声的污染，取得相对一维Ostu方法更好的分割效果。

其具体原理为[8]：利用二维直方图中任意门限向量(s,t) 对图像进行分割，那么区域 C0和区域1C发生的概率分布为：

背景和目标的均值矢量分别为：

由于远离直方图对角线二元组的概率可忽略不计，则 w0+w1≈1，总体均值 µz可表示为：

定义 C0与1C类的类间方差为：

由式(7)可知，类间方差S为阈值(s,t)的函数。对阈值(s,t)进行遍历搜索，当S 取得极大值时，得到的值(s0,t0)即为最佳分割门限。

在确定了分割门限后，定义：

从而完成了图像分割。

2 改进的二维Ostu方法

2.1 二维Ostu方法的缺陷

二维Ostu方法（阈值为(s,t)）在计算类间方差时，假设噪声或图像边缘全部在A、B区域，而目标和背景的内部区域全部在 C0、C1上。实际中目标和背景的内部区域如图3中的黑点所示，可见，该法的假设忽略了A、B 区域中的目标和背景的内部元素，同时考虑了C0、C1部分中远离对角线的部分边缘像素及噪声的值，造成了阈值选取时的误差[9]。

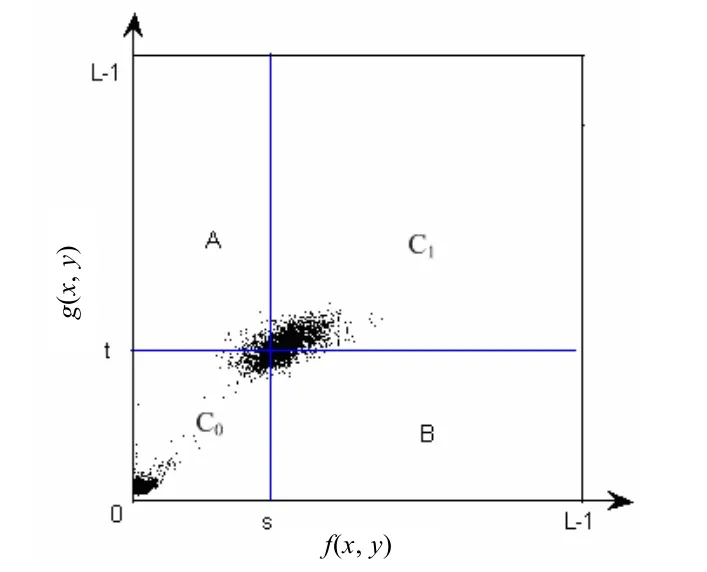
图3 二维Ostu方法误差示意图

此外，二维Ostu方法虽然分割效果优于一维Ostu方法，但由于二维直方图的引入，每个阈值的类间方差计算复杂度相对提高，且阈值的搜索空间由一维变为二维，大大增加了算法的运行时间，导致该算法难以应用于实时性要求较高的SAR图像匹配导航系统。

2.2 二维Ostu方法的改进方案

基于以上分析，对二维Ostu方法做如下改进：定义松弛变量m、n，假设图像内部像素位于g(x,y)=f (x,y)+n与g(x,y)=f (x,y)−m 之间的区域（m、n为某一固定常数），如图4所示。

图4 改进的二维Ostu方法区域分割示意图

当阈值为s时，直线 f(x,y)=s 将该区域分成C0、C1两部分，用其来代替图3中的C0、C1。

此时，区域 C0的概率分布为：

式中：

pi,j为联合概率密度；

m、n为松弛变量。

区域 C1发生的概率分布为

式中，w0(L−1)为区域 C0与区域 C1的总概率。

令：

则目标和背景的均值矢量分别为：

目标和背景的类间方差为：

最优阈值s*为：

分割后的图像ft(x,y)为：

在每一步类间方差的计算中，可根据上一步的结果分别对 w0(s)、P0(s)进行迭代运算，以减少计算量。迭代过程为：

2.3 松弛变量的选择

由图4中的区域划分方法可知，松弛变量m、n 决定了计算类间方差时所用的区域大小。若m、n过小，则区域 C0与 C1不能覆盖全部的目标与背景内部区域，导致类间方差计算不准确而影响分割效果。其值过大，区域中又会掺入噪声点（图5）。因此，如何选取合适的m、n值成为影响分割准确度的一个关键问题。

对于图4的区域划分方法，分别计算在不同 ∆d下直线 g(x,y)=f (x,y)+∆d 上所有点在二维直方图（图2）中的N(x,y)的平均值。

由于N(x,y)分布主要集中在(0,0)～ (L− 1,L−1)的对角线周围，因此，在∆d=0处，最大，且随着 ∆d的增大，逐渐减小且下降较快。当 ∆d 较大时，直线上的点均为边缘或噪声点，因此，趋于平缓，当 ∆d很大时，直线g(x,y)=f (x,y)+∆d的长度已很短，此时，变为0。

图5 松弛变量取值对分割效果的影响

图6 N (x,y)分布与松弛变量取值示意图

3 实验结果

在Matlab 平台下，分别运用一维Ostu方法、二维Ostu方法以及本文改进的二维Ostu方法对SAR 河流实时图进行分割，结果如图7所示。

图7 SAR 河流图像各种方法分割结果比较

从目视效果看，一维的Ostu方法对目标的分割效果较差，背景区域含有大量干扰，目标与背景混淆在一起；二维Ostu方法在一定程度上抑制了干扰，但效果仍不理想；相比于二维Ostu方法，改进二维Ostu方法很好地去除了背景干扰，目标较为清晰。

从各种方法的运行时间上进行比较，通过表1可以看出，二维Ostu方法虽然分割效果好于一维Ostu方法，但因为运行时间长，并不适用于实时性要求较高的SAR 导航图像匹配。通过对二维Ostu方法的改进，使其运行时间仅为0.3 s 左右，大大增加了该方法的实时性。为验证本文算法的适用范围，用本文算法分别对机场、岛屿等与背景对比度明显的目标进行分割，均取得了良好的效果。

表1 各种方法的运行时间比较

4 结论

针对INS/SAR组合导航系统中的合成孔径雷达图像分割问题，本文在二维Ostu方法的基础上对区域划分进行了改进，并通过引进松弛变量减少了阈值搜索维数。仿真结果证明：对于机场、岛屿、河流等与背景对比度明显的目标，该方法均可取得较好的效果且具有很强的抗噪性与实时性，满足了INS/SAR 导航系统的要求。

[1]宋建社,郑永安,袁礼海.合成孔径雷达图像理解与应用[M].北京:科学出版社,2008:57-60.

[2]OTSU N.A threshold selection method from gray-level histogram[J].IEEE trans System Man Cybernetic.1979,9(1):62-66.

[3]ABUTALEB A S.Automatic thresholding of gray-level pictures using two-dimensional entropy[J].Computer Vision,Graphics Image Processing,1989,47:22-32.

[4]BRINK A D.Thresholding digital images using two-dimensional entropy[J].Pattern Recognition,1992,25(8):803-808.

[5]刘健庄,栗文清.灰度图像的二维Ostu 自动阈值分割法[J].自动化学报,1993,19(1):101-105.

[6]阳波.基于最大类间方差遗传算法的图像分割方法[J].湖南师范大学自然科学学报,2003,26(1):32-36.

[7]李弼程,柳葆芳.基于二维直方图的模糊门限分割方法[J].数据采集与处理,2000,15(3):324-328.

[8]冯斌,王璋,孙俊.基于量子粒子群算法的Ostu图像阈值分割[J].计算机工程与设计,2008,29(13):3429-3434.

[9]杨金龙,张光南,厉树忠,等.基于二维直方图的图像分割算法研究[J].激光与红外,2008,38(4):400-403.