正六角形蜂窝芯层面内等效弹性参数研究

陈梦成，陈玳珩

(1.华东交通大学土木建筑学院，江西南昌330013;2.日本东京理科大学机械工学科，东京162-8601)

近年来，蜂窝材料作为一种轻量化与高强化高性能先进复合材料在机械和土木结构中得到广泛应用，如何准确确定其等效弹性参数亦备受关注。早期在分析由周期性胞元构成的蜂窝材芯层强度时，通常假想地将其视为一块均质各向异性薄板，并通过一系列弹性参数和结构特征胞元的变形满足宏观本构方程来描述其宏观等效的力学弹性参数。关于等效弹性参数的理论分析，到目前为止，已有不少报道[1-5]。但是，在这些研究结果中，均忽略了胞元壁板剪切变形的影响。实际上，当蜂窝芯层较厚的时候，这种剪切变形不能忽略。在胞元壁板考虑剪切变形的情况下，本文拟就由图1(a)所示的正六角形胞元周期性排列组成的图1(b)中正六角形蜂窝芯层的面内等效弹性参数进行理论分析。

1 考虑剪切变形的面内等效弹性参数理论分析

结构的变形和失稳问题可以通过分析与母体力学结构相似的结构特征单元在相同载荷下的变形和失稳现象得到比较简单而又直接的解决。整个蜂窝状夹芯层面内变形的求解可以通过分析图1(b)中点线范围内所示的单个代表性特征单元变形而获得，本节拟开展这方面工作。图2(a)为从图1(b)中点线范围内割出的单个单元示意图，图2(b)为蜂窝夹芯层受均匀拉伸作用时构成单个单元的胞元壁ABB′A′、CBB′C′和DBB′D′在连接处所受的力和弯矩示意图，图中采用局部坐标系(ξ，η，ζ)。整体坐标系(x，y)平面和局部坐标系(ξ，ζ)平面均置于胞元壁高半中腰位置。z坐标轴与η坐标轴重合，即z=η。胞元正壁和胞元斜壁的物理量分别用下标v和l加以区分。另外，为了区别整体坐标系下隔蜂窝状结构等效应力与局部坐标系下胞元各壁板应力，整体坐标系下应力符号上方使用符号～。

图1 蜂窝芯层结构

图2 结构特征单元及其受力分析

首先来确定蜂窝芯层在x方向的材料性质。为此，假定蜂窝芯层在无限远处受到x方向的均匀拉伸载荷作用，则作用在胞元正壁板的分布力为

作用在胞元斜壁上沿x方向和y方向的分布力px|l(η)与py|l(η)分别为

它们沿ξ方向(斜壁面内)和ζ方向(斜壁面外垂直)的分解力为

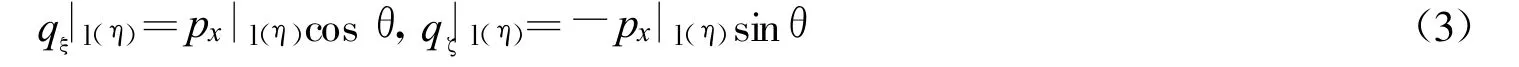
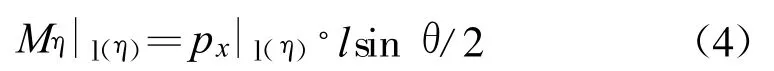
下面讨论图3中单元内各个壁板沿x方向的变形δix和y方向的变形δiy的求解方法，它们分别是单元内各壁板变形在x方向和y方向投影代数和。图3中粗线代表胞元壁，细线方框内表示的是分析单元的区域。胞元壁板的变形是在px|l(η)作用下，由力q|

ζl(η)引起的弯曲变形和剪切变形以及由力q|ξl(η)引起的伸缩变形共同形成的。

胞元正壁板由于没有受到力的作用，所以其变形等于零，即

图3 单元内各胞元壁板变形投影叠加示意图

它们在x方向和y方向的投影自然也就为零。

对于胞元斜壁板来说，由于载荷和结构对称，所以只需要分析其中一块斜壁板变形。胞元斜壁板一共受三种载荷作用，它们是弯矩Mη|l(η)、轴向力qξ|l(η)和剪力qζ|l(η)。因此，由材料力学知识，我们可以得到Mη|l(η)引起的胞元斜壁板弯曲变形挠度为

式中:Iξ=ht3/12;h为蜂窝芯层高度或胞元壁板宽度;l为胞元壁板长度;t为胞元壁板厚度;Es为胞元壁板纵向弹性模量。在x方向和y方向投影|x和|y分别是

剪力qζl(η)引起的胞元斜壁板弯曲变形挠度为

剪力qζ|l(η)引起的胞元斜壁板剪切变形挠度为

式中:A为受剪截面面积;k是关于剪切变形的修正系数。本文为了研究方便，取k=1(Mind lin[6]研究中取k=π2/12;Reissner[7]研究中取k=5/6)。在x方向和y方向投影|x和|y分别是

伸缩力qξ|l(η)引起的胞元斜壁板伸缩变形为

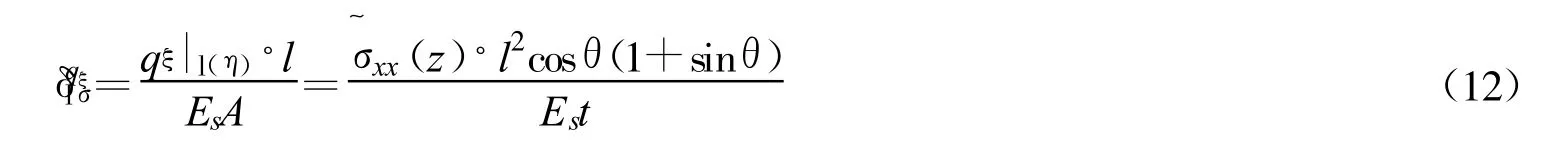
综上所述，单个单元在x方向产生的总变形为

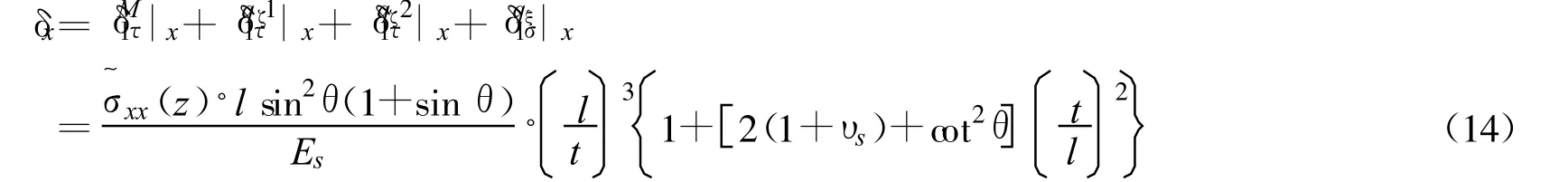
相应地，单个单元在x方向产生的线应变为

单个单元在y方向产生的总变形为

相应地，单个单元在y方向产生的线应变为

根据Hooke定律，蜂窝芯层在x方向的等效弹性模量为

等效Poisson比υxy由定义得

同理，可以得到y方向的等效弹性模量

和等效Poisson比

以上式(18)-(21)即为蜂窝芯层面内等效弹性参数新结果，它们分别可以退化到Gibson和Ashby公式[4]和宋明慧公式[5]。比较式(18)-(21)，蜂窝芯层材具有各向异性。面内参数，还包含另一个剪切模量参数μxy，限于篇幅，我们拟在另文中报道。

2 结论

本文严格从材料力学出发，导出了蜂窝芯层面内等效弹性参数的理论分析公式。该公式考虑了胞元壁板各种变形产生的影响，克服了过去公式不全面的弱点。

[1] GIBSON L J，ASHBYM F，SCHAJERGS，ROBERTSTONC I.Themechanicsof two-dimensional cellularmaterials[J].Proc Roy Soc，1982，A382:25-42.

[2] MASTERS IG，EVANSK E.Models for the elastic deformation of honeycombs[J].Compos Struct，1996，35(4):403-422.

[3] WARRENW E，KRAYNIK AM.The linear elastic response of two-dimensional spatially periodic cellularmaterials[J].Mech Mater，1987，6(1):27-37.

[4] GIBSON L J，ASHBYMF.Cellular Solids:Structures&Properties[M].Oxford:Pergamon Press，1988:89-93.

[5] 富明慧，伊久仁.蜂窝芯层的等效弹性参数[J].力学学报，1999，31(1):113-118.

[6] MINDLIN RD.Influenceofrotatory inertiaand shear on flextualmotionof isotropic p lates[J].ASME JApp lMech，1951，18(1):31-38.

[7] REISSNERE.The effectof transverse shear deformation on the bending of elastic plates[J].ASME JApplMech，1945，12(1):69-77.