“中三角”经济圈“区域经济—交通运输”复合系统分析

王爱和,漆 昕,钟茂生

(华东交通大学交通运输与经济研究所,江西南昌330013)

武汉、长沙、南昌经济圈,简称为“中三角”经济圈,是指以武汉、长沙、南昌3个已经形成的中心城市为核心,以浙赣线、长江中游交通走廊为主轴,囊括大武汉城市群、泛长株潭城市群、大南昌城市群在内的所有城市及沿长江沿浙赣铁路线的所有城市,所形成的经济圈。构建以武汉、长沙、南昌3个中心城市作为支撑的“中三角”经济圈,对于带动整个长江中游的经济发展十分有利,对促进中部经济、长江带经济乃至全国经济的发展具有重要的战略意义。

由于区域经济与交通运输之间有很强的关联性,为了构建“中三角”区域经济圈,必须分析和评价经济圈内区域经济与交通运输的协调性,计算“中三角”经济圈经济与交通的关联度,并从综合运输的角度,制定未来一定时期的交通发展战略,以及在交通设施规划、建设和管理中应采取的措施,以满足地区经济发展需要,实现生产力布局与交通运输布局的合理结合,加快地方经济的发展。

关于交通运输与区域经济发展与协调性的评价模型问题,许多专家学者做了大量的研究工作:汤兵勇等人基于专家评分法提出了协调发展指数模型[1];汪传旭将协调发展指数模型应用到交通运输与经济的协调发展评价上,也将灰色系统协调模型用于判断交通运输与经济之间的协调关系,计算协调发展系数[2];武旭等人建立了一套反映经济系统和交通运输系统的指标体系,并分别作为输入和输出,用DEA(数据包络分析)研究了铁路运输以及整个交通运输业与社会经济的协调发展评价问题以及交通运输与经济的协调发展评价[3-4];在系统协调性评价上,杜志平等人构建了基于DEA的评价流程[5];曾珍香构建了基于系统论的可持续发展的系统协调性指数[6]。

本文基于以上成果,改进地使用“交通运输—区域经济”复合系统的效率评价模型[7],利用DEA交叉分析方法,来分析“中三角”经济圈交通运输与经济的关系。下面详细介绍复合系统效率评价模型、评价指标体系和“中三角”经济圈“交通运输—区域经济”复合系统分析过程与结论。

1 模型选择及指标体系建立

1.1 模型选择与描述

通常,为进行准确和有效的评价,综合评价模型应该能:(1)计算被评价对象的综合评价值;(2)能对被评价对象进行准确排序;(3)能对被评价对象进行正确分类;(4)能对被评价对象的现状给出改进建议。统计分析方法,如主成分分析、因子分析等,只能给出综合评价价值从而进行排序,聚类分析、判别分析只能满足第三个要求,层次分析在分析过程中很关键的一步是要构造判断矩阵,常常要用德尔菲法等定性方法,而近年来兴起的神经网络分析在网络学习和训练中要基于已有的研究成果,因而其使用也受到一定限制。应用于协调程度和可持续发展的评价方法,主要集中在专家评价法、技术经济评价法、多目标决策法以及层次分析法等。这些方法主要是对方案进行静态评价,能够进行时序性评价的较少。考虑到上述评价方法的缺陷以及对进行系统效率评价的要求,本文选用数据包络分析法(DEA)为评价模型。

常用的DEA模型的分式规划形式为

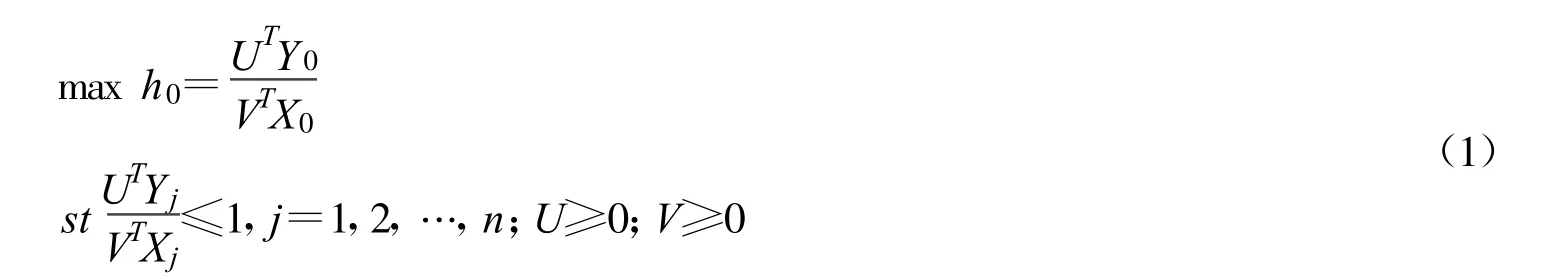
对该规划进行Charnes-Cooper线性变换和对偶变换后的形式为

式中:Xj=(x1j,x2j,…,xkj),j=1,2,…,n,xij为第j个DMU(Decision Making Unit)的第 i(i=1,2,…,k)种投入量;Yj=(y1j,y2j,…,ylj),j=1,2,…,n,yij为第j个 DMU的第 i(i=1,2,…,k)种产出量;(X0,Y0)为被评价对象;λj(j=1,2,…,n)为第 n个DMU的某种组合权重;为松弛变量向量。

若某个DMU的DEA模型的目标函数值为1,则称之为DEA有效,否则称之为非有效。然而,C2R模型只适合于用“点时刻”的输入、输出数据分析各个DMU在特定“点时刻”的状态。对于实际中常用的时间序列,随时间变化,生产前沿也会发生变化,因此,直接将时间序列数据用于C2R模型,会产生错误结论。据此,谢艾国等提出了时间序列DEA模型[8]。

设共有n个DMU,它们在第t(t=1,2,…,T)时段的输入指标为矩阵X(t),输出指标为矩阵Y(t),即

式中:x(t)ij为第j个DMU在第t时段内的第i种输入;y(t)kj为第j个DMU在第t时段内的第k种输出。要对各个DMU进行效率评价,先用模型(2)计算DMUk在各个时段的相对效率值,即

式中:e=(1,1,…,1)m,S为松弛变量,它代表各个DMU的效率与最优效率前沿面之间的距离,根据S的大小可进行动态综合效率排序。η0为S的和,称为动态综合效率评价指数,η0为0表示该DMU在动态生产前沿面上。η0越大,DMU的动态综合效率越小;η0越小,DMU的动态综合效率越大。

1.2 指标体系建立

DEA输入输出项选择的要求:第一,对所有决策单元,可以得到每个输入和输出值,而这些数值须为正数;第二,这些项目(输入、输出和DMU)的选择必须反映分析者对与决策单元的相对有效性评估相关的元素的兴趣;第三,从效率比的原则上考虑,输入的数值应该越小越好,而输出的数值应该越大越好。同时考虑到样本量的大小,指标不宜过多。

基于上述原因,本文建立的指标体系中的投入指标为:反映“交通运输—区域经济”复合系统资金输入的指标—固定资产投资,反映复合系统人力投入的指标—从业人数;输出指标为:反映区域经济产出规模的指标—国民生产总值(GDP),反映区域交通运输成果的指标—货运周转量和客运周转量。

2 “中三角”经济圈“区域经济-交通运输”复合系统分析

2.1 数据准备

本文指标数据来自于各省、地市历年统计公报及年鉴。由于DEA评价的是相对效率,其结论与样本选择有关,为得到较为客观的结论,本文选择近五年来(2004—2008)的数据。包括南昌、武汉、长沙历年固定资产投资、从业人数、GDP、货运周转量、客运周转量数据,详见表1。

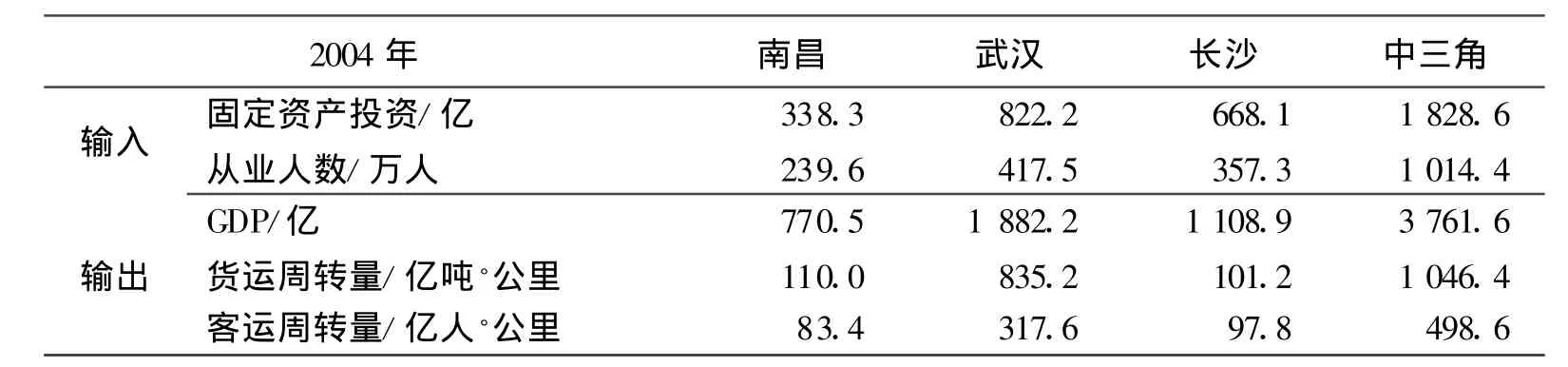
表1 “中三角”相对效率评价输入输出数据

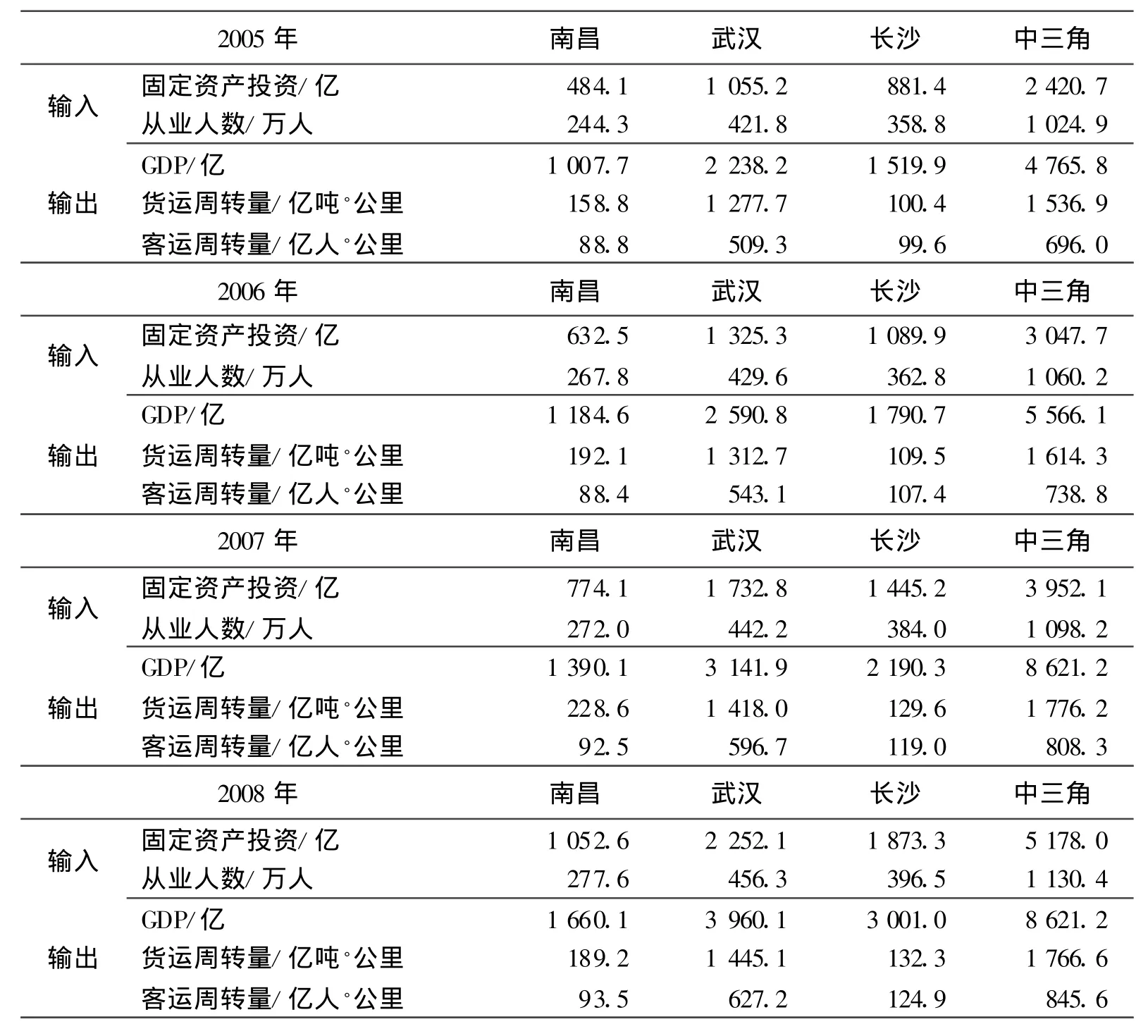
续表1

2.2 “中三角”交通运输与经济相对效率计算

本文改进地使用“交通运输—区域经济”复合系统的效率评价模型,利用DEA交叉分析方法,来分析“中三角”交通运输与经济的关系。经Matlab7.1编程实现评价模型,输入上述数据得出相对效率交叉评价矩阵,如表2所示。(注:各城市平均交叉评价值根据各城市之间交叉评价值得出,与中三角总值无关)

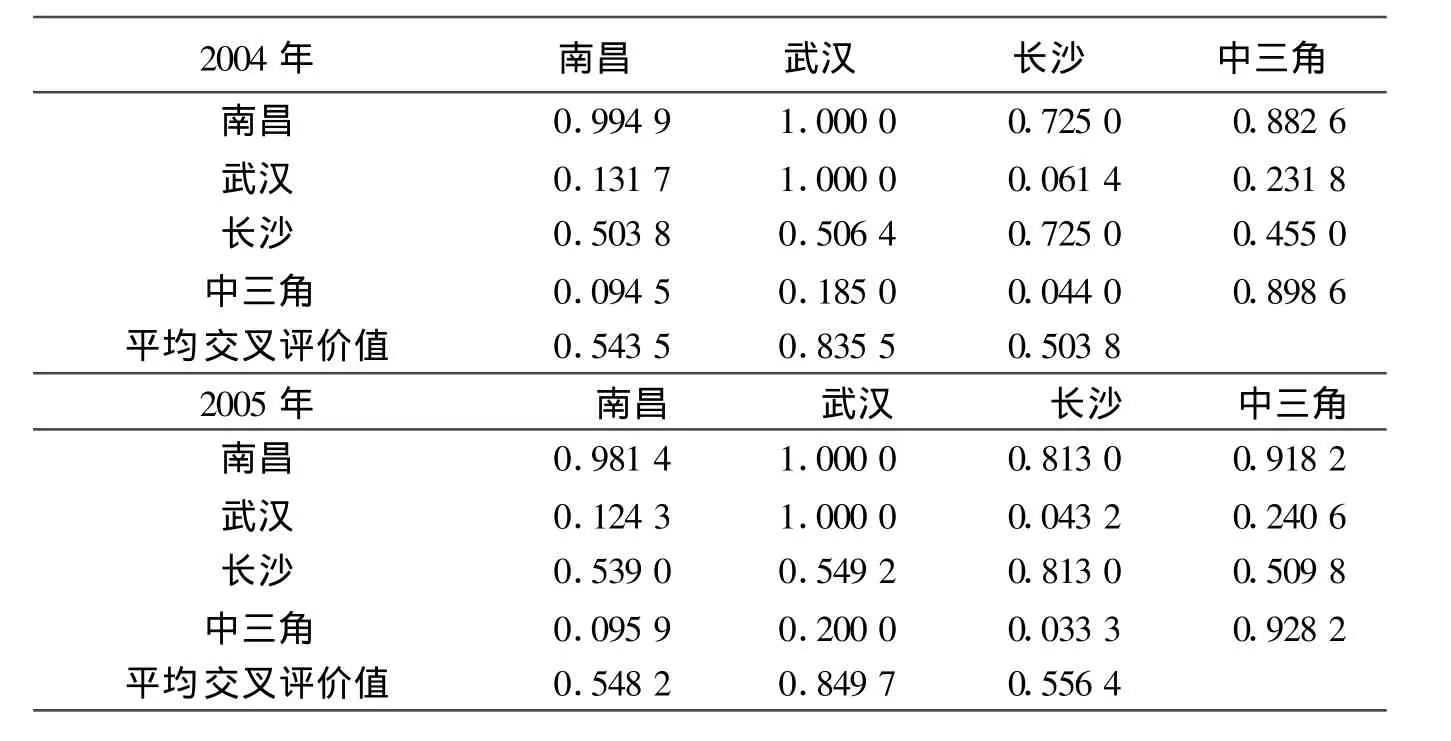
表2 “中三角”相对效率交叉评价矩阵

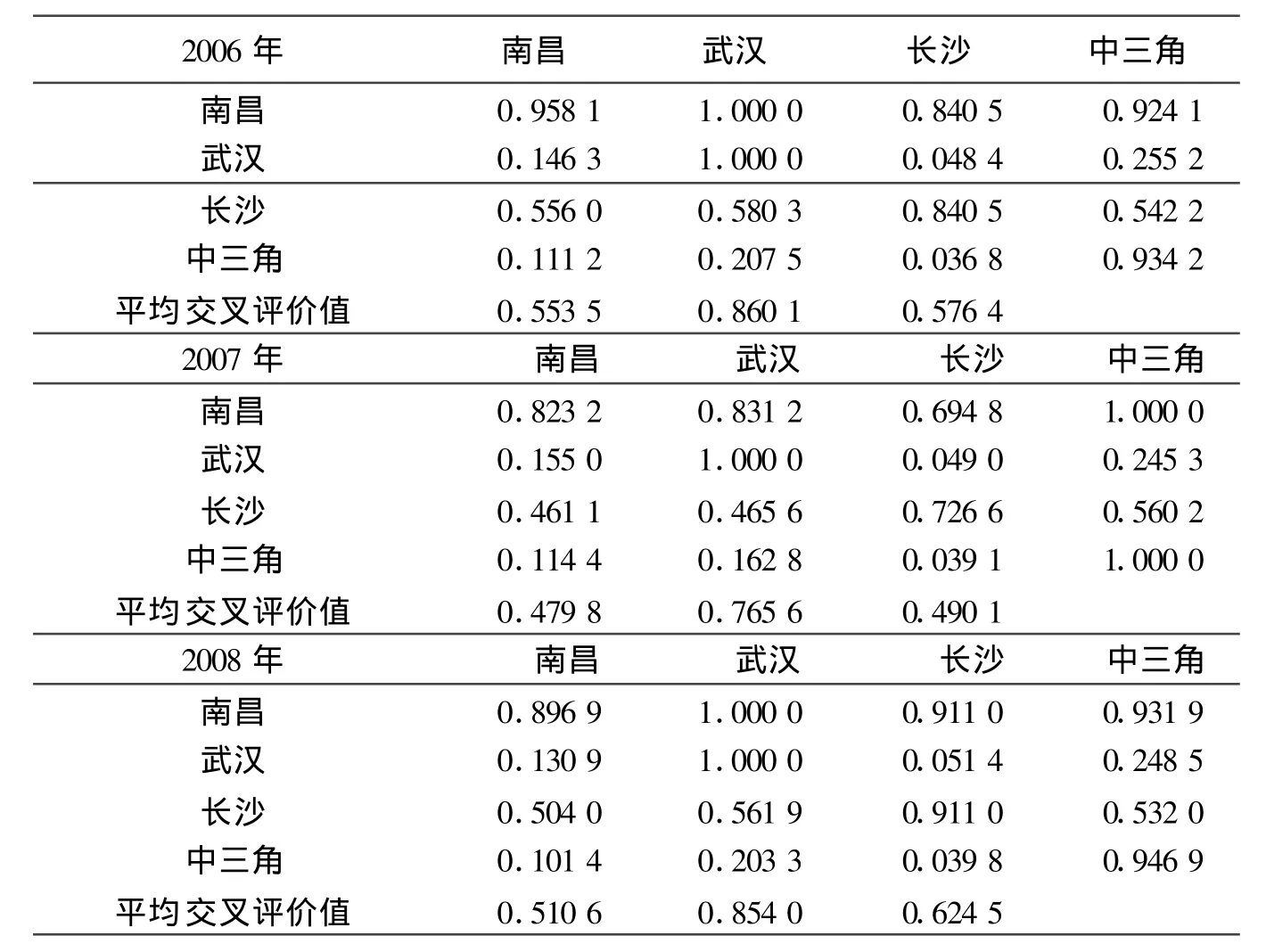
续表2

2.3 “中三角”交通运输经济协调性分析

从表1的数据可以看出:

(1)南昌固定资产投资和从业人口增长最快,其次为长沙、武汉;

(2)长沙GDP增长最快,其次为南昌、武汉;

(3)货运周转量武汉增长最快,其次为南昌、长沙;

(4)客运周转量武汉增长最快,其次为长沙、南昌。

根据计算结果(表2)可见,在2004—2008五年间:

(1)历年各城市自我评价值最高的为武汉。2008年之前南昌该值领先于长沙,但下降较快,2008年长沙反超南昌。“中三角”整体自我评价水平较高;

(2)南昌近两年来平均交叉评价值有下降趋势,长沙虽略有波动,但上升较快,已高于南昌,武汉则维持在一个较高的水平;

(3)南昌相对“中三角”各城市评价值均最底,长沙次之。“中三角”诸城市相对南昌的评价值最高,其次为长沙。

由此看见,“中三角”区域交通运输与区域经济发展协调性最好的是武汉,南昌下降的比较厉害,长沙上升较快,近年已赶超南昌;“中三角”区域整体交通运输与区域经济发展协调性水平呈上趋势,但2007年略有波动。

通过数据分析对比可知:

(1)南昌固定资产投资力度比较大、从业人员增长也比较快,整个国民经济的投入指标增长在3个城市之中是最快的,但是产出指标增长却并不让人非常满意,区域交通运输与区域经济发展协调水平也不尽人意。分析其原因,除基础薄弱,国民经济的投入指标效率不高之外,交通运输投入不足,交通运输网络架构薄弱造成经济与交通运输协调性水平不高也是个重要的原因。尤其是货运周转量虽高于长沙,但主要是因为京九铁路货运分流功能带来的过境运输,其公路、水运、航空货运周转量都远小于武汉、长沙。

(2)长沙近年来国民经济投入指标增长较快,虽略低于南昌,但由于其效率提升较快,产出指标GDP是3个城市之中增速最快的。经济与交通运输协调性水平虽低于基础较好的武汉,但近年来已经超过南昌。

(3)武汉在3个城市之中虽然国民经济投入指标增长最慢,但由于其基础较好,地理位置优越,其经济与交通运输协调性水平还是最高的。但是其GDP增长相比其他两个城市已出现颓势。

3 结束语

本文从“交通运输—区域经济”复合系统的角度出发,运用时间序列DEA分析方法,对“中三角”经济圈“交通运输—区域经济”复合系统运行动态综合效率进行了分析。结果显示,在“中三角”3个核心城市中:武汉的经济与交通运输协调性水平是最高的;长沙的经济与交通运输协调性水平虽低于基础较好的武汉,但近年来已经超过南昌;南昌的区域交通运输与区域经济发展协调水平有待提升。从构建“中三角”经济圈的全局战略考虑,“中三角”必须将交通运输建设与整个区域的社会经济发展结合起来,以交通运输网络建设引导城镇体系和生产力布局调整,形成规模效益,同时充分发挥各种运输方式的综合优势,构建现代化综合交通运输体系。

[1]汤兵勇,张文渊.协调发展指数模型[J].系统工程理论方法应用,1996(5):18-22.

[2]汪传旭.交通运输与经济协调发展的建模与应用研究[D].上海:上海交通大学,1997.

[3]武旭,胡思继,崔艳萍,等.铁路运输与社会经济协调发展评价问题的研究[J].铁道学报,2005(6):20-25.

[4]武旭,胡思继,崔艳萍,等.交通运输与经济协调发展评价的研究[J].北京交通大学学报,2005(6):10-14.

[5]杜志平,穆东.系统协调发展程度的DEA评价研究[J].运筹与管理,2005(2):75-81.

[6]曾珍香.可持续发展协调性分析[J].系统工程理论与实践,2002(3):18-21.

[7]查伟雄,熊桂林,刘会林,等.“交通运输—区域经济”复合系统的效率评价[J].系统工程,2007(5):60-65.

[8]谢艾国,罗英,王应明.时序DEA的理论与方法研究[J].系统工程与电子技术,1999(11):1-4.

[9]何静.只有输入(输出)的数据包络分析及其应用[J].系统工程学报,1995(2):48-55.

[10]Cooper W W,Seiford L M.Data Envelopment Analysis[M].Boston:Kluwe Academic Publishers,2000.